Навигация
Определение параметров объекта регулирования
1.2.3 Определение параметров объекта регулирования
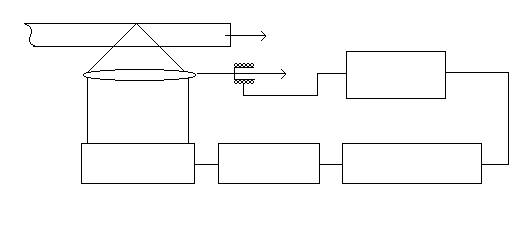
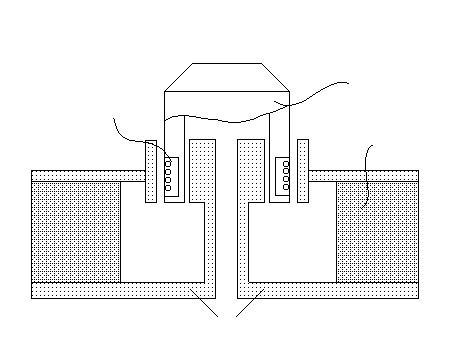
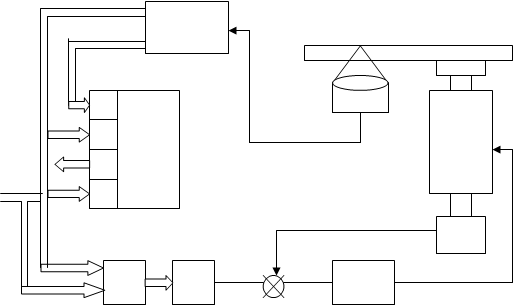
Основная цель, стоящая при разработке подвески, обеспечить движение головки только по жестко заданным направлениям. Подвески могут быть с помощью линейных подшипников механического или электромагнитного типа и пружинных гибких направляющих. В первом случае перемещение в направлении регулирования ничем не ограничивается, а в перпендикулярных направлениях предотвращается путем выбора соответствующих подшипников с минимально возможными допусками у механических и максимальной жесткостью у электромагнитных. Тогда с учетом демпфирования в подвесе и диссинации энергии в катушке, уравнения движения подвижной части имеют вид
![]()
Так как головка имеет пружинную подвеску, то ее движение описывается уравнением
![]()
![]()
где с - жесткость пружин,
![]() - коэффициент вязкого трения,
- коэффициент вязкого трения,
или в операторной форме:
![]()
где ![]() - постоянная времени пружинной подвески;
- постоянная времени пружинной подвески;
![]() - относительный коэффициент затухания;
- относительный коэффициент затухания;
![]() .
.
Плоские параллельные пружины, использующиеся в подвеске для системы фокусировки, должны иметь очень высокую жесткость при изгибе в направлении фокусирования жесткость должна быть мала.
Определяем постоянную пружинной подвески:
![]() =
=![]() = 7,071*10 - 3
= 7,071*10 - 3
Определяем относительный коэффициент затухания
![]() =
= ![]() = 0,011
= 0,011
Определяем коэффициент К:
К= 1/с = 1/200 = 0,005
Находим передаточную функцию объекта регулирования:
Wор (S) = Kор /![]() = 0,005 / 0,00005*S2 + 0,00015*S +1
= 0,005 / 0,00005*S2 + 0,00015*S +1
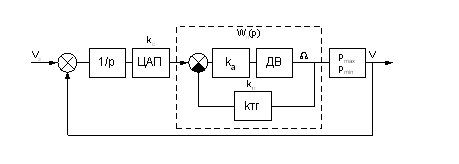
1.2.4 Определение передаточных функций разомкнутой и замкнутой систем
Находим передаточную функцию разомкнутой системы по формуле:
Wразомк. (S) = Wдп(S) * Wдв(S) * Wор(S) =
=(1,5*106*0,785*0,005)/ (10-6*S+1)(104*S+1)(0,00005*S2+10-4*S+1)=
= 5887,5/(0,00005*S2+10-4*S+1)
Находим передаточную функцию замкнутой системы по формуле:
Wзамк. (S) = Wразомк. (S) / (1 – Wразомк. (S)) =
= 5887,5/(0,00005*S2+10-4*S – 5886,5)
2. Синтез корректирующего устройства
При синтезе корректирующего устройства нужно исходить из того, что объект регулирования - неизменная часть, а синтезу подлежат корректирующие устройства или регулятор - изменяемая часть системы.
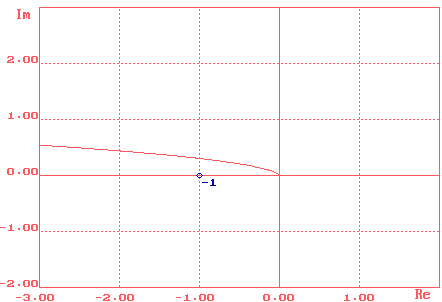
Рис.9. Годограф нескорректированной системы
При отсутствии корректирующего устройства КУ, то есть при Wку(s)=1, получены следующие характеристики:
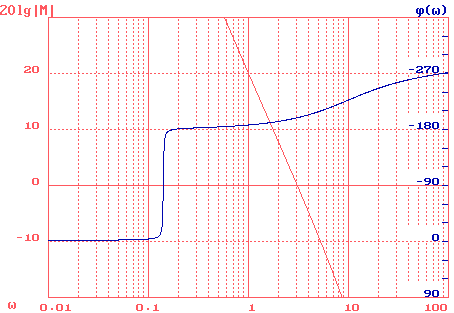
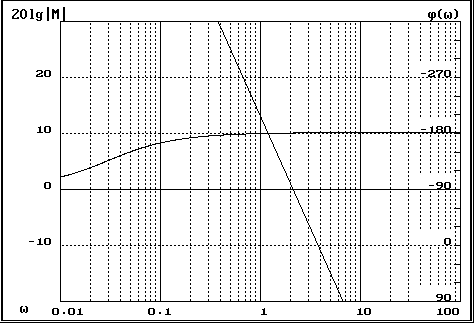
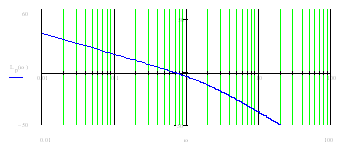
Рис.10. ЛАЧХ и ЛФЧХ нескорректированной системы
Приведённые выше характеристики были получены при общем коэффициенте усиления разомкнутой системы K, при котором должна обеспечиваться заданная точность xmax.
Так как данная система статическая , то общий коэффициент усиления разомкнутой системы определяется из соотношения:
![]()
При подстановке числовых значений получаем, что
К = 499
Об устойчивости системы можно судить по ее годографу (АФХ). В устойчивой системе кривая годографа не должна охватывать точку с координатами (-j, 0).
В данном случае полученная система неустойчива и поэтому производим расчет корректирующего устройства, используя частотный метод синтеза, основанный на построении желаемой ЛАХ.
После ввода корректирующего устройства были получены следующие характеристики:
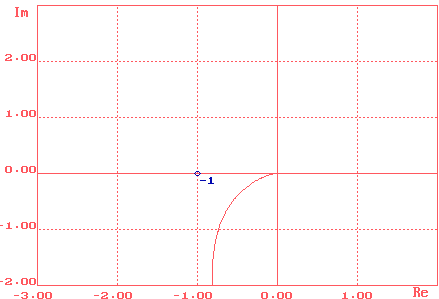
Рис.11. Годограф с КУ
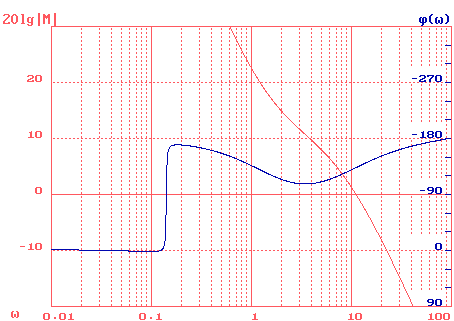
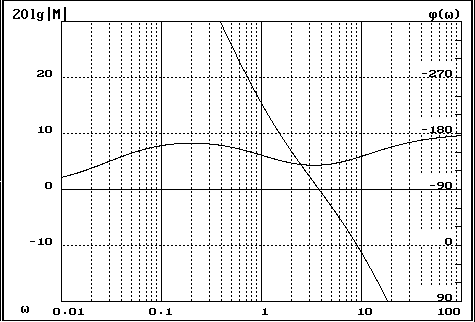
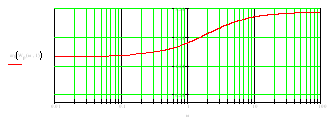
Рис.12. ЛАЧХ и ЛФЧХ с КУ
При построении характеристик (смотри рис.12) было произведено масштабирование по оси частот, то есть частота была уменьшена на три порядка (в 1000 раз).
Значит реальное корректирующее устройство имеет следующие параметры
w0 = 3090 (1/с).
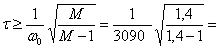 0,0006054 (сек.)
0,0006054 (сек.)
![]() = 0,0001009 (сек..)
= 0,0001009 (сек..)
запишем передаточную функцию реального КУ:
![]()
Определяем запас устойчивости по фазе и по амплитуде (см. рис.12.):
запас устойчивости по фазе на частоте среза c равен 57°, запас устойчивости по амплитуде равен , определяемый на частоте где j(w)=-180°, 7 дб.
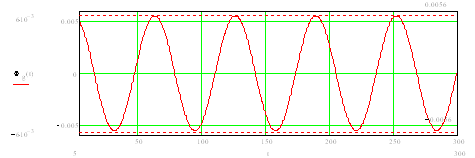
При задающем воздействии, равным единице (f (t) =1), процесс регулирования выглядит следующим образом (см. рис.13.).
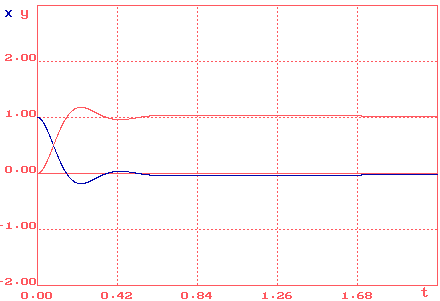
Рис.13. Процесс регулирования.
3. Заключение
В данной курсовой работе были выполнены следующие задачи:
· Построение характеристик (годограф, ЛАЧХ и ЛФЧХ) разомкнутой системы без корректирующего устройства и с корректирующим устройством;
· Расчёт передаточных функций отдельных звеньев и передаточных функций замкнутой и разомкнутой систем;
· Расчёт общего коэффициента усиления разомкнутой системы К;
· Расчёт корректирующего устройства, определение постоянных времени: Т и t ;
По результатам курсовой работы можно сделать следующие выводы:
· При введении корректирующего устройства разомкнутая система становится устойчивой, то есть годограф не охватывает точку с координатами (-j ; 0);
· Запас устойчивости по фазе и по амплитуде лежат в пределах нормы;
· Процесс регулирования при входном синусоидальном воздействии при заданных параметрах не возможен, но возможен при
g max= 1, x max= 2 мкм, w max = 20 (1/сек.)
4. Список литературы
1. Теория автоматического управления / Под ред. А.А.Воронова. - М. : Высшая школа. -1977.-Ч.I.-304с.
2. Бесекерский В.А., Попов Е.П. Теория автоматического регулирования. - М. : Наука, 1974.
3. Егоров К.В. Основы теории автоматического управления. – М. : Энергия 1967
Похожие работы
... которых действует в вертикальном, а другая в горизонтальном, по отношении к диску, направлениях. Называются они соответственно системой автоматического регулирования фокусировки (САРФ) и системой автоматического регулирования радиального положения пятна относительно дорожки записи (САРД). В видео дисковых системах дополнительно используется система управления в тангенциальном направлении (вдоль ...
... управления, одна из которых действует в вертикальном, а другая в горизонтальном, по отношении к диску, направлениях. Называются они соответственно системой автоматического регулирования фокусировки (САРФ) и системой автоматического регулирования радиального положения пятна относительно дорожки записи (САРД). В видео дисковых системах дополнительно используется система управления в тангенциальном ...
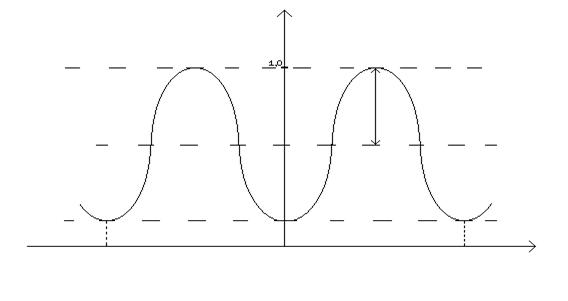
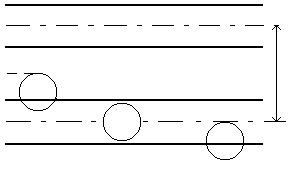
... информационной дорожки, причем величина ПС будет минимальной, если пятно находится на дорожке (в этом случае отражение света минимальное). Зависимость величины ПС сигнала от радиального положения пятна приведена на Рис.2.2. При , где n = 0, 1, 2, …, а q – расстояние между дорожками предполагается, что центр пятна совмещен с центральной линией дорожки. Относительный ...
... ); – Тангенциального слежения (САРТ); – Радиального слежения за дорожкой (САРД); – Радиального перемещения каретки (САРРП); – Вертикального слежения за фокусировкой (САРФ). 1. Система автоматического регулирования скорости вращения диска В оптических дисковых системах считывание информации с компакт-диска производится с постоянной скоростью. Для этого необходимо поддерживать линейную ...

0 комментариев