Методи визначення VaR та їх застосування

1.2 Методи визначення VaR та їх застосування

Існують три основних методи обчислення VaR:

1)  аналітичний метод (який інакше називають варіаційно-коваріаційним методом, або методом коваріаційних матриць);

2)  метод історичного моделювання (історичний метод, або метод історичних даних);

3)  метод статистичного моделювання (метод статистичних випробувань або, інакше, метод Монте-Карло) [15, c. 77].

Основна ідея аналітичного методу полягає у виявленні ринкових факторів, які впливають на вартість портфеля, і апроксимації вартості портфеля на основі цих факторів. Тобто фінансові інструменти, які становлять портфель, розбиваються, наскільки це можливо, на елементарні активи, такі, що зміна кожного залежить від впливу лише одного ринкового фактору.

Наприклад, багаторічна купонна облігація може розглядатися як набір безкупонних облігацій з різними строками погашення.

Портфель розкладається на базисні активи (компоненти), від яких залежить його поточна (сучасна) вартість (Present Value). Середньоквадратичне відхилення вартості портфеля визначається середньоквадратичними відхиленнями кожної з компонентів і матрицею коваріацій. Найбільш відоме втілення цієї моделі - Risk-Metrics J.Р. Morgan.

Цей метод вимагає тільки оцінки параметрів розподілу при явному допущенні про вид розподілу ринкових факторів. Звичайно роблять припущення про нормальний закон розподілу кожного ринкового фактору. На основі даних минулих періодів (далі історичних даних) обчислюються математичні очікування й дисперсії факторів, а також кореляції між ними. Якщо функція має лінійний вигляд, то розподіл прибутковості портфеля в цілому також буде нормальним, і, знаючи параметри розподілів ринкових факторів, можна визначити параметри розподілу всього портфеля.

Оцінивши стандартні відхилення логарифмів змін цін для кожного з вхідних у портфель активів, обчислюємо VaR для них шляхом множення стандартних відхилень на відповідному довірчому рівню коефіцієнт.

Повне обчислення VaR портфеля вимагає знання кореляційних зв'язків між його елементами.

Аналітичний метод може бути узагальнений на портфель з довільним числом різних активів - досить знати їх кореляції між ними. Кореляції важливі при розгляді нелінійних інструментів. Кореляції між різними активами особливо важливі при розгляді складних портфелів - саме кореляція визначає характер прибутків і збитків між різними інструментами.

Серйозна перевага цього методу полягає в тому, що для більшості ринкових факторів всі необхідні параметри нормального розподілу добре відомі. Відзначимо також, що оцінка ризику в рамках методології VaR, отримана за допомогою аналітичного методу, збігається з оцінкою ризику, пропонованою сучасною портфельною теорією [15, c. 79].

Аналітичний метод простий у реалізації і дозволяє відносно швидко (можливо, навіть у режимі реального часу) обчислювати VaR практично на будь-яких сучасних комп'ютерах. Але якість оцінки погіршується при збільшенні в портфелі частки інструментів з нелінійними функціями виплат.

Крім того, необхідність робити припущення про вид розподілів для базових активів є серйозними недоліками цього методу. Аналітичний метод володіє також рядом не менш істотних недоліків. Зокрема, доводиться опиратися на досить сумнівні гіпотези про нормальність розподілу і стаціонарність нормального розподілу, що робить метод мало придатним для сучасних ринкових умов.

Метод не застосовується для портфелів, які складаються з інструментів, вартість яких залежить від базисних активів нелінійним образом, наприклад, для портфелів, що містять нелінійні фінансові інструменти (опціони).

У кожному разі визначення VaR має на увазі знання функції розподілу прибутковості портфеля за обраний інтервал часу. Якщо стандартне відхилення як міра ризику визначає «ширину» щільності розподілу прибутковості портфеля, то VaR визначає конкретне значення втрат у вартості портфеля, що відповідає заданій вазі «хвоста» розподілу.

Приклад, що пояснює поняття й визначення VaR, наведений на рис.1.

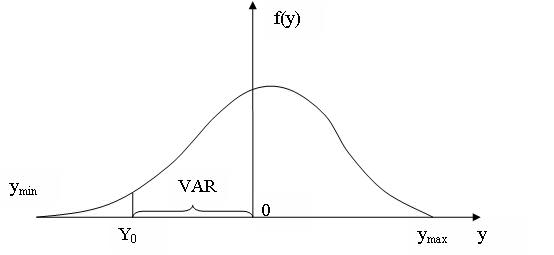
Рис.1. Типова функція VaR

По осі абсцис відкладені зміни цін ліквідації портфеля протягом певного періоду часу, по осі ординат - частота появи цих змін. Крива на малюнку задає щільність розподілу ймовірностей прибутків і втрат для даного портфеля і заданого періоду підтримки позицій. VaR-область відповідає обраному довірчому рівню 1-р = 98,5% у тому розумінні, що її площа становить 98,5% від загальної площі під кривою; відповідно площа області ліворуч становить 1,5% від загальної площі під кривою. Таким чином, VaR являє собою величину сумарних можливих втрат, які відповідають заданим довірчим рівням.

Резюмуючи все вищесказане по аналітичному методі, можна виділити основні позитивні й негативні сторони застосувань аналітичного методу для розрахунку VaR.

Його переваги:

1)  простота й наочність розрахунків;

2)  можливість розрахунку сукупної величини VaR для лінійних інструментів;

3)  доступність методичних матеріалів.

Недоліки:

1)  допущення про нормальний розподіл;

2)  неможливість розрахунку VaR для нелінійних інструментів [4, c. 181].

Найвідомішою реалізацією аналітичного методу є система RiskMetrics, розроблена банком J. P. Morgan. Як основне допущення передбачається, що зміни ринкових факторів ризику мають нормальний розподіл. Це припущення дозволяє визначити розподіл прибутків і збитків для всього портфеля, який також буде нормальним. Потім, знаючи властивості закону нормального розподілу можна легко обчислити збиток, який буде траплятися не частіше заданого відсотка випадків, тобто показник ризикової вартості.

Наріжним каменем аналітичного методу є процедура відображення ризиків (англ. risk mapping). Вона припускає декомпозицію кожного інструмента з портфеля на безліч більше простих, стандартних інструментів або позицій, при цьому кожна стандартна позиція повинна відображати лише один ринковий фактор ризику. Для кожної стандартної позиції визначається її поточна вартість як функція від єдиних ринкових факторів, за умови, що значення інших ринкових факторів ризику є фіксованими. Для оцінки опціонів використовується лінійна апроксимація, при цьому вартість опціону виражається у вигляді дельта-еквівалентної позиції «спот».

Таким чином, вихідний портфель фінансових інструментів представляється у вигляді еквівалентного портфеля стандартних позицій. Еквівалентність, яка у загальному випадку може бути лише приблизною, означає, що портфель стандартних позицій має таку ж чутливість до змін значень ринкових факторів. Величина ризикової вартості визначається саме для еквівалентного портфеля стандартних позицій. Подібна апроксимація дає гарні результати, якщо число стандартних позицій досить великий і портфель не містить великої частки опціонів і заснованих на них інструментів, для оцінки яких лінійна апроксимація може виявитися неадекватною [15, c. 83].

На наступному етапі робиться припущення, що одноденні процентні зміни або збільшення логарифмів значень факторів ризику мають нормальний розподіл з математичним очікуванням, рівним нулю. Для кожного ринкового фактору проводиться статистична оцінка величини середнього квадратичного відхилення, а також розраховуються коефіцієнти кореляції між різними парами факторів. Отримані результати використаються для визначення середніх квадратичних відхилень і коефіцієнтів кореляції для вартостей стандартних позицій. Середнє квадратичне відхилення стандартної позиції розраховується як добуток середнього квадратичного відхилення відповідного ринкового фактору на коефіцієнт еластичності вартості позиції за даним ринковим фактором (процентна зміна вартості позиції при зміні величини ринкового фактору на 1%). Коефіцієнти кореляції для стандартних позицій дорівнюють коефіцієнтам кореляції між відповідними ринковими факторами за винятком того, що коефіцієнт кореляції міняє знак, якщо вартість стандартної позиції змінюється назад стосовно зміни ринкового фактору [15, c. 88].

Потім складається коваріаційна матриця змін вартостей стандартних позицій. За допомогою цієї матриці і формули дисперсії для суми нормально розподілених випадкових змінних можна розрахувати дисперсію вартості портфеля, яка складається зі стандартних позицій. Коваріаційна матриця множиться зліва і справа на вектор значень вартостей позицій, у результаті чого обчислюється значення дисперсії портфеля, звідки шляхом витягу квадратного кореня отримується його середнє квадратичне відхилення.

Нарешті, на основі властивостей нормального розподілу визначається значення ризикової вартості. Так, якщо довірчий інтервал заданий на рівні 95%, те величина ризикової вартості дорівнює 1,65 стандартного відхилення портфеля. Таким чином, величина ризикової вартості розраховується за наступною формулою:

де Z - кількість середніх квадратических відхилень, яка відповідає заданому довірчому інтервалу; t - часовий обрій; p - вектор розміру позицій; Q - ковариационная матриця змін вартості позицій.

Метод історичного моделювання (historical simulation) є відносно простим підходом, який, на відміну від аналітичного методу, не опирається на теорію ймовірностей і вимагає відносно невеликого числа припущень щодо статистичних розподілів для ринкових факторів ризику. Як і в аналітичному методі, вартості інструментів портфеля повинні бути попередньо представлені як функції ринкових факторів ризику.

Шуканий розподіл прибутків і збитків отримується емпіричним шляхом. Поточний портфель піддається впливу реальних змін значень ринкових факторів ризику, які спостерігалися в минулому, наприклад, за останні n періодів. Для цього будується n безлічей гіпотетичних значень ринкових факторів на основі їхніх нинішніх значень і процентних змін за останні n періодів. Таким чином, отримані гіпотетичні значення грунтуються на реальних даних, але не тотожні їм. На основі цих гіпотетичних наборів значень ринкових факторів розраховується n гіпотетичних значень вартості портфеля. Порівняння цих значень з поточною вартістю портфеля дає можливість знайти n величин прибутків і збитків, викликаних зміною ринкових факторів. Отримані величини також є гіпотетичними, тому що портфель міг мати різний склад протягом останніх n періодів. Останнім етапом є побудова емпіричного розподілу ймовірностей прибутків і збитків, отриманих у результаті змін вартості портфеля, і визначення величини ризикової вартості [15, c. 90].

Метод статистичних випробувань Монте-Карло (Monte-Carlo simulation) також відноситься до методів імітаційного моделювання, і в чинність цього він має ряд загальних особливостей з методом історичного моделювання. Основна відмінність полягає в тому, що в методі Монте-Карло не проводиться моделювання з використанням реально спостережуваних значень ринкових факторів. Замість цього вибирається статистичний розподіл, який добре апроксимує зміни ринкових факторів, і проводиться оцінка його параметрів. Для цієї мети часто використається розподіл Стьюдента або суміш нормальних розподілів. Потім на основі обраного розподілу за допомогою генератора псевдовипадкових чисел генеруються тисячі або навіть десятки тисяч гіпотетичних наборів значень ринкових факторів. Отримані значення використовуються для розрахунку величин прибутків і збитків, викликаних зміною вартості портфеля. На останньому етапі будується розподіл прибутків і збитків портфеля й визначається величина ризикової вартості.

Вибір методу розрахунку показника ризикової вартості буде визначатися складом і структурою портфеля, доступністю статистичних даних і програмного забезпечення, обчислювальними потужностями й рядом інших факторів.

Аналітичний метод поступається методам імітаційного моделювання в надійності оцінки ризиків портфелів, які складаються з опціонів і заснованих на них інструментів, вартість яких залежить від ринкових факторів нелінійним образом, особливо на порівняно значних тимчасових горизонтах. Метод історичного моделювання концептуально простий і найбільш доступний для розуміння вищого керівництва, однак його реалізація вимагає наявності тимчасових рядів значень по всіх використовуваних у розрахунках ринкових факторах, що не завжди можливо для сильно диверсифікованих портфелів. Особливо це стосується даних по процентних ставках для валют країн, які не мають розвинених фінансових ринків. Крім того, історичне моделювання припускає, що поведінка ринку в минулому буде повторюватися і в майбутньому, що в загальному випадку невірно. Головними труднощами при реалізації методу Монте-Карло є вибір адекватного розподілу для кожного ринкового фактору й оцінка його параметрів. Крім того, оцінка ризиків великих диверсифікованих портфелів на основі методу Монте-Карло вимагає значних витрат часу й технічних ресурсів. Ще одна проблема полягає в тому, що гіпотетичні розподіли ймовірностей ринкових факторів, використовувані в аналітичному методі й методі Монте-Карло, можуть не відповідати реальності. Звичайно емпіричні розподіли змін ринкових факторів мають значний ексцес у порівнянні з нормальним розподілом, тобто випадки значних відхилень від середнього значення зустрічаються частіше, ніж це передбачено нормальним розподілом [4, c. 194].

Варто підкреслити, що керування ринковим ризиком не вичерпується наведеними вище процедурами. Зокрема, ризик-менеджер зобов'язаний звертати увагу на коректність обраної ним моделі ринку, на репрезентативність використовуваних даних і правильність статистичних гіпотез. Тому при керуванні ринковим ризиком дуже корисним представляється також апостеріорний аналіз. Наприклад, обчисливши VаR для заданого портфеля, необхідно потім простежити, чи дійсно перевищення втрат над цим VаR відбувається лише в заданому малому відсотку випадків. Невідповідність фактичного відсотка перевищень теоретичному повинне наводити на думку про корекцію моделі або процедур обчислення VаR. На терміновому ринку ММВБ подібні процедури аналізу фактичних ризиків застосовуються вже давно.

При управлінні ринковим ризиком не варто також забувати, що хоча межі застосування VаR досить широкі (наприклад, вже існують розробки по впровадженню концепції VаR у процес вимірювання кредитного ризику), він не є панацеєю від всіх лих. Зокрема, VаR не може захистити від ризиків, пов'язаних з коливаннями цін всередині періоду підтримки позицій (наприклад, протягом торговельної сесії). Крім того, застосування VаR обмежене при врахуванні рідкісних, але досить небезпечних подій (типу «чорного вівторка» або банківської кризи). У таких випадках поряд з VаR варто застосовувати й інші методи.

ІІ ЗАСТОСУВАННЯ КОВАРІАЦІЙНОГО МЕТОДУ РОЗРАХУНКУ VAR НА ПРИКЛАДІ ФОНДОВОЇ БІРЖІ ПФТС