Навигация
Министерство образования и науки Самарской области
Министерство имущественных отношений Самарской области
Государственное образовательное учреждение
среднего профессионального образования
Тольяттинский индустриально-педагогический колледж (ГОУ СПО ТИПК)
ПРАКТИЧЕСКИЕ РАБОТЫ
Дисциплина: Основы геодезии
Принял: преподаватель____
____________ Гусарова С.А.
подпись Ф.И, О.
«_______»
Выполнил:
студент группы С-271
_____________
«_______» 2008 г.
2008
ПРЕДИСЛОВИЕ
Для закрепления теоретических знаний и для приобретения необходимых практических умений учебной программой дисциплины «Основы геодезии» предусматриваются лабораторные и практические работы, которые проводятся после изучения соответствующей темы на лекционных занятиях.
Следует обратить внимание студента на то, что перед началом решения задач по каждой из тем Вы должны изучить соответствующие разделы из рекомендованного Вам учебника (учебного пособия) и/или материалы лекций.
Если работа сдана позже установленного срока, то она должна быть защищена на консультациях.
К данному пособию прилагается лист контроля, который заполняется преподавателем после выполнения каждой практической работы.
Работы должны выполняться аккуратно. За небрежность оценка может быть снижена.
В результате изучения дисциплины и выполнения данных лабораторных, практических работ студент должен
знать:
суть основных геодезических понятий,
типы и устройство основных геодезических приборов
уметь:
читать карту, определять по карте длины и ориентирные углы проектных линий;
Использовать мерный комплект для измерения длин линий, теодолит для измерения горизонтальных и вертикальных углов, нивелир для измерения превышений; по известным координатам определять положение проектной точки на местности в плане и по высоте инструментальными методами
ПРАКТИЧЕСКИЕ РАБОТЫ
Практическая работа №1. Решение задач на масштабы
Масштаб - это отношение длины линии на карте, плане (чертеже) Sp к длине горизонтального приложения соответствующей линии в натуре (на местности) Sm.
Численный масштаб - 1/ М, правильная дробь, у которой числитель равен 1, а знаменатель М показывает во сколько раз уменьшены линии местности по сравнению с планом.
Например, масштаб 1:10000 означает, что все линии местности уменьшены в 10000 раз, т.е. 1 см плана соответствует 10000 см на местности
или 1 см плана = 100 м на местности,
или 1 мм плана = 10 м на местности.
Следовательно, зная длину отрезка Sp плана по формуле Sm=Sp*M можно вычислить длину линии на местности или по формуле Sp= Sm:M определить длину отрезка на плане.
Например, длина линии на местности 252 м; масштаб плана 1:10000. Тогда длина линии на плане Бр=252м : 10000=0,0252м = 25,2мм.
И обратно, длина отрезка на плане равна 8,5 мм; масштаб плана 1:5000. Требуется определить длину линии местности. Она будет 8,5 мм * 5000 = 42,5м.
Задача №1 Вычислите длину линии на местности Sm, для данных, приведенных в таблице 1. Результаты запишите в соответствующую графу таблицы 1.
Таблица 1
| Масштаб карты | Длина отрезка на карте, мм | Длина линии на местности Sm,M | Масштаб карты | Длина отрезка на плане, мм | Длина линии на местности, м |
| 1:10000 | 62,5 | 1:1000 | |||
| 1:25000 | 20,2 | 1:500 | |||
| 1:5000 | 12,5 | 1:2000 | |||
| 1:50000 | 6,2 | 1:5000 |
Таблица 2
| Масштаб карты | Длина отрезка на карте, мм | Длина линии на местности Sm,M | Масштаб карты | Длина отрезка на плане, мм | Длина линии на местности, м |
| 1:2000 | 80,4 | 1:50000 | |||
| 1:5000 | 380,5 | 1:1000 | |||
| 1:10000 | 536 | 1:500 | |||
| 1:25000 | 625 | 1:2000 |
Часто в геодезической практике приходится определять масштабы аэроснимков. Для этого измеряют длину отрезка на аэроснимке и длину горизонтального проложения этой линии на местности. Затем, используя определение масштаба, вычисляют масштаб.
Например: длина отрезка на аэроснимке 2.21 см.; длина горизонтального проложения этой линии на местности 428,6 м.
Тогда, согласно определению:
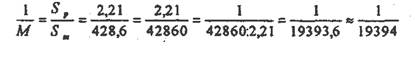
Задача №2 Определите масштабы аэроснимков, по данным приведенным в таблице 3. результаты записать в соответствующую графу таблицы 3
Таблица 3
| №п/п | Длина горизонтального приложения на местности м | Длина отрезка на аэроснимке | Отношение в соответствующих единицах | Масштаб аэроснимка |
| 1 | 625 м | 62,5 мм | 62,5 мм /625000мм | 1:10000 |
| 2 | 525 м | 5,25 см | ||
| 3 | 125,5 м | 2,51 см | ||
| 4 | 62,2 м | 31,1 см |
Точность масштаба
Длины линий на местности, соответствующие 0,1 мм карты (плана) называется точностью масштаба - tm. Это величина, характеризующая точность определения длин линий по карте (плану). Например: точность масштаба 1:25000 равна 2,5 м.
Расчет можно вести следующим образом:
в 1 см - 250м;
в 1 мм - 25 м;
в 0,1 мм-2,5 м
или to =0,1мм* 25000=2,5 м.
Задача №3
а) Определите точность масштабов:
1:10000 tm=
1:50000 tm=
1:1000 tm=
1:500 tm=
б) Точность масштаба карты (плана) равна:
tm1=0,5м; t2=0,05M; t3=____ ___; t4=_______;
Определите масштаб карты (плана).
1/М1=______; 1/М2=_______; 1 /МЗ=_______; 1/М4=_______;
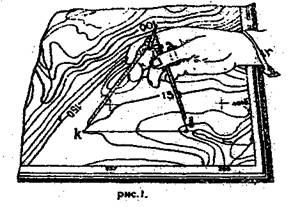
Задача №4 На карте масштаба 1:10000 (рис. 1) показан раствор измерителя, равный расстоянию между двумя точками карты KL. Используя приведенный ниже график линейного масштаба (рис.2), определите длины горизонтальных приложений линий местности для всех вариантов.
|
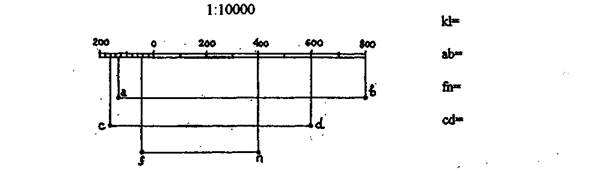
Задача №5 На графике поперечного масштаба (рис.3) с основанием равным 2 см., утолщенными линиями с номерами, обозначен раствор измерителя, равный расстоянию между двумя точками карты

Рисунок 3
Определите длины горизонтальных проложений линий местности для следующих вариантов:
| I вариант, масштаб 1:10000 | II вариант, масштаб 1:5000 |
| S1= | S1= |
| S2= | S2= |
| S5= | S5= |
| S= | S= |
| Ш вариант, масштаб 1:2000 S1= | IV вариант, масштаб 1: S1= |
| S2= | S2 = |
| S5= | S5 = |
| S= | S= |
Указание: в начале определите расстояния на местности (в соответствующем масштабе) для отрезков 0-2; а1в1; а2в2; аЗвЗ.
Задача №6 Постройте диаграмму масштаба 1:2000 на чертежной бумаге с основанием 2,5 см; число делений по основанию и по высоте принять равным 10 (n=m=10). Подпишите деления по основанию и высоте (через одно). Диаграмму приклеить, на оставленное ниже место.
Масштаб 1:2000
Практическая работа №2. Чтение топографического плана
Задача №1 Изучите условные знаки, имеющиеся на выданной Вам топографической карте, пользуясь таблицей условных знаков, в соответствии с их подразделением на 4-е группы: 1-я - контурныеусловные знаки;
2-я - внемасштабные условные знаки;
3-я - линейные условные знаки;
4-я - поясняющие условные знаки и надписи.
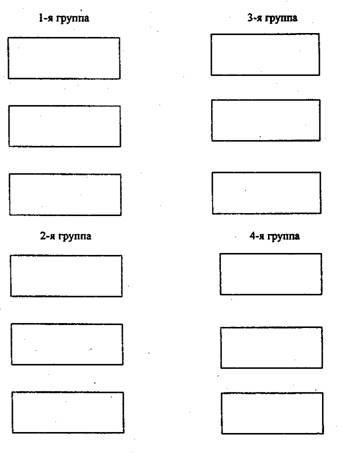
Выберите по 3 условных знака из каждой группы, скопируйте их, в отведенных для этого прямоугольниках, и подпишите рядом с прямоугольником названного условного знака.
Практическая работа №3. Чтение рельефа по плану (карте)
Задача №1 Изучите рельеф, представленный на Вашей карте горизонталями.
Найдите на карте пять основных форм рельефа. Скопируйте по каждой форме одну наиболее характерную. Подпишите в соответствии с правилами высоты горизонталей, поставьте скат штрихи. Проведите характерные линии рельефа (линии водотока и водораздела).
Основные формы рельефа.
| |

Практическая работа №4. Определение ориентирных углов линий по плану
Задача №1 На учебной топографической карте преподавателем кружками с наколами обозначены вершины замкнутой фигуры, называемой в геодезии полигон. Прочертить карандашом (по линейке) прямыми линиями стороны полигона. Составить, схематический чертеж полигона.
Пример составления схемы показан на рисунке 4
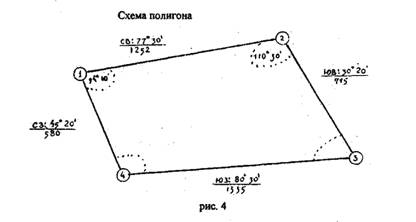
Рисунок 4
Задача №2 Измерить геодезическим транспортиром внутренние углы полигона, округляя отчеты до 5*.
Выписать результаты измерения углов на составленную Вами схему полигона, расположив надписи как указано на образце.
Вычислить практическую сумму измеренных углов:
∑β1=β1+……+β4
и теоретическую сумму углов по формуле ∑β0= 180(n-2), где n-число углов в полигоне.
![]() Вычислить разность ∑β1-β0=fβназываемую в геодезии невязкой.
Вычислить разность ∑β1-β0=fβназываемую в геодезии невязкой.
Сравнить полученную невязку с допустимой fβаiопределяемую по формуле: fβаi = l5√ n
Схема полигона.
Задача №3 С помощью геодезического транспортира измерить на учебной карте географический азимут и дирекционный угол стороны полигона 1-2. Вычислить азимут магнитный. Величину склонения магнитной стрелки рассчитать по данным карты.
Все измеренные и вычисленные величины показать на схематическом чертеже (образец составления схематического чертежа дан на рисунке 5
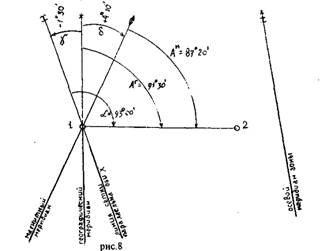
Рисунок 5
Указания к выполнению. Для измерения географического азимута надо через точку 1 провести географический меридиан. Если лист карты неполный, то надо параллельно перенести в т. 1 линию рамки (это истинный, географический меридиан). Точно так же перенести в т. 1 линию, параллельную координатной сетке.
Схематический чертеж.
Задача №4 Используя измеренные внутренние углы полигона и принимая дирекционный угол стороны 1-2 за исходный, вычислить последовательно дирекционные углы всех сторон полигона по формуле передачи дирекционного угла.
Li+1 =Li+l80-Вi., где В; - правый по ходу угол.
Вычисление дирекционных углов сторон полигона вести по ходу часовой стрелки. По значениям дирекционных углов вычислить румбы сторон полигона и выписать их значения на схематический чертеж полигона (см. образец, рис.6). Пример.
Первым дирекционным углом, подлежащим вычислению будет L2-3 .Тогда L2-3 = L1-2+180-B2 . Дирекционный угол линии 1-2 (см. рис.6) получили равный L1-2= 930 00', горизонтальный угол на т.2 (см. рис.5) получили равным В2= 110° 30', и графическая иллюстрация задачи имеет вид:
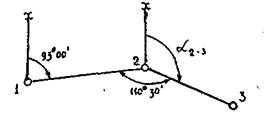
Следовательно,
L2-3=Ll-2+1800-B2=93000' + 180° - 110°30'= 162°30', а румб линии 2-3 – r 2-3=180°-162°30'=ЮВ: 17°30'

Замечание. Значение дирекционного угла линии 1-2, вычисленное последовательной передачей дирекционных углов, должно отличатся от значения измеренного дирекционного угла на величину, равную невязке углов в полигоне, т.е.
L1-2 выч. - L1-2 изм.= fB
Практическая работа №5. Определение прямоугольных координат точек
Задание №.1 Определить прямоугольные координаты всех вершин полигона, заданных на учебной топографической карте масштаба 1:10000 (1:25000).
Указания к выполнению.
Прямоугольные координаты точек определяют относительно километровой координатной сетки, представляющих собой систему линий, параллельных координатным осям зоны, образующих систему квадратов. Выходы линий координатной сетки (сторон квадратов) подписаны в рамке карты в километрах.
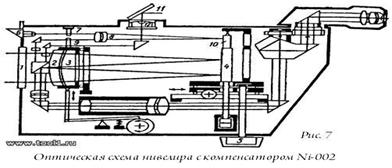
Порядок определения координат точки рассмотрим на конкретном примере. В данном случае это точка 1 (см. рис.7).
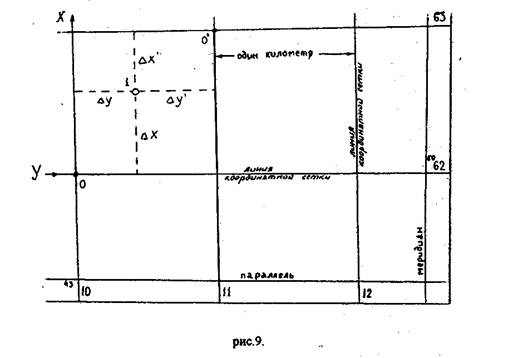
Рисунок 7
Координаты точки 1 (xi.yi) могут быть определены по формуле
х1= хo+ Δх
y1= у0 +Δу, где хо,уо координаты вершины квадрата, которые определяются по подписям выходов координатной сетки (в данном случае хо=6062км; у0 ==4310км)
или по формуле:
х1= х 'o+ Δх';
y1= у'о+ Δу'.
В данном примере прямоугольные координаты т. 1 равны
х1=6062km+720m=6065720m;
y1=4310км+501 м=4310501м.
или
х1=6063км-280м=6065720м;
yi=4311км-499м=4310501м.
При определении Вами координат точек, делайте схематический чертеж, иллюстрирующий положение точки относительно координатных осей.
Таблица 4
| Схематический чертеж Т.№1 | х0 = y0= Δх = Δy= х1= y1= |
| т.№2 | х0 = y0= Δх = Δy= х2= y2= |
| т.№3 | х0 = y0= Δх = Δy= х3= y3= |
| т.№4. | х0 = y0= Δх = Δy= х4= y4= |
Обратная геодезическая задача
Задание №2 По координатам вершин определить длины и дирекционные углы сторон полигона. Указания к выполнению: формулы для вычисления
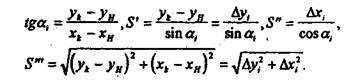
Вычисления вести в схеме для решения обратной геодезической задачи (таблица 5).
Схема для вычислений
Таблица 23
| Порядок решения | Обозначение величины | Значения величин | |||
| линия 1-2 | линия 2-3 | линия 3-4 | линия 4-1 | ||
| 1 | yk | ||||
| 2 | yH | ||||
| 3 | Δy | ||||
| 4 | хk | ||||
| 5 | хH | ||||
| 6 | Δх | ||||
| 7 | tga | ||||
| 8 | знаки Δх Δy | ||||
| 9 | r | ||||
| 10 | α | ||||
| 11 | sin r | ||||
| 12 | S' | ||||
| 13 | cos r | ||||
| 14 | S" | ||||
| 15 | Δx2 | ||||
| 16 | Δy2 | ||||
| 17 | Δх2+Δу2 | ||||
| 18 | S"' | ||||
| |
Практическая работа №6. Обработка линейных измерений
Измерение линий шагами, определение длины шага и составление таблицы перевода шагов в метры
Пример. На местности измерена лентой линия d=100 м. Эта же линия измерена шагами три раза: d1 = 140 шагов, d2 =144 шага и d3 =146 шагов.
Требуется: Определить длину I шага в метрах.
Решение 1. Определяем среднее арифметическое из количества шагов, равного 100 м; для этого
(140 + 144 + 146) / 3 = 143, 3 шага
2. Определяем длину шага /==100 м /143,3 шага = 0,70 м. Таблица примет следующий вид:
Задача №1 Определить длину / шага в метрах по приводимым ниже данным.
Таблица 6
| № задач | Дано | Решение | ||||
| d | d1 | d2 | d3 | среднее арифметическое из количества шагов | длина шага | |
| 1 | 150 | 202 | 208 | 207 | ||
| 2 | 175 | 307 | 315 | 310 | ||
| 3 | 200 | 390 | 397 | 400 | ||
| 4 | 100 | 188 | 186 | 186 | ||
| 5 | 100 | 191 | 193 | 192 | ||
Определение горизонтальной проекции линии по отметкам концов линии
Пример. Определить горизонтальную проекцию d линии АВ, если длина наклонной линии D= 100,00 м и отметки точек: НА = 120 ми НВ = 123 м (рис. 2).
Решение Вычисляем превышение к точки В над точкой А (рисунок 8 ). Как видно из рисунка h = 123 м -120 м = +3 м.

Рисунок 8
Определим поправку за наклон линии по формуле
∆h = h2 / 2D
где h - превышение;
D - длина наклонной линии.
Тогда
∆h = 32 / 2×100 = 0,045
Введя поправку в наклонную линию со знаком минус, получим горизонтальную проекцию 100,000 м - 0,045 м = 99,955 м.
Задача №2 Определить горизонтальную проекцию, а по следующим данным:
Таблица 7
| № задач | Дано | Решение | ||||
| НА | НВ | D | превышение h | поправка за наклон, ∆h | горизонтальная проекция, d | |
| 1 | 202,00 | 200,00 | 50,00 | |||
| 2 | 102,50 | 100,00 | 50,00 | |||
| 3 | 177,00 | 170,00 | 80,00 | |||
| 4 | 208,00 | 216,00 | 80,00 | |||
| 5 | 210,45 | 208,45 | 100,50 | |||
Определение наклонного расстояния по заданной горизонтальной проекции линии, если известны отметки концов линии
Пример. Определить наклонное расстояние D если горизонтальная проекция d = 100,00 м (рисунок 9), а разность отметок концов линии h=12 м.
tg ν = h / d = 12 / 100 = 0,12; ν = 6о 51'
D = h / sin ν = 12 / 0, 1193 = 100,6

Рисунок 9
или вводим поправку со знаком плюс к d по формуле
D = d + ∆h; ∆h = h2 / 2d
Задача №3 Определить наклонную длину D по следующим данным:
Таблица 8
| № задач | Дано | Решение | |||||
| h, м | d, м | tg ν | ν | D1 | ∆h | D2 | |
| 1 | 5,00 | 60,00 | |||||
| 2 | 6,45 | 81,50 | |||||
| 3 | 8,00 | 200,00 | |||||
| 4 | 3,00 | 100,00 | |||||
| 5 | 10,00 | 150,00 | |||||
| |
| |
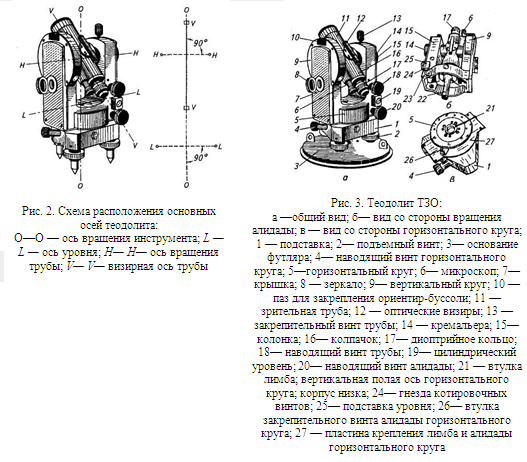
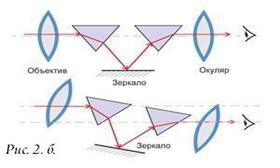
Теодолит — геодезический прибор, предназначенный для __________
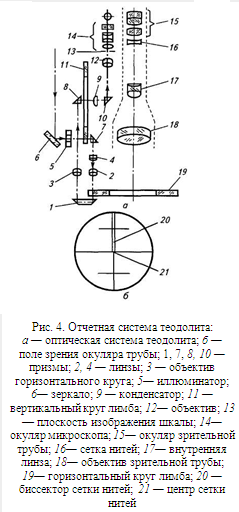
Задача №1 Изучите основные части, детали и оси теодолита. Напишите названия пронумерованных на рисунке 10 основных частей, деталей и осей теодолита.
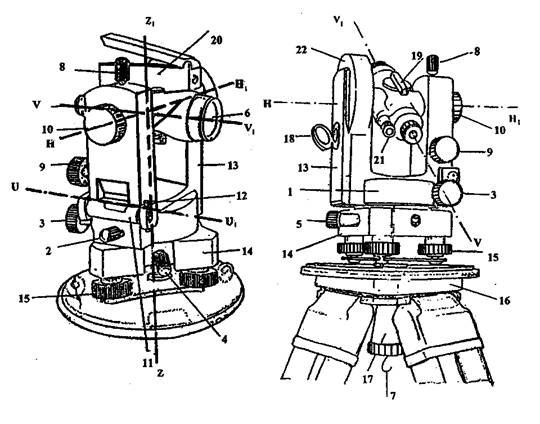
Рисунок 10
| 1 | 14 | |
| 2 | 15 | |
| 3 | 16 | |
| 4 | 17 | |
| 5 | 18 | |
| 6 | 19 | |
| 7 | 20 | |
| 8 | 21 | |
| 9 | 22 | |
| 10 | W W1 | |
| 11 | Z Z1 | |
| 12 | HH1 | |
| 13 | U U1 |
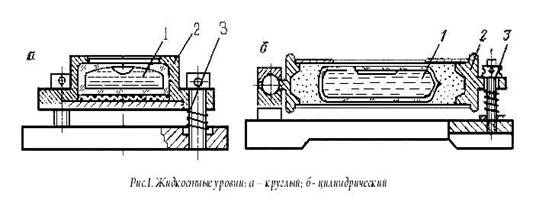
Задача № 2 Изучите устройство цилиндрического уровня и его свойства
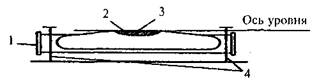
Рисунок 11
Напишите названия пронумерованных на рисунке 11 основных частей цилиндрического уровня.
1
2
3
4
Какое положение всегда стремится занять пузырек цилиндрического 'уровня?
Сформулируйте основное свойство осицилиндрического уровня.
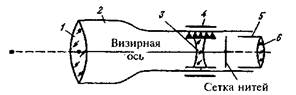
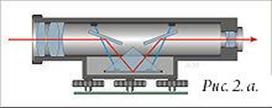
Рисунок12
Задача № 3 Изучите устройство зрительной трубы теодолита. На рисунке 12 дан схематический чертеж устройства зрительной трубы с внутренней фокусировкой в разрезе. Напишите названия пронумерованных частей.
| 1 | 4 |
| 2 | 5 |
| 3 | 6 |
Задача № 4 Напишите названия штрихов сетки нитей зрительной трубы в соответствии с номерами, указанными на рисунке13
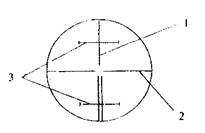
Рисунок13
| 1 |
| 2 |
| 3 |
Задача № 5. Изучите принцип работы отсчетного устройства теодолитов ТЗО; 2Т30.
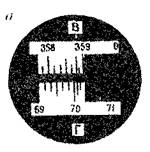
Рисунок 14 а
На рис. 14а показано поле зрения отсчетного микроскопа теодолита ТЗО. Выполните отсчеты по рисунку.
| Отсчет по: |
| Горизонтальному кругу |
| Вертикальному кругу |
| Отсчет по: горизонтальному кругу вертикальному кругу |
На рисунке 14 б дайте изображение штрихов лимбов для отсчета, наблюдаемого Вами в поле зрения штрихового микроскопа теодолита ТЗО. Запишите значения изображенных Вами отсчетов.
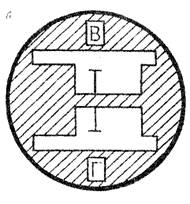
Рисунок 14 б
На рис. 15а, 156 показано поле зрения шкалового микроскопа теодолита 2Т30 при положительном (рис. 13,а) и отрицательном (рис. 13,6) углах наклона зрительной трубы.
| Отсчет по: |
| горизонтальному кругу_____________ |
| вертикальному кругу ___________ |
| горизонтальному кругу_____________ |
| вертикальному кругу ______________ |
Выполните отсчеты по рисунку.
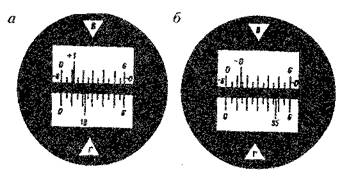
Рисунок 15
5.4 На рисунке16 а и 16 б дайте изображение штрихов лимбов для отсчета, наблюдаемого Вами в поле зрения шкалового микроскопа теодолита 2Т30. Запишите значения изображенных Вами отсчетов.
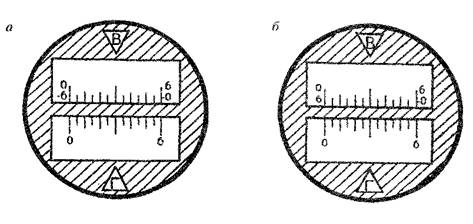
Рисунок 16
Отсчет по:
горизонтальному кругу горизонтальному кругу
вертикальному кругу вертикальному кругу
Начальные навыки работы с теодолитом
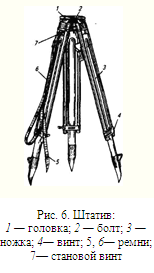
Задача № 6 Приведите теодолит в рабочее положение. В краткой форме изложите порядок действий при приведении теодолита в рабочее положение.
6.1 _________________
6.2. _________________
Задача № 7 Выполните пробные наведения зрительной трубы на цель. Изобразите на свободном поле (рисунок 17) правильное положение визирной цели в поле зрения трубы перед отсчетом.
Дайте названия винтов, которыми производили окончательное наведение зрительной трубы на цель.
а.
б.
в.
Поверки и юстировки теодолита
Задача № 8 Выполните поверки теодолита ТЗО (2Т30). Условия поверок и полученные результаты запишите в соответствующие графы тетради.
Первая поверка.
Условие: ________________
Результат:
Вторая поверка.
Условие:
Результат:
Третья поверка.
Условие:
Результат:
Четвертая поверка.
Условие:
Результат:
Лабораторная работа №2. Измерение горизонтальных углов
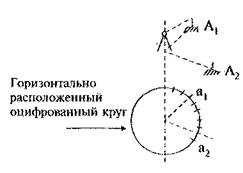
Рисунок 18
Задача № 1 Основываясь на принципе измерения горизонтального угла, покажите на рис.18 измеряемый угол и напишите формулу для его вычисления. Дайте определения величин а1, а2:
= --------------------------------------------------
а1= --------------------------------------------------
а2= --------------------------------------------------
Задача № 2 Измерьте заданный преподавателем горизонтальный угол полным приемом и запишите результаты измерений в журнал.
Журнал измерений горизонтальных углов
Теодолит № Дата
Наблюдал Погода
Записывал
| № точек стояния | № точек наблюдений | Отсчет по лимбу горизонтального круга | Значение углов из полуприемов | Среднее значение углов | |||
| о | , | о | , | о | , | ||
| 2 | 184 | 25 | 79 | 48 | |||
| 3 | 104 | 37 | |||||
| 1 | КП | 79 48,5 | Образец записи | ||||
| 1 л | 275 | 49 | 79 | 49 | |||
| 3 | 196 | 00 | |||||
Лабораторная работа №3 Измерение вертикальных углов
Задача 1 Дайте определения следующимвеличинам.
Угол наклона:
Место нуля вертикального круга:
Задача 12. Выполните измерения углов наклона по двум направлениям, заданным преподавателем. Результат запишите в журнал, используя формулы.
Теодолит ТЗО:
МО-= 1/2 (КП+КЛ-180°.);
۷ =КЛ- МО; ۷ =МО-КП+!80°.
Теодолит 2Т30:
МО=1/2 (КЛ+КП); ۷ =КЛ-МО; ۷ =МО-КП.
Вычислите по каждому направлению значения места нуля ж угла наклона.
Журнал измерений углов наклона
Теодолит________ № ________ Дата
Наблюдал______________ Погода
Записывал
| № точек стояния | № точек наблюдения | Отсчеты по вертикальному кругу | Место нуля | Угол наклона | |||||
| КЛ | КП | ||||||||
| о | , | о | о | , | о | , | |||
| 1 | Ферма | I | 26 | 178 | 14 | 359 | 50 | + 1 | 36 |
Лабораторная работа №4 Изучение нивелира
Геометрическое нивелирование является фактически основным методом определения превышений, которые используются при вычислении высот точек. Для выполнения геометрического нивелирования используется комплект приборов, в который входят нивелир, штатив и рейки с сантиметровыми делениями.
В результате выполнения данного задания Вы должны получить начальные навыки работы с нивелиром.
При выполнении задания Вы должны пользоваться рекомендованными преподавателем учебными пособиями и конспектом лекций.
Задача № 1 Дополните чертеж (рисунок19), показав:
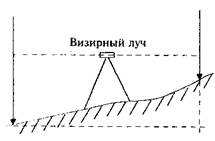
Рисунок19
| 1 Где определяемая величина 2 Какие величины необходимо определить, чтобы вычислить превышение |
3. Напишите формулу для определения превышения h =
Задача № 2 Закончите определение. Нивелир — геодезический прибор.
Сформулируйте основное геометрическое условие нивелира с цилиндрическим уровнем.
Задача № 3 Подпишите начало и конец в оцифровке черной и красной сторон, используемых Вами реек (рисунок 20).
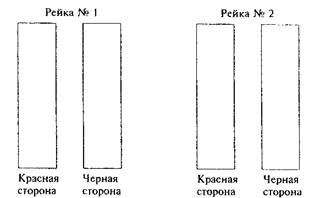
Рисунок 20
Задача № 4 Изучите основные части, детали и оси нивелира НЗ
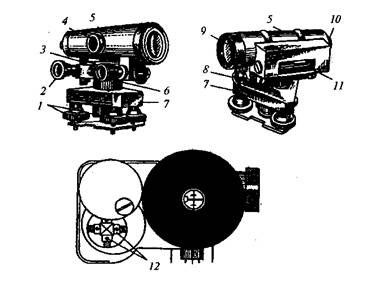
Рисунок 21
Напишите названия основных частей и деталей, пронумерованных на рисунке 21
| 1 | 7 |
| 2 | 8 |
| 3 | 9 |
| 4 | 10 |
| 5 | 11 |
| 6 | 12 |
Задача № 5 Укажите на рисунке 22 правильное положение пузырька контактного уровня перед отсчетом по рейке. Укажите, каким винтом надо действовать.
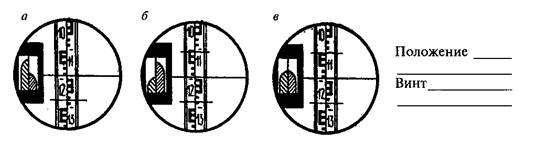
Рисунок 22
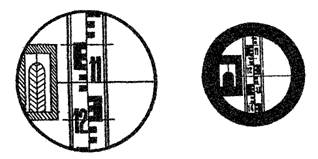
Рисунок 23
Задача № 6 На рисунке 23 показано поле зрения трубы нивелира. Произвести отсчет по нити для определения превышения.
Тема 2. Поверки и юстировки нивелира НЗ
Задача №7. Выполните поверки нивелира НЗ.
Нивелир НЗ № ______ , год выпуска
Первая поверка
Условие:
Результат:
Вторая поверка
Условие:
Результат:
Третья поверка (порядок выполнения условия проиллюстрируйте чертежом).
Условие:
Схематический чертеж
а.
6.
Результат:
Порядок исправления (юстировки):
Практическая работа №7 Обработка результатов нивелирования
Определение превышений на станции способом «из середины»
Задача № 8. Повторите порядок работы на станции при техническом нивелировании и определите превышения между точками, на которых установлены рейки. Результаты наблюдений запишите в журнал.
Журнал технического нивелирования
Нивелир_ №________ Дата_______________________
Наблюдал________________ Погода _______________________
Записывал____________
| станций | № нивелирных точек | Отсчеты по рейкам | Превышения | Средние значения превышений | Высоты | ||
| задней | передней | + | -' | ||||
| 1 | П.П. 21 | Образец записи | |||||
| 1460 (1)* | 1562 (2) | -102 (7) | -103 (9) | ||||
| xl | 6144 (4) | 6248 (3) | -104 (8) | ||||
| 4684 (5) | 4686 (6) | ||||||
| * Номера в скобках указывают порядок действий | |||||||
Задача № 9 Покажите на рисунке 22 цифрами порядок Ваших действий при проложении хода технического нивелирования для определения высот точек теодолитного хода
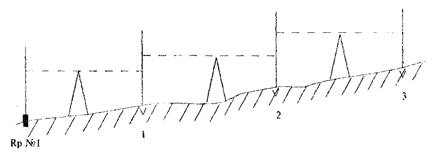
Рисунок 24
Задача N° 10 Выполните обработку страницы журнала технического нивелирования.
Журнал технического нивелирования
Нивелир № Дата
Наблюдал Погода
Записывал
| № станций | № нивелирных точек | Отсчеты по рейкам | Превышения | Средние значения превышений | ||
| задней | передней | + | - | |||
| 1 | Rpl | 1040 | 0666 | 0374 | 0372 | |
| 1 | 5820 | 5450 | 0370 | |||
| 4780 | 4784 | |||||
| 2 | 1 | 1660 | 1090 | |||
| 2 | 6445 | 5875 | ||||
| 4785 | 4785 | |||||
| 3 | 2 | |||||
| 3 | ||||||
| 4 | 3 | 1360 | 1140 | |||
| 4 | 6145 | 5928 | ||||
| 4785 | 4788 | |||||
| 5 | 4 | 0550 | 1555 | |||
| 5 | 5338 | 6338 | ||||
| 4788 | 4783 | |||||
| 6 | 5 | 1980 | 1115 | |||
| Rp10 | 6765 | 5895 | ||||
| 4785 | 4780 | |||||
Практическая работа №8 Вычислительная обработка теодолитного хода
Обработку полевых материалов начинают с проверки “Журнала измерения горизонтальных углов”, обработки линейных измерений и выписки данных в “Ведомость вычисления координат”. При этом значения углов округляют до десятых долей минут.
Рисунок 25
В ведомости последовательно выполняют описываемые ниже действия.
Вычисление угловой невязки
а). Подсчитывается сумма измеренных углов:
Sb изм = 899° 58¢ 1;
б). Определяется теоретическая сумма углов для замкнутого полигона по формуле
Sb теор = 180° (п - 2),
где п - число углов.
Если п = 7, то
Sb теор = 180° (7 - 2) = 900° 00¢ 0;
в). Полученная угловая невязка определяется по формуле
¦b = Sb изм - Sb теор
Например: ¦b =899° 58¢ 1 - 900° 00¢ 0 = -1¢9;
г). Допустимая угловая невязка определяется по формуле
¦b доп = ± 45² Ö`7 » ± 2¢0 ;
д). Сравнивается полученная и допустимая угловые невязки; если ¦b > ¦b доп, то производится повторное измерение углов ;
если ¦b < ¦b доп, например 1¢9 < 2¢0, или равны, то полученная невязка распределяется с обратным знаком поровну на все углы, образованные короткими сторонами.
Сумма поправок должна равняться величине полученной угловой невязки и быть противоположной ей по знаку.
Сумма исправленных углов должна равняться их теоретической сумме. Эти положения используются для контроля увязки углов.
Ориентирование полигона.
Величина дирекционного угла стороны I - II определяется по величине дирекционного угла исходной стороны А - I и величине примычного угла g по формуле
a I- II = a А-I + 180° - g,
Например, дирекционный угол исходной стороны a I- II = 295° 13¢ 0;
примычный угол g = 234° 13¢ 0.
Следовательно, дирекционный угол стороны хода I - II будет
a I- II = 295° 13¢ 0 + 180° - 234° 13¢ 0 = 241° 00¢ 0.
Вычисление дирекционных углов сторон полигона
Дирекционные углы других сторон полигона вычисляются по аналогичной формуле
a п = a п- I + 180° - bп,
где a п - дирекционный угол последующей стороны;
a п- I - дирекционный угол предыдущей стороны;
bп - исправленный, вправо по ходу лежащий угол между этими сторонами.
Это положение иллюстрируется схемой (Рисунок 26). Вычисления рекомендуется производить в следующем порядке:
| |
+180°
421° 00¢ 0
- 44° 45¢ 0
376° 15¢ 0
- 360°
16° 15¢ 0 . . . . a II- III
+180°
196° 15¢ 0
+360°
556° 15¢ 0
- 277° 16¢ 0
![]()
![]() 278° 59¢ 0 . . . . a III- IV
278° 59¢ 0 . . . . a III- IV
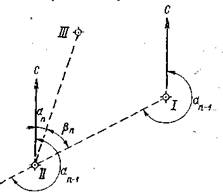
Рисунок 26
Если величина дирекционного угла оказывается более 360°, то следует 360° отбросить (376°15¢0 - 360° = 16°15¢0). Если же сумма дирекционного угла предыдущего и 180° окажется меньше внутреннего угла, вычитаемого из этой суммы, то следует к сумме прибавить 360° (196°15¢0 + 360° - 277°16¢0 = 278°59¢0).
Контроль вычисления дирекционных углов производится так. Если к дирекционному углу последней стороны прибавить 180° и вычесть величину внутреннего угла, расположенного между последней и первой стороной, то должен получиться дирекционный угол первой стороны:
210°47¢0 . . . . . . . . . . . a VII-I
+180°
390°47¢0
- 149°47¢0
241°00¢0 . . . . . . . . . . . a I-II
Перевод дирекционных углов в румбы.
Дирекционные углы переводят в румбы, пользуясь зависимостью между дирекционными углами и румбами
Зависимость между дирекционными углами и румбами| Величина дирекционного угла | Наименование румба | Величина румба |
| 0 - 90° | СВ | a |
| 90° -180° | ЮВ | 180°- a |
| 180° - 270° | ЮЗ | a - 180° |
| 270° - 360° | СЗ | 360° - a |
Например: a= 241°00¢0, т.е. сторона направлена между 180° и 270°; следовательно, румб будет назван - ЮЗ; а градусная величина его будет
241° - 180° = 61°
Горизонтальные проложения сторон выписываются в ведомость из абриса или соответствующего журнала с учетом поправок за компарирование и температуру .
Например, выписывают значения:
D I-II=102,50 м ;
DII-III=109,65 м и т.д.
Под итоговой чертой вычисляется сумма всех горизонтальных проложений – периметр полигона.
Например: ΣD=846,12 м.
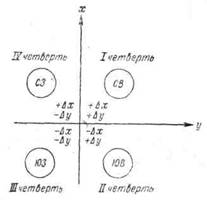
Рисунок 27
Вычисление приращений координат.
Знак приращения зависит от названия координатной четверти, в которой направлена данная сторона хода, и определяется по схеме (Рисунок 27.).
Например, для направления ЮЗ
Dх имеет знак минус (-)
Dу « « « (-)
Величины приращений находятся по “Таблицам приращений координат”, составленным на основе формул:
Dх = D cos a;
Dу = D sin a;
что видно из рисунка 28
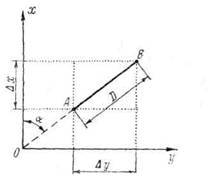
Рисунок 28
Приращения рекомендуется вычислять, пользуясь “Пятизначными таблицами натуральных значений sin и cos”, и калькулятором. В этом случае выбранные из таблиц значение sin и cos надо лишь перемножить на длину стороны.
Вычисленные приращения округляются до сантиметров и вписываются в графу “Приращения вычисленные”.
Например:
DX = - 49, 69;
DY = - 89, 65.
Определение линейной невязки.
Для этого сначала составляют суммы всех вычисленных приращений DX положительных (SDX+) и отрицательных (SDX-), а затем их алгебраическую сумму, которая для случая замкнутого полигона и будет величиной невязки по оси абсцисс.
¦х = S DX .
| Например: | |||
| +105,26 | |||
| +20, 23 | -49,69 | ||
| +93,83 | -135,58 | ||
| +59, 71 | -93,73 | ||
| S DX+ = +279,03 | S DX- = -279,00 | ||
| ¦х = (+279,03) + (-279,00) = +0,03 | |||
Аналогично действуют, вычисляя невязку по оси ординат
п
¦y = S DY ;
¦y = (+279,03) + (-273,50) = -0,27.
Абсолютная линейная невязка в периметре полигона определяется по формуле:
ƒD = √ (ƒх)2 + (ƒy)2
Например:
¦D = √ (0,03 )2 + (0,27)2 = ± 0, 28.
Относительная линейная невязка определяется отношением абсолютной невязки к периметру полигона.
¦D / SD = 0,28 / 846,12 » 1 / 3000,
где SD - периметр полигона.
Если полученная относительная линейная невязка не превышает 1/2000, то результаты считаются благополучными, и можно распределять невязки, полученные по осям координат.
Если ¦D / SD > 1 / 2000 , то необходимо тщательно проверить вычисления и при необходимости произвести повторные измерения.
Если ¦D / SD < 1 / 2000 , то производится распределение невязки ¦х и ¦y путем введения поправок в вычисленные приращения DC и DY пропорционально длинам сторон:
(¦x / SD)´Dn и (¦y / SD)´Dn
где Dn - длина горизонтального проложения соответствующей стороны.
Поправка вводится со знаком, обратным знаку невязки. Так как при этом поправка может выражаться лишь долями сантиметра, то надо ее округлить до целого сантиметра и вводить только в приращения, соответствующие наибольшим сторонам.
Если ¦x = 0,03, то поправки по 1 см. вводятся только в приращения, соответствующие лишь большим сторонам III - IV, V - VI, VI - VII.
Во всех случаях сумма поправок должна равняться величине полученной невязки, но с обратным знаком.
Исправленные (увязанные) приращения вычисляются как алгебраическая сумма вычисленных приращений и соответствующих поправок.
Например:
(DYI-II) испр = (-89,65) + (+0,03) = - 89,62
Контроль увязки приращений: в замкнутом полигоне алгебраическая сумма исправленных приращений по каждой оси должна равняться нулю.
Вычисление координат вершин полигона.
Координаты точки I заданы
ХI = 0,00; YI = 0,00.
Координаты последующих точек вычисляются по формулам:
Хn = Х n-1 + (DC) испр; Yn = Y n-1+ (DY) испр,
где
| Хn и Yn- | координаты последующих точек; |
| Х n-1 и Y n-1- | координаты предыдущих точек; |
| (DC) испр и (DY) испр - | исправленные приращения сторон между соответствующими точками |
Например:
ХIII = (-49,69) + (+105,26) = +55,57;
YIII = (-89,62) + (+ 30,71) = -58,91.
Если к координатам последней точки прибавить приращения по последней замыкающей стороне, то должны получиться координаты первой точки, что и будет контролем правильности вычисления координат вершин замкнутого теодолитного хода.
Например:
(+ 93,73) + (- 93,73) = 0,00;
(+ 55,80) + (- 55,80) = 0,00.
Ведомость вычисления координат вершин теодолитного хода
| № точек | Внутренние углы | Дирекционные углы | Румбы | Горизонтальные проложения сторон | Приращения | Координаты |
| ||||||||||||||||||||
| измеренные | поправка | исправленные | название | вычисленные | поправка | исправленные | ± x | ± y |
| ||||||||||||||||||
| ° | ' | ' | ° | ' | ° | ' | ± ∆ x | ± ∆ y | ± ∆ x | ± ∆ y | ± ∆ x | ± ∆ y |
| ||||||||||||||
| å βизм = | å D = | ||||||||||||||||||||||||||
| å βтеор = 180° ( n – 2 ) = | Абсолютная линейная невязка ¦D= Ö (¦x)2 + (¦y)2 = | ||||||||||||||||||||||||||
| Угловая невязка ¦β = | Относительная невязка | Относительная невязка допустимая = 1 / 2000 | |||||||||||||||||||||||||
| ¦D/ å D = | |||||||||||||||||||||||||||
| Угловая невязка допустимая (¦β )доп = ± 1,5 t Ö n = | |||||||||||||||||||||||||||
| |||||||||||||||||||||||||||
Практическая работа №9 Нанесение точек теодолитного хода на план
Пользуясь значениями вычисленных координат, следует нанести плановые точки на план масштаба 1:500. Для этого необходимо на чертежной или миллиметровой бумаге вычертить координатную сетку со сторонами квадратов 5 см и произвести соответствующую оцифровку координат на осях Х и У.Полученные на плане точки необходимо соединить прямыми линиями и надписать значения румбов и горизонтальных проложений сторон полигона.
Примечание 1. Координатную сетку нанести в тонких линиях зеленой или синей тушью. Точки соединить линиями толщиной 1—2 мм черной тушью или в карандаше. Диаметр точек теодолитного хода для М: 1:500 - 1,5 мм.
На план теодолитного хода М 1:500 накладываем контур здания 36×12 м (произвольно), два угла которого привязываем к плановым точкам ближайшей стороны полигона полярным способом.
Пользуясь поперечным масштабом, определяем координаты углов здания графическим способом.
Пример: координаты точек:
ХА=1,40м, УА =20,20 м.
Хд = 1,40м, Уд = 56,20 м.
Значения координат точек теодолитного хода т. 1 и т. 4 надо взять из ведомости вычисления координат:
Х1 = 0,00 м Х4 =—36,70 м.
У1 = 0,00 м У4 = 49,59 м.
Для определения длины стороны S1, решаем обратную геодезическую задачу, используя дирекционные углы направлений 1-А, 4-Д
,tg γ1 = ∆Х1 / ∆У1 S1 = ∆Х1 / cos γ1
Вычисляем приращения
∆Х1 = ХА —Х1 = 1.40—0,00= 1.40 м
∆У1 = У А—У1 = 20.20—0.00 = 20.20 м,
∆Х2 = Хд—Х4= 1,40—(—36.70) =38.10 м,
∆У2 = Уд —У4 = 56.20—49,59 = 6.61 «,
Дирекционные углы направлений 1-А и 4-Д соответственно равны
tg γ1-А = 20,20 /1,40 = 14,428 tg γ1-А =86º 02´
tg γ4-Д = 6,61 / 38,10 = 0,1735 tg γ4-Д = 9º 50´
Длины сторон 1,40
S1 = 1,40 / 0,06917 = 20,24 м
S2 = 38,10 / 0,98530 = 38,67
Вычисляем значения углов β 1 и β 2
угол β 1 = 90°- г4-1 – α 1
угол β 2 = г4-1 + α 2 , где α 1 и α 2 углы треугольников
α 1 = 90° - γ1-А = 3°58'
α 2 = γ4-Д = 9°50'
β 1 = 90° - 53°30' + 3°58' = 40°28'
β 2 = 53°30' + 9°50' - 63°20'
Вычисленные значения расстояний и углов используем для составления разбивочного чертежа.
5! = 20,24 м; β 1 = 40°28';
52 = 38,67 м; β 2 = 63°20'.
МАСШТАБ 1:500
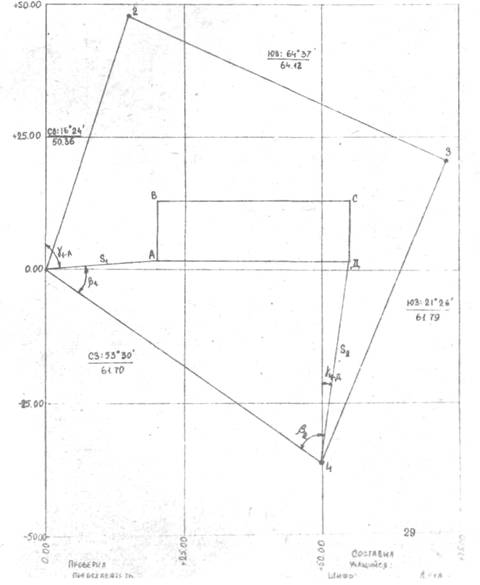
Рисунок 29 План теодолитного хода
Ведомость вычисления координат
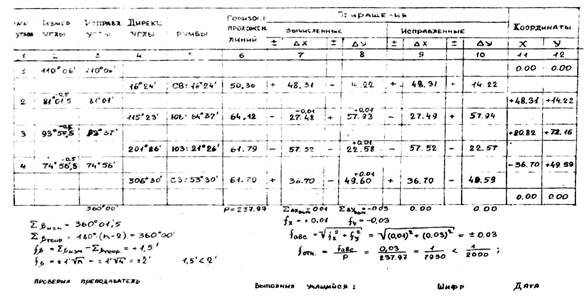
План теодолитного хода
Практическая работа №10 Подготовка топографической основы
Сущность работы состоит в следующем. Клиент заказал Вашей фирме выполнить вертикальную планировку части участка перед коттеджем в целях строительства теннисного корта и декоративного благоустройства участка. Площадь участка примерно равна 0,6 га.
Для разработки проекта вертикальной планировки требуется составить топографический план участка в масштабе 1:1000 (1:500) с высотой сечения рельефа 0,25 м (0,1 м).
Для этого Вашими коллегами при помощи теодолита и рулетки на местности была построена сетка квадратов со сторонами 20 м (рис. 30).
Аma-d = 330°30'
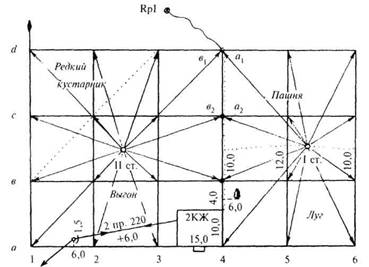
Рисунок 30
В вершинах квадратов забиты колышки вровень с землей и сторожки, на которых подписаны обозначения вершин по принципу обозначения клеток шахматной доски. Одновременно с разбивкой выполнялась и съемка элементов ситуации методом перпендикуляров. Для ориентирования линий плана был измерен магнитный азимут стороны а — d. Его значение Аma-d = 330°30'.
Затем произведено техническое нивелирование вершин квадратов с двух станций. Порядок нивелирования показан на рисунке 30. Все отсчеты записаны на полевой схеме (рис. 2) около вершин квадратов. На связующие точки, обведенные на рис. 2, 3 кружком, сделаны для контроля отсчеты с двух станций. Граница станций указана пунктиром (а1, а2, в1, в2). Контроль правильности связи (работ) станций выполняется по формуле: а1+в2=а2+в1, в общем случае суммы накрест лежащих отсчетов могут отличаться одна от другой не более чем на 5 мм. Передача высоты была выполнена на связующую точку d4.
Задача №1 Произвести обработку исполнительной полевой схемы нивелирования поверхности по квадратам (см. рис. 31), составить план участка в масштабе 1:1000. Выполнить интерполирование горизонталей при высоте сечения рельефа 0,25 м. Выполнить рисовку рельефа и вычертить план. Hd4 =
Исходная высота связующей точки d4 задается преподавателем (по усмотрению преподавателя может быть принят вариант передачи высоты на точку d4 нивелирным ходом от нивелирного репера).
Исполнительная полевая схема нивелирования поверхности
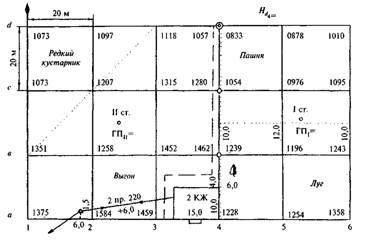
Рисунок 32
Контроль Съемку выполнил:
а1 + в2 - а2 + в1 = техник Медведев СМ.
а2 + в3 - а3 + в2 = Вычисления выполнил:
Вычисление горизонтов прибора.
ГПI =
ГПIII =
ГПIIII =
ГПIIIII = ГПсрII =
Пояснения к выполнению работ
Сделайте контроль нивелирования по связующим точкам.
Связующими точками являются точки в4, с4, d4 (см. рис. 32). В качестве примера сделайте контроль по связующим точкам в4 и d4. Отсчеты со станции I на связующие точки соответственно равны: а4=0833, а3=1239, а со станций II: в1=1057, в3=1462.
Тогда а1+в3=а3+в1. Имеем: 1462+083-1239+1057 = 1 мм, что допустимо. Результаты ваших контрольных вычислений запишите под рисунком 32.
Вычислите горизонт прибора и высоты вершин квадратов для станции I.
Горизонт прибора (ГП) вычисляется по формуле
ГП1 = Низв+ а0,
где Низв— известная высота точки, в Вашем случае — это высота связующей точки d4
а0 — отсчет по рейке на этой точке (в данном случае надо брать отсчет а1=0,833 м, полученный с первой станции, так как горизонт прибора определяется для станции I). Полученное значение горизонта прибора впишите на полевую схему в соответствующем месте. Затем по формуле
Hi = ГП1- аi
где Hi — высота вершин, определяемых для станции I;
ai — отсчет по рейке на этих вершинах (по черной стороне) вычислите высоты всех вершин в границах, определенных для станции I.
Последовательно получаемые значения высот запишите на полевую схему рядом с соответствующей вершиной квадрата.
3.Вычислите горизонт прибора и высоты остальных вершин для станции II.
Для контроля горизонта прибора вычислите его три раза (так как высоты трех связующих точек нами уже вычислены).
ГПII = Hd4 +в4; ГП′II= Нс4+в2; ГП′′II = Нв4+в3
Если расхождения между значениями ГП не превысят 5 мм, то вычисляют среднее значение и оно выписывается на полевую схему.
Высоты вершин в границе станции II вычисляются аналогично по формуле
Hi = ГПII-вi
и записываются у соответствующих вершин.
Составьте топографический план по результатам нивелирования по квадратам.
На листе чертежной бумаги в масштабе 1:1000 постройте сетку квадратов со сторонами 20 м и нанесите по промерам элементы ситуации. На план выпишите высоты всех точек (вершин), округляя значения до 0,01 м.
Путем интерполирования по сторонам квадратов найдите положение точек с высотами, кратными высоте сечения рельефа 0,25 м (используя как графический метод, так и интерполирование «на глаз»).
Точки с одинаковыми высотами соедините плавными кривыми-горизонталями.
Произведите «укладку» горизонталей и подпишите высоты горизонта лей, кратные 0,5 м.
Напоминаем! Высоты подписывают в разрывах горизонталей так, чтобы основание цифр было обращено вниз по скату.
Работу в карандаше предъявите преподавателю.
Похожие работы
... при проведении различных специальных маркшейдерских работ при разработке месторождений полезных ископаемых открытым способом. Вопрос: Опишите постоянные и временные маркшейдерские знаки и марки. Выполните необходимые рисунки Пункты геодезической основы в зависимости от их назначения и срока службы закрепляют постоянными или временными знаками. Временные знаки сохраняют только в процессе ...
ропашные, плодосменные или зернотравянопропашные, травянопропашные, пропашные, паропропашные, сидеральные универсальные специализированные: Зернопаровые, зернопаропропашные, зерновые, льняные, свекловичные, картофельные зернотравяные, плодосменные, пропашные, травянопропашные и др. Кормовые: прифермские Плодосменные, пропашные, травянопропашные, травянозерновые сенокосно- ...
... нивелиров с компенсаторами отличается от программы для уровенных нивелиров лишь тем, что в ней вместо пунктов г), е), и), и м), связанных с использованием цилиндрического уровня и элевационного винта, включены следующие поверки и исследования, связанные с наличием компенсатора: а) определение диапазона действия компенсатора; б) определение времени затухания колебаний маятника компенсатора; в) ...
... с качественной оценкой на основе материалов почвенных и других обследований. Учет проводят ежегодно по состоянию на 1 ноября. Регистрация землепользования является юридическим актом, закрепляющим на основе материалов по землеустройству право пользования конкретным земельным участком, представленным в постоянное или долгосрочное (свыше трех лет) пользование. Землепользования кроме указанной выше ...


0 комментариев