Навигация
Теперь можно перейти к непосредственному нахождению максимума функции f
2. Теперь можно перейти к непосредственному нахождению максимума функции f.
Поочерёдно подставляя координаты вершин многогранника в функцию f и сравнивать значения, находим что f(C)=f(4;1)=19 – максимум функции.
Такой подход вполне выгоден при малом количестве вершин. Но данная процедура может затянуться если вершин довольно много.
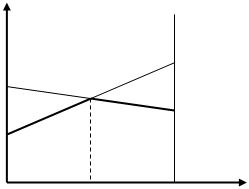
В таком случае удобнее рассмотреть линию уровня вида f=a. При монотонном увеличении числа a от -∞ до +∞ прямые f=a смещаются по вектору нормали[1]. Если при таком перемещении линии уровня существует некоторая точка X – первая общая точка области допустимых решений (многогранник ABCDE) и линии уровня, то f(X)- минимум f на множестве ABCDE. Если X- последняя точка пересечения линии уровня и множества ABCDE то f(X)- максимум на множестве допустимых решений. Если при а→-∞ прямая f=a пересекает множество допустимых решений, то min(f)= -∞. Если это происходит при а→+∞, то max(f)=+ ∞.
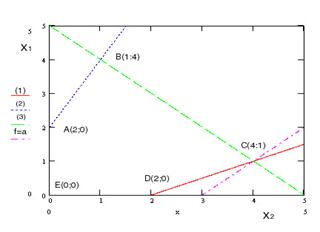
В нашем примере прямая f=a пересевает область ABCDE в точке С(4;1). Поскольку это последняя точка пересечения, max(f)=f(C)=f(4;1)=19.
2 этап.
Задача:
Решить графически систему неравенств. Найти угловые решения.
x1+ 2x2 <=10
2x1+x2 <=10
x1+3x2>=3
5x1-x2 >=-5
x1+6x2>=6
x1>= 0, x2>=0
> restart;
> ![]()
> ![]()
![]()
> ![]()
![]()
> ![]()
![]()
> ![]()
![]()
> ![]()
![]()
> ![]()
![]()
> ![]()
![]()
> ![]()
![]()
> ![]()
![]()
> ![]()
![]()
> ![]()
![]()
> ![]()
![]()
> with(plots);
> with(plottools);
> 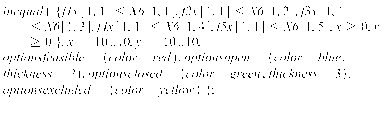
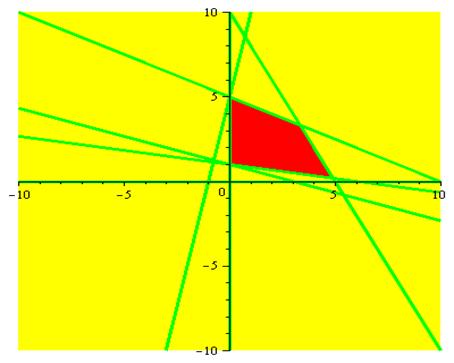
> S1:=solve( {f1x[1, 1] = X6[1, 1], f2x[1, 1] = X6[1, 2]}, [x, y]);
![]()
> ![]()
![]()
> ![]()
![]()
> ![]()
![]()
> ![]()
![]()
> ![]()
![]()
> ![]()
![]()
> ![]()
![]()
> ![]()
![]()
> ![]()
![]()
Ответ: Все точки Si где i=1..10 для которых x и y положительна.
Область, ограниченная данными точками: (54/11,2/11) (5/7,60/7) (0,5) (10/3, 10/3)
3 этап. Каждому ученику даётся один из 20 вариантов, в котором ученику предлагается самостоятельно решить неравенство графическим методом, а остальные примеры в качестве домашнего задания.
Занятие №4 Графическое решение задачи линейного программирования
Тип урока: урок изучения нового материала.
Вид урока: Лекция + урок решения задач.
Продолжительность: 2 часа.
Цели: 1) Изучить графическое решение задачи линейного программирования.
2) Научить пользоваться программой Maple при решении задачи линейного программирования.
2) Развить восприятие, мышление.
План занятия: 1 этап: изучение нового материала.
Похожие работы
... раскрываются более сложные понятия, как биржа или эффективность производства. Цель- дать основные понятия экономики в доступной младшим школьникам форме, заинтересовать ученика самостоятельно исследовать данные вопросы. 2.6 класс (2 полугодия - 1 урок в неделю): курс "Психология общения" - начальный курс общепсихологической подготовки. Цель - облегчить взаимодействие школьников между собой на ...
... и менеджмента Санкт-Петербургского Государственного технического университета соответствовал поставленной цели. Его результаты позволили автору разработать оптимальную методику преподавания темы: «Использование электронных таблиц для финансовых и других расчетов». Выполненная Соловьевым Е.А. дипломная работа, в частности разработанная теоретическая часть и план-конспект урока представляет ...
... . // Информатика и образование. -1994. - №4. 45. Подиновский В.В., Ногин В.Д. Паретооптимальные решения многокритериальных задач. - М.: Наука, 1982, - 256 с., ил. 46. Петросян Л.А., Зенкевич Н.А., Семина Е.А. Теория игр: Учебное пособие для университетов: / - М.: Высш. шк., Книжный дом "Университет", 1998. - 304с.: ил. 47. Программа курса информатики для начальной школы по ...
... образом, обращение с числовым рядом как с величиной позволяет по новому формировать сами навыки сложения-вычитания (а затем умножения-деления). Глава II. Методические рекомендации к изучению алгебраического материала в начальной школе 2.1 Обучение в начальной школе с точки зрения потребностей средней школы Как известно, при изучении математики в 5-м классе существенная часть времени ...




0 комментариев