Вычеркнем из матрицы М первую строку с закодированными состояниями. Получим матрицу М'

4. Вычеркнем из матрицы М первую строку с закодированными состояниями. Получим матрицу М'.

5. В начальной строке матрицы М' закодирован один элемент. Выберем из первой строки матрицы М' незакодированный элемент и обозначим его .

6. Построим матрицу M, выбрав из матрицы М' строки, содержащие у. Пусть В={₁,₂,...,_f,...,_F} - множество элементов из матрицы My, которые уже закодированы. Их коды обозначим через К₁,К₂,...,К_f,...,К_F соответственно.

7. Для каждого Кg_f (f=1, 2,...,F) найдем C¹_gf- множество кодов, отстоящих от Кg_f на расстояние Хэмминга, равное 1 и еще не занятых для кодирования состояний автомата. Построим множество .

Если D¹_ =0, то строим новое множество , где  - множество кодов, у которых кодовое расстояние с кодом K_f равно 2. Если и D²_ =0, строим D³_ и т.д., пока не найдем . Пусть .

8. Для каждого К_g находим w_gf=|K_g- K_f|² - расстояние Хэмминга между К_g и всеми используемыми кодами K_f(f=1, 2, ...,F).

9. Находим

10. Из  выбираем К_, у которого W_g=W_gmin. Элемент у кодируем кодом К_.

11. Из матрицы М' вычеркиваем строки, в которых оба элемента закодированы, в результате чего получаем новую матрицу, которую также обозначаем М’. Если в матрице М' не осталось ни одной строки, переходим к п. 12, иначе к п. 5.

12. Вычисляем функцию  где t_ij=|K_j-K_j|².

13. Конец.

Оценкой качества кодирования по рассмотренному алгоритму может служить число K=W/P, где P - число переходов в автомате. Очевидно, что K>=1, причем, чем меньше значение K, тем лучше результат кодирования.

Рассмотрим пример кодирования автомата, заданного таблицей переходов и выходов.

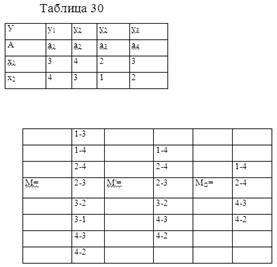
1. Строим матрицу М:

Кодируем первую строку: K₁=00;K₂=01;

2. Вычеркиваем из матрицы М 1-ю строку (1-3) и 6-ю строку (3-1). Получаем матрицу М', в первой строке которой незакодирован элемент 4. Обозначим =4 и запишем матрицу M_,. В матрице M_ закодированы 1 и З: В_={1,3}={00,01}  Находим W:

W₁₀=|00| |10|=3; W₁₁=|00| |11|=3;

|10|+|01|  |11|+|01|

Выбираем K₄=10.

Вычеркнем из М' строку (1-4). Получим новую матрицу М', в первой строке которой не закодирован элемент 2. Обозначим g=2 и запишем матрицу М₂. В матрице М₂ закодированы элементы 3, 4:

Вg={3,4}={01,10}

Вычислим K=W/P=9/8=1,125.

 

 

6. Обеспечение устойчивости функционирования цифровых автоматов. Гонки в автоматах

Одна из главных задач, решаемых на этапе структурного синтеза синхронных цифровых автоматов с памятью, заключается в обеспечении устойчивости их функционирования. Понятие устойчивости связано с разработкой такой принципиальной электрической схемы автомата, которая обеспечивала бы его функционирование в соответствии с таблицей переходов и выходов автомата.

Неправильное функционирование автомата (неустойчивая его работа) связано с особенностями физической реализации логических элементов и элементов памяти его схемы, а также различными величинами задержек распространения сигнала в элементах и комбинационных схемах.

Рассмотрим процесс обеспечения устойчивости функционирования автомата более подробно. После поступления очередного входного сигнала и формирования сигналов возбуждения на входах элементов памяти автомат переходит в новое состояние. При этом происходит формирование новых сигналов возбуждения по цепям обратных связей (с выходов элементов памяти через логические элементы на входы элементов памяти), и автомат переходит в новое состояние и т. д.

Таким образом, автомат, в общем случае, не может остановиться в каком-то определенном состоянии и начинает функционировать в режиме генератора состояний. Для устранения такого эффекта используют синхросерию — последовательность специальных (обычно прямоугольных) сигналов, подаваемых на входы элементов памяти и разрешающих поступление очередных сигналов возбуждения на входы элементов памяти только с приходом очередного синхросигнала. При отсутствии синхросигнала сигнал возбуждения не поступает на вход элемента памяти, и элемент памяти цифрового автомата не переключается, т. е. остается в каком-то состоянии.

Практически подключение синхросерии осуществляется к специальным входам элемента памяти, обозначаемым символом C на рисунках и называемым синхровходами. Введение синхросерии, однако, не обеспечит устойчивого функционирования автомата, если не учитывать некоторые особенности. Если при переходе из одного состояния в другое должны изменять свои состояния сразу несколько элементов памяти, то между ними начинаются состязания. Тот элемент, который выиграет состязания, по цепям обратной связи может изменить сигналы на входах других элементов памяти до того, как они изменят свои состояния. Это может привести к переходу автомата в состояние, не предусмотренное графом.

Если в процессе перехода из состояния а_m в состояние а_s под действием входного сигнала x_i автомат может оказаться в некотором промежуточном состоянии (а_i, а_k) в зависимости от того, какой из элементов памяти выиграл состязания, но, затем, при этом же входном сигнале перейдет в состояние а_s, то такие состязания называются допустимыми, или не критическими. Но если произойдет переход в состояние а_k (не предусмотренное графом переходов автомата) и правильность работы автомата нарушается, то такие состязания называются недопустимыми (критическими) или гонками. Пусть автомат должен выполнить переходы, изображенные на рис. 8.

Рисунок 8

Возможны следующие ситуации:

а) если очередной синхросигнал на входы элементов памяти автомата поступает раньше, чем кончились переходные процессы в его комбинационной схеме возбуждения и элементах памяти после поступления входного сигнала х_i, то возможно неправильное формирование сигнала возбуждения на входе одного или нескольких элементов памяти автомата, т. е. автомат может вместо перехода из состояния а_m в состояние а_s по входному сигналу x_i осуществить ложный переход в некоторое состояние а_t по тому же самому входному сигналу x_i;

б) если длительность входного сигнала х_i превышает длительность перехода автомата из состояния а_m в состояние а_s, то автомат может (при поступлении очередного синхросигнала) проскочить состояние а_s и попасть сразу в состояние а_k за счет двойного срабатывания автомата по входному сигналу х_i. Иными словами, состояние а_s может оказаться неустойчивым.

6.1 Методы устранения гонок в автоматах

Для обеспечения устойчивого функционирования автомата нужно разнести во времени момент подачи информации на входы его элементов памяти и момент снятия информации с выходов элементов памяти. При таком разнесении формирование очередного сигнала возбуждения любого элемента памяти в момент появления синхросигнала осуществляется только по значениям состояний элементов памяти в предшествующий момент времени, а переходные процессы в элементах памяти не влияют на формирование сигнала возбуждения (выходы элементов памяти отключены).

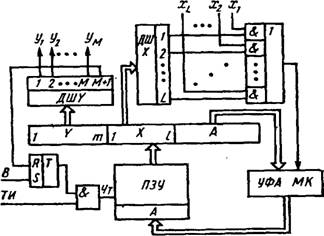
Естественно, что период следования синхросигналов при этом должен выбираться исходя из учета окончания переходных процессов, связанных с задержками распространения входного для автомата сигнала по логическим элементам комбинационной схемы возбуждения. В результате устойчивость функционирования цифрового автомата может быть обеспечена, например, использованием двухэтажной памяти. В этом случае каждый элемент памяти дублируется, и перепись информации из нижнего элемента памяти в верхний осуществляется по отсутствию синхросигнала (рис. 9.).

Сигналы обратных связей, используемые для формирования функций возбуждения, и сигналы выходов автомата снимаются с выходов элемента памяти верхнего яруса. При такой организации памяти автомата отсутствует опасность формирования повторного сигнала возбуждения по одному и тому же синхросигналу и перехода автомата в новое состояние. Последнее связано с тем, что переход в рабочее состояние автомата завершается после окончания действия синхросигнала.

Однако использование двойной памяти автомата приводит к замедлению работы автомата. Если обычно период синхросигналов выбирается из расчета, что сигнал возбуждения элемента памяти успеет пройти по самой длинной цепочке логических элементов и переключить элемент памяти, то здесь период нужно удлинить по крайней мере на 3t где t- задержка распространения сигнала в логическом элементе (1t- на инвертор и 2t - на второй элемент памяти).

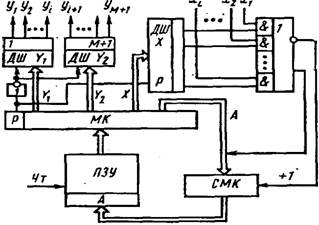
В случаях, когда из соображений быстродействия двухэтажную память использовать нельзя, прибегают к многофазной системе тактирования входных сигналов автомата. Так, для случая двухфазной синхронизации синхросериями CC1 и CC2 вместо одного входного сигнала x_i, (рис. 8) используются два разных: х_i • СС1 и x_i • СС2 (рис. 10).

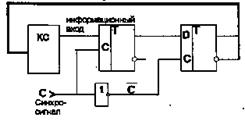
Рисунок 9

Рисунок 10

Таким способом устойчивость функционирования автомата обеспечивается автоматически. При двухфазной синхронизации необходимо, чтобы все дуги графа переходов автомата можно было бы разметить символами CC1 иCC2 так, что для любой вершины графа все выходящие из нее дуги отмечались бы символом одной синхросерии (например, СС1, а все дуги, заходящие в ту же вершину графа переходов автомата,— символом другой синхросерии (например, СС2). Если граф переходов автомата содержит контур нечетной длины, то такая разметка невозможна.

Однако ее можно сделать, преобразовав контур нечетной длины в контур четной длины, добавив дополнительную вершину или состояние автомата с пустым выходным сигналом. Задача преобразования произвольного графа с нечетными контурами к графу с четными контурами решается методами теории графов, в частности с использованием понятия цикпоматического числа графа и метода построения матрицы фундаментальных циклов графа.

Кроме описанных выше случаев, устойчивость функционирования цифрового автомата с памятью может быть частично обеспечена с помощью специальных мер, принятых относительно устранения в схеме автомата эффекта гонок. Это связано с тем, что элементы памяти имеют различные времена срабатывания. Различны также задержки сигналов возбуждения, поступающих на входы элементов памяти по цепочкам логических элементов различной длины.

Если при переходе автомата из одного состояния в другое, должны переключиться сразу несколько элементов памяти, то между ними начинаются гонки, (состязания), что может привести к неправильной работе автомата. В самом деле, при переходе автомата из состояния a_i; в состояние a_j на некоторый, хотя и очень короткий, промежуток времени может возникнуть промежуточное состояние автомата, отличное от a_i и a_j. Например, при переходе из a_i (0110) в a_j (1010) изменяют свое состояние два первых элемента памяти. Из-за состязаний может возникнуть состояние 1110 (или 0010), которое может привести к изменению состояния третьего или четвертого элемента памяти.

В последнем случае после окончания переходных процессов автомат уже не попадает в состояние a_j. При использовании двухэтажной памяти гонки в автомате не возникают, так как изменение состояния автомата происходит в то время, когда синхросигнал отсутствует.

Следует заметить, что современная элементная база включает в себя элементы памяти с уже встроенной двухэтажной памятью (например, JK-триггер). Существует еще один способ устранения гонок в автоматах, связанный со специальным кодированием состояний автомата, которое называется противогоночным кодированием.

Частным случаем противогоночного кодирования является соседнее кодирование, при котором состояния автомата, связанные дугой на графе переходов, кодируются двоичными векторами, отличающимися друг от друга только в одном разряде. Для проведения соседнего кодирования в графе переходов автомата не должно быть контуров нечетной длины. Примеры графов переходов автоматов, состояния которых закодированы соседним образом, представлены на рис.

Отметим, что проблема состязаний и некоторые другие вопросы обеспечения устойчивости работы автоматов возникли лишь с появлением потенциальной элементной базы. Используемая ранее (в ЭВМ второго поколения) импульсно-потенциальная элементная база предусматривала применение статических триггеров со встроенной задержкой.

При этом величина задержки выбиралась большей длительности импульсного сигнала, поступающего на вход триггера. Тем самым переходные процессы формирования сигналов на выходах элементов памяти автомата начинались лишь после окончания входного импульсного сигнала и, следовательно, не оказывали воздействие на входы этих же элементов памяти по цепям обратной связи. Нечто подобное осуществляется теперь в потенциальной элементной базе введением не совпадающих во времени серий синхронизирующих сигналов, в особенности при организации двухэтажной памяти.

Вывод

 

В процессе выполнения курсовой работы мы ознакомились с:

- основными понятиями структурных автоматов; - каноническим методом структурного синтеза автоматов; - теоремой Глушкова о структурной полноте; - основными этапами канонического метода структурного синтеза; - примерами канонического метода структурного синтеза; - кодированием состояний и выходов автомата и сложностью комбинационных схем; - обеспечением устойчивости функционирования цифровых автоматов; - гонкой в автоматах; - методами устранения гонок в автоматах.

Литература

1. Самофалов К.Г., Романкевич А.М., и др. Прикладная теория цифровых автоматов. - Киев. “Вища школа” 1987.

2. Соловьев Г.Н. Арифметические устройства ЭВМ. - М. “Энергия”. 1978.

3. Савельев А.Я. Прикладная теория цифровых автоматов - М. “Высшая школа”. 1987.

4. Каган Б.М. Электронные вычислительные машины и системы. - М. Энергоатомиздат. 1985.

5. Лысиков Б.Г. Арифметические и логические основы цифровых автоматов. - Минск. “Вышэйшая школа”. 1980.