Контрольная работа по электротехнике
“Расчёт цепей на переходные процессы”
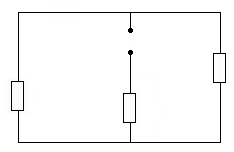
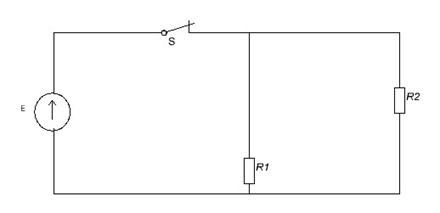
Задача 1
Дано:
R1=R2=R3=1Oм
I=1A
L=1Гн
Найти:
iL (t)=?
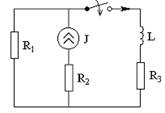
Решение:
1) До коммутации:
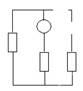
il(0-) = 0
2) Установившийся режим:
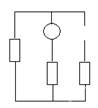
il(уст) = ![]()
3) Переходной процесс:
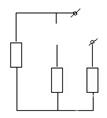
Rэкв = 2 Ом
il(t) = il(уст) + il(своб)
il(своб) = Aept
p = ![]() ;
; ![]()
il(0) = il(уст) + A
il(0-) = il(0)
![]()
4) ![]()
Ответ: ![]()
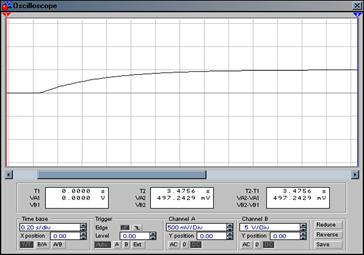
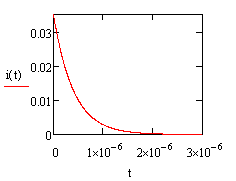
Рис. 1 - График
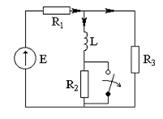
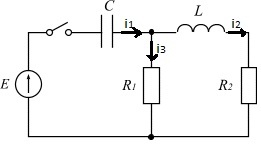
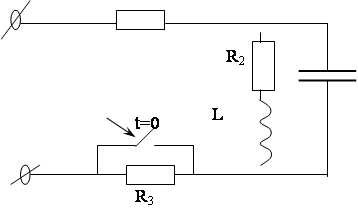
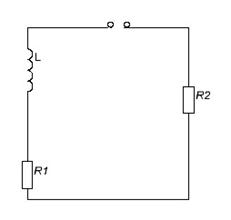
Задача 2
Дано: R1 = R2 = R3 =1 Ом
L = 1Гн
E = 10B
Найти: i2(t) -?
Решение:
1) До коммутации:
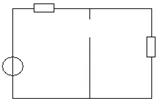
il(0-) = 10 А
i2(0-) = 0 А
2) Установившийся режим:
3)
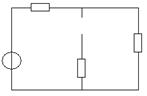
il(уст) = ![]()
![]()
4) Переходной процесс:
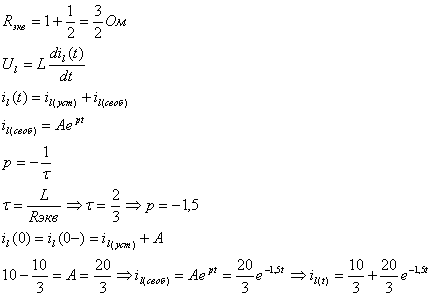

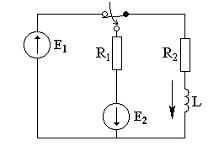
Ответ: ![]()

Рис. 2 - График
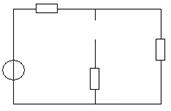
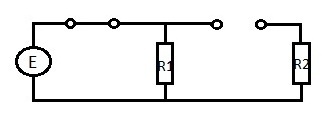
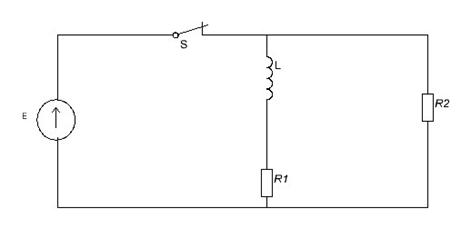
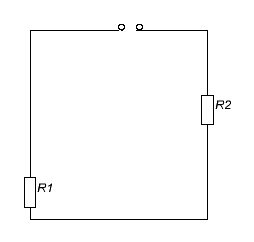
Задача 3
Дано: E1 = 100 B
E2 = 50 B
R1 = R2 = 10 Ом
L = 1 мГн
Найти: UL(t) – ?
Решение:
1) До коммутации:
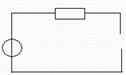
iL(0-) = 10A
2) Установившийся режим:
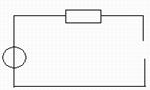
![]()
3) Переходной процесс:

Ответ: ![]()
Рис. 3 - График
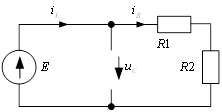
Задача 4
Дано:
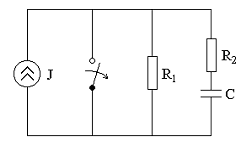
Найти:
Uc(t) – ?
Решение:
Uc(t) = Ucсв(t) + Ucпр(t)
Ucпр = J*R1/jWc/R2+1/jWc+R1 ;
Ucсв = A e pt
A = Uc(0+) - Ucпр(0+) ; Uc(0+) = 0;
A = - Ucпр(0) ;
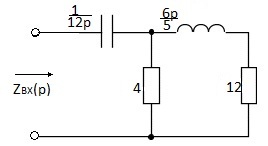
zвх= R1 + R2 + 1/PC;
P = 1/(-R1-R2)C;
P = -1/2;
Ucпр = (e 3j*1/j)/(2-j) = (e 3j*1/j)/(2+1/j) = e 3j/j(2+1/j) = e 3j/(2j+1) = e 3j/51/2* e arctg2= e (3-arctg2)j /51/2;
Ucпр (t) = 21/2*sin(t+(3-arctg2))/ 51/2;
A = - Ucпр(0) = -21/2*sin(3-arctg2)/ 51/2;
Uc(t) = -21/2*sin(3-arctg2)/ 51/2e-t/2 + 21/2*sin(t+(3-arctg2))/ 51/2 ;
Uc(t) = 0,64*sin(t-60,40)+0,63*sin 60,40* e-t/2;
Ответ: Uc(t) = 0,64*sin(t-60,40)+0,63*sin 60,40* e-t/2;
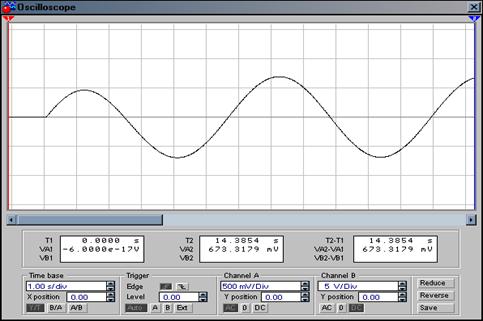
Рис. 4 - График
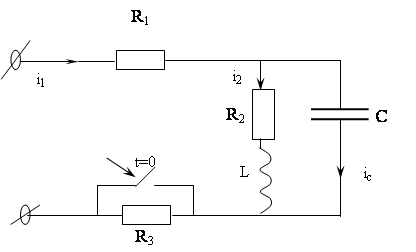
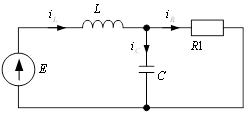
Задача 5
Дано: L = 1 Гн
C = 1 Ф
R1 = 9 Ом
R2 = 1 Ом
E = 10 B
Найти: i(t) - ?
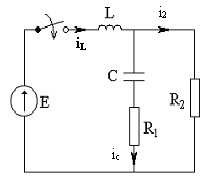
Решение:
Классический метод.
1) До коммутации:
i = i1 = i2 = 0
2) После коммутации:
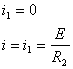
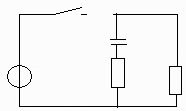
2) Переходной процесс:

![]()

- характерное уравнение с неизвестным p

Операторный метод:
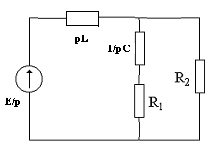
iL(0-) = 0;
UC(0-) = 0;
IL(p) = E/p/(p*L+(R2(R1+1/pC)/R1+R2+1/pC)) = E((R1+R2)pc+1)/(p((R1+R2)cLp2+pL+R1R1cp+R2))=(100p+10)/p(10p2+10p+1)
P1 = -0,113; P2 = -0,887; P0 = 0;
iL(t) = 10/1 + (-11,3+10) e –0,113t /(1+20(-0,113)+30(-0,113)2) + (-88,7+10) e –0,887t / (1+20(-0,887)+30(-0,887)2 ) = 10 + 1,48 e –0,113t – 11,47 e –0,887t;
IC(p) = IL(p) * R2/(R1+R2+1/pc) = (100p+10)p/(p(10p2+10p+1)(10p+1)) = 10/(10p2+10p+1);
iC(t) = 10 e –0,113t /(10+20(-0,113)) + 10 e –0,887t /(10+20(-0,887)) = 1,29 e –0,113t – 1,29 e –0,887t;
i(t) = iL(t) – iC(t) = 10 + 0,19 e –0,113t – 10,18 e –0,887t;
Ответ: i(t) = 10 + 0,19 e –0,113t – 10,18 e –0,887t
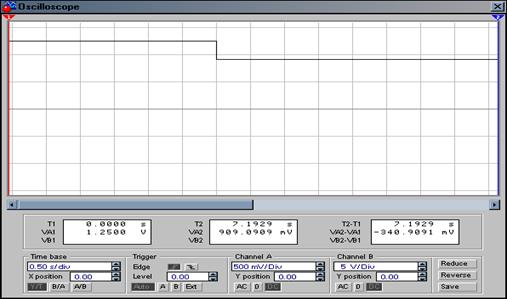
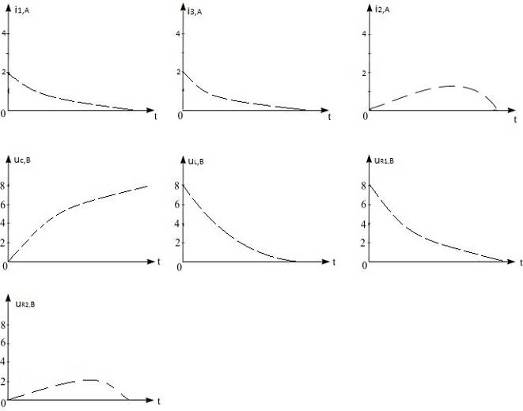
Рис. 5 – График
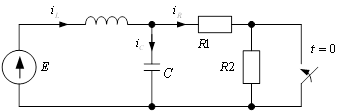
Задача 6
Дано:
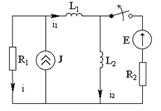
R1 = R2 = 10 Ом
L1 = L2 = 1*10-3 Гн
J = 1A
E = 5B
Найти:
i2(t) -?
Решение:
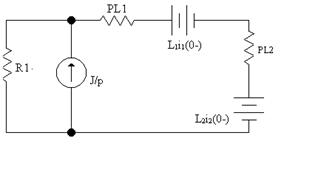
iL1(0-) = J = 1(A);
iL2(0-) = J + E/R2 = 1,5(A)
IL2(p) = J/p*(R1/R1+p(L1+L2))+((L1iL1(0-)+ L2iL2(0-))/(R1+p(L1+L2)) = (JR1+p((L1iL1(0-)+ L2iL2(0-))/(p(R1+p(L1+L2));
p1 = 0; p2 = -R1/(L1+L2)=-10/2*10-3 = -5000;
iL2(t) = 10/10 + ((10+(-5000) 10-3 * 2,5) e –5000t)/(10+4*10-3(-5000)) =
1+0,25 e –5000t;
Ответ: iL2(t) = 1+0,25 e –5000t.
Похожие работы
... пример анализа переходных процессов операторным методом, основанный на теоретических знаниях. В результате чего произведено более глубокое и эффективное изучение материала по теме: «Анализ переходных процессов в электрических цепях», а также освоение новых программ и приложений, требуемых при построении схем, графиков и расчёте формул. 1. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ 1.1 ...
... R3 R3 R1 i1 C ic U График 1: t3 1 этап курсовой работы Расчет цепи с двумя реактивными элементами в переходных процессах классическим методом 1 этап Запишем начальные ...
... i(t) либо постоянная величина i0, либо синусоидальные токи in, то для их определения применяют известные методы расчета цепей постоянного и переменного синусоидального токов. Рассчитать формы и спектры сигналов при нелинейных преобразованиях Исходные данные: U0=0,5 В, U1=1 В, Um=1,5 В, S=16 мА/В, T=11 мкс 1. Рассчитаем угол отсечки θ в радианах и градусах cos θ= ...
... . В линейной цепи – это линейные дифференциальные уравнения (ЛДУ). Существуют различные методы решения таких уравнений, и соответственно различают различные методы расчета переходных процессов. 2 Способы получение характеристического уравнения Классический метод Классический метод основан на решении ЛДУ методом вариации произвольных постоянных. Любая система ЛДУ может быть сведена к одному ...



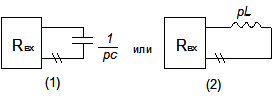
0 комментариев