Навигация
Задача 1.
Решить задачу линейного программирования симплексным методом.
Вариант 3.
Найти наибольшее значение функции f(X) = - x1 - x2 + 2x3 при ограничениях
![]() 2x1 + x2 + x3 £ 2
2x1 + x2 + x3 £ 2
x1 - x2 + x3 £ 1,
xj ³ 0, j = 1, 2, 3.
Решение.
Приведем задачу к каноническому виду, вводя дополнительные неотрицательные переменные x4,5 ³ 0.
f(X) = - x1 - x2 + 2x3 ® max
![]() 2x1 + x2 + x3 + x4 = 2
2x1 + x2 + x3 + x4 = 2
x1 - x2 + x3 + x5 = 1,
xj ³ 0, j = 1, 2, 3, 4, 5.
Каноническая задача имеет необходимое число единичных столбцов, т. е. обладает очевидным начальным опорным решением.
Очевидное начальное опорное решение (0; 0; 0; 2; 1).
Решение осуществляется симплекс-методом с естественным базисом. Расчеты оформим в симплекс-таблицах
| Номер симплекс-таблицы | Базис | Cj Ci | B | -1 | -1 | 2 | 0 | 0 | Q |
| A1 | A2 | A3 | A4 | A5 | |||||
| 0 | A4 | 0 | 2 | 2 | 1 | 1 | 1 | 0 | 2:1 = 1 |
| A5 | 0 | 1 | 1 | -1 | 1 | 0 | 1 | 1:1 = 1 | |
| j | - | 0 | 1 | 1 | -2 | 0 | 0 | ||
| 1 | A4 | 0 | 1 | 1 | 2 | 0 | 1 | -1 | 1:2 = 1/2 |
| A3 | 2 | 1 | 1 | -1 | 1 | 0 | 1 | ||
| j | - | 2 | 3 | -1 | 0 | 0 | 2 | ||
| 2 | A2 | -1 | 1/2 | 1/2 | 1 | 0 | 1/2 | -1/2 | |
| A3 | 2 | 3/2 | 3/2 | 0 | 1 | 1/2 | 1/2 | ||
| j | - | 5/2 | 7/2 | 0 | 0 | 1/2 | 3/2 |
Начальное опорное решение (0; 0; 0; 1; 1), соответствующее симплекс-таблице 0, неоптимальное, так как в D - строке есть отрицательные значения, наименьшее в столбце А3. Этот столбец будет направляющим. Минимальное положительное оценочное отношение Q в строке А5, эта строка направляющая. Направляющий элемент на пересечении направляющих строки и столбца. Столбец А5 выводим из базиса, а А3 - вводим в базис. После пересчета получаем симплекс-таблицу 1. Соответствующее опорное решение (0; 0; 1; 1; 0) не оптимально, так как в D - строке есть отрицательные значения, в столбце А2.Этот столбец будет направляющим. Минимальное положительное оценочное отношение Q в строке А4. В качестве направляющей строки возьмем А4. Направляющий элемент на пересечении направляющих строки и столбца. Столбец А4 выводим из базиса, а А2 - вводим в базис. Опорное решение, соответствующее симплекс-таблице 2 (0; 1/2; 3/2; 0; 0) - оптимально, так как в D - строке нет отрицательных значений.
Отбрасывая значения дополнительных переменных х4 и х5, получаем оптимальное решение исходной задачи:
х1 = 0, х2 = 1/2 = 0,5; х3 = 3/2 = 1,5; fmax = -1×0 - 1×0,5 + 2×1,5 = 2,5.
Задача 2.
Задание 1. Сформулировать экономико-математическую модель исходной экономической задачи.
Задание 2. Решить полученную задачу линейного программирования графическим методом.
Задание 3. Сформулировать двойственную задачу и найти ее оптимальное решение, используя теоремы двойственности.
Вариант 3.
Из 505 м2 ткани нужно сшить не более 150 женских и не более 100 детских платьев. На пошив одного женского и детского платья требуется соответственно 3 м2 и 1 м2 ткани. При реализации каждого женского платья получают 10 ден. единиц прибыли, а детского – 5 ден. единиц. Сколько нужно сшить женских и детских платьев, чтобы получить наибольшую прибыль?
Решение.
Задание 1.
Обозначим x1 и x2 количество женских и детских платьев, соответственно (план пошива). Очевидно, x1,2 ³ 0 и целые. Так как женских платьев должно быть не более 150, то x1 £ 150, аналогично, для детских платьев получаем x2 £ 100. Расход ткани на план пошива (x1, x2) составит 3x1 + x2 м2, эта величина не должна превышать запаса ткани 505 м2. Следовательно, должно выполняться неравенство 3x1 + x2 £ 505.
Прибыль от продажи платьев составит f(X) = 10x1 + 5x2 ден. единиц, и она должна быть наибольшей
Получаем экономико-математическую модель задачи:
Найти максимум функции f(X) при заданных ограничениях
f(X) = 10x1 + 5x2 ® max
3x1 + x2 £ 505
x1 £ 150
x2 £ 100
x1,2 ³ 0, целые.
Задание 2.
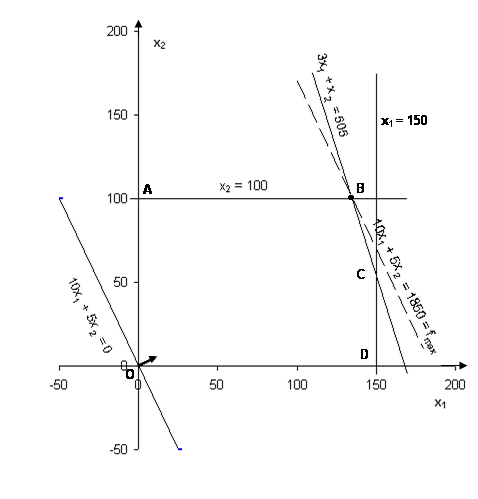
Решаем задачу без условия целочисленности решения. Построим множество допустимых решений задачи.
Прямые ограничения x1,2 ³ 0 выделяют первую четверть плоскости.
Проведем прямую 3x1 + x2 = 505 через точки (110; 175) и (175; -5). Подставим в первое неравенство координаты точки (0; 0): 3×0 +1×0 = 0 < 505, так как неравенство выполняется, то выбираем полуплоскость, содержащую эту точку.
Проведем прямую x1 = 150 и выберем левую полуплоскость.
Проведем прямую x2 = 100 и выберем нижнюю полуплоскость.
Множество допустимых решений – это многоугольник ABCDO.
Построим линию уровня целевой функции f(X) = 10x1 + 5x2 10x1 + 5x2 = 0 через точки (0; 0 ) и (-10; 20). Вектор-градиент {10; 5} задает направление, перемещаясь вдоль которого, можно увеличить значение целевой функции; перемещаясь в противоположном направлении, можно уменьшить ее значение.
Из чертежа видно, что наибольшее значение целевой функции будет на линии уровня, проходящей через точку В.
Координаты этой точки найдем из системы
![]() 3x1 + x2 = 505,
3x1 + x2 = 505,
x2 = 100.
![]() x1 = 135,
x1 = 135,
x2 = 100.
fmах = 10 ×135 + 5 ×100 = 1850 ден. единиц.
Полученное оптимальное решение оказалось целым, следовательно, это решение поставленной задачи. Получили: в оптимальном плане пошива следует сшить женских платьев 135 шт., детских – 100 шт. При этом прибыль составит 1850 ден. единиц и будет наибольшей.
Задание 3.
Двойственная задача.
Найти минимум функции g(Y) при ограничениях:
g(Y) = 505y1 + 150y2 + 100y3 ® min
3y1 + y2 ³ 10
y1 + y3 ³ 5
y1,2,3 ³ 0.
Оптимальное решение прямой задачи Х = (135; 100). Подставим его в ограничения этой задачи
3×135 + 1×100 = 505
Похожие работы
... исходной задачи (1)-(3). Для того чтобы решить задачу с ограничениями, не имеющими предпочтительного вида, вводят искусственный базис и решают расширенную М-задачу, которая имеет начальный опорный план Решение исходной задачи симплексным методом путем введения искусственных переменных называется симплексным методом с искусственным базисом. Если в результате применения симплексного метода к ...
плине: «Экономико-математические методы» на тему: «Решение задачи линейного программирования симплексным методом» Выполнила: студентка гр. КБА-081(вво) Титова Мария Дмитриевна Проверила: Старший преподаватель каф. ВМ Мягкова Светлана Васильевна Камышин - 2009 г. Задача II Для изготовления двух видов продукции P1 и P2 используют три вида сырья S1, S2, S3. На ...
... D-1 A0 = (x1, x2, ..., xi, ..., xm) отрицательная (например, xi < 0), но для всех векторов Aj выполняется соотношение Zj – Cj £ 0 (i = 1,2, ..., n). Тогда на основании теоремы двойственности Y = Сбаз D-1 - план двойственной задачи. Этот план не оптимальный, так как, с одной стороны, при выбранном базисе X содержит отрицательную компоненту и не является планом исходной задачи, а с другой ...
... при условии выпуска Х1изделий А1 и Х2 изделий А2 составляет F = 30Х₁ +49Х₂ По своему экономическому содержанию переменные Х1 и Х2 могут принимать только лишь неотрицательные значения: Х1, Х2 ≥0. Таким образом, приходим к следующей математической задаче: среди всех неотрицательных решений системы неравенств (1.1) требуется найти такое, при котором функция F = 30Х₁ +49Х&# ...

0 комментариев