Навигация
Проверим выполнение предпосылок МНК на основе анализа остаточной компоненты (см. табл. 1)
3. Проверим выполнение предпосылок МНК на основе анализа остаточной компоненты (см. табл. 1).
Независимость остатков проверяется с помощью критерия Дарбина – Уотсона по формуле ![]() , т. к.
, т. к. ![]() =0,74, d1=1,08, d2=1,36, т.е. d<d1, значит ряд остатков содержит автокорреляцию.
=0,74, d1=1,08, d2=1,36, т.е. d<d1, значит ряд остатков содержит автокорреляцию.
Для обнаружения гетероскедастичности используем тест Голдфельда – Квандта:
1) Упорядочим наблюдения по мере возрастания переменной х.
2) Разделим совокупность на 2 группы по 5 наблюдений и для каждой определим уравнение регрессии. Воспользуемся инструментом Регрессия пакета Анализ данных, полученные результаты представлены в табл. 2.
Таблица 2
| n | у1 | Предсказанное у1 | е1 | е12 | у2 | Предсказанное у2 | е2 | е22 |
| 1 | 13 | 13,81 | -0,81 | 0,66 | 22 | 22,46 | -0,46 | 0,21 |
| 2 | 15 | 16,52 | -1,52 | 2,30 | 26 | 25,73 | 0,27 | 0,07 |
| 3 | 19 | 16,52 | 2,48 | 6,16 | 26 | 27,60 | -1,60 | 2,57 |
| 4 | 20 | 21,25 | -1,25 | 1,57 | 27 | 28,07 | -1,07 | 1,15 |
| 5 | 21 | 19,90 | 1,10 | 1,21 | 30 | 27,14 | 2,86 | 8,20 |
| сумма | 11,90 | 12,20 |
3) Определим остаточную сумму квадратов для первой ![]() и второй регрессии
и второй регрессии ![]() .
.
4) Вычислим отношение 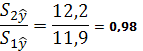 , т. к. Fнабл=0,98, Fкр(α,к1,к2)= Fкр(0,05,5,5) =5,05 (из таблицы критерия Фишера), Fнабл <Fкр, то гетероскедастичность отсутствует, предпосылка о равенстве дисперсий остаточных величии не нарушена.
, т. к. Fнабл=0,98, Fкр(α,к1,к2)= Fкр(0,05,5,5) =5,05 (из таблицы критерия Фишера), Fнабл <Fкр, то гетероскедастичность отсутствует, предпосылка о равенстве дисперсий остаточных величии не нарушена.
4. Проверим значимость параметров уравнения регрессии с помощью t‑критерия Стьюдента ![]() Расчетные значения t‑критерия Стьюдента для коэффициента уравнения регрессии а1 приведены в четвертом столбце протокола Excel, полученном при использовании инструмента Регрессия (рис. 2).
Расчетные значения t‑критерия Стьюдента для коэффициента уравнения регрессии а1 приведены в четвертом столбце протокола Excel, полученном при использовании инструмента Регрессия (рис. 2).
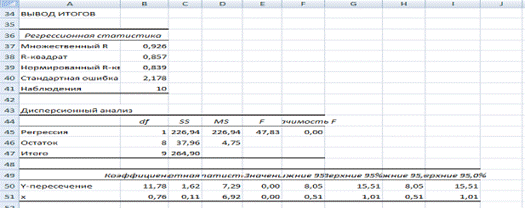
Рисунок 2
Табличное значение t‑критерия Стьюдента 2,30. tрасч=6,92, так как tрасч>tтабл, то коэффициент а1 значим.
5. Значение коэффициента детерминации (R – квадрат) можно найти в таблице Регрессионная статистика (рис. 2). Коэффициент детерминации/ Он показывает долю вариации результативного признака под воздействием изучаемых факторов. Следовательно, около 85,7% вариации зависимой переменной (объем выпуска продукции) учтено в модели и обусловлено влиянием включенного фактора (объем капиталовложений).
Значение F – критерия Фишера можно найти в таблице протокола Excel (рис. 2), Fрасч=47,83. Табличное значение F – критерия при доверительной вероятности 0,05 равно 4,46, т. к. Fрасч>Fтабл, уравнение регрессии следует признать адекватным.
Определим среднюю относительную ошибку аппроксимации? в среднем расчетные значения у для линейной модели отличаются от фактических на 1% – хорошее качество модели.
6. Осуществим прогнозирование среднего значения показателя ![]() при уровне значимости
при уровне значимости ![]() , если прогнозное значения фактора Х составит 80% от его максимального значения.
, если прогнозное значения фактора Х составит 80% от его максимального значения.
Модель зависимости объема выпуска продукции от величины капиталовложений у=11,78+0,76х. Для того чтобы определить среднее значение фактора У при 80% максимального значения фактора Х, необходимо подставить Хпрогн=Хmax*0,8=22*0,8=17,6 в полученную модель: Упрогн=11,78+0,76*17,6=25,17
Для построения интервального прогноза рассчитаем доверительный интервал. Критерий Стьюдента (при v=n -2=10–2=8) равен 1,8595. Ширину доверительного интервала вычислим по формуле:
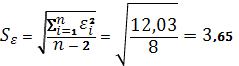
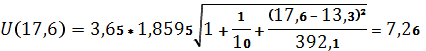 ,
,
таким образом, прогнозное значение будет находиться между:
Yпрогн(80 % max)+= 25,17+7,26=32,43 – верхняя граница прогноза,
Yпрогн(80 % max) – =25,17–7,26=17,91 – нижняя граница прогноза.
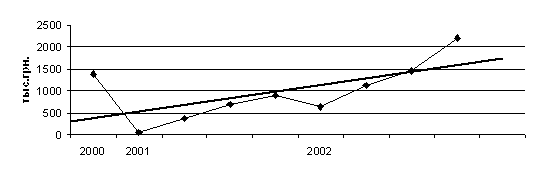
7. Графическое представление (рис. 3) модели парной регрессии зависимости объема выпуска продукции от объема капиталовложений: фактические и модельные значения ![]() точки прогноза.
точки прогноза.
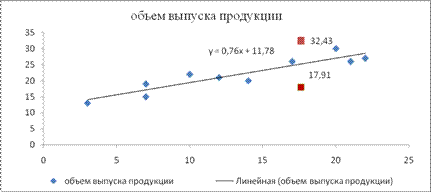
Рисунок 3
8. Уравнение гиперболической функции: y=a+b/x. Произведем линеаризацию путем замены Х=1/х. В результате получим линейное уравнение y=a+bХ. Рассчитаем его параметры по данным таблицы 3
Таблица 3
| n | х | у | Х | уХ | Х2 | y-ycp | (у-уср)2 | Упр | ε | ε2 | /ε/у/*100% |
| 1 | 17 | 26 | 0,05882 | 1,52941 | 0,0035 | 4,1 | 16,81 | 24,3846 | 1,62 | 2,61 | 6,213 |
| 2 | 22 | 27 | 0,04545 | 1,22727 | 0,0021 | 5,1 | 26,01 | 25,066 | 1,93 | 3,74 | 7,163 |
| 3 | 10 | 22 | 0,10000 | 2,20000 | 0,0100 | 0,1 | 0,01 | 22,2859 | -0,29 | 0,08 | 1,299 |
| 4 | 7 | 19 | 0,14286 | 2,71429 | 0,0204 | -2,9 | 8,41 | 20,1015 | -1,10 | 1,21 | 5,797 |
| 5 | 12 | 21 | 0,08333 | 1,75000 | 0,0069 | -0,9 | 0,81 | 23,1354 | -2,14 | 4,56 | 10,168 |
| 6 | 21 | 26 | 0,04762 | 1,23810 | 0,0023 | 4,1 | 16,81 | 24,9557 | 1,04 | 1,09 | 4,016 |
| 7 | 14 | 20 | 0,07143 | 1,42857 | 0,0051 | -1,9 | 3,61 | 23,7422 | -3,74 | 14,00 | 18,711 |
| 8 | 7 | 15 | 0,14286 | 2,14286 | 0,0204 | -6,9 | 47,61 | 20,1015 | -5,10 | 26,02 | 34,010 |
| 9 | 20 | 30 | 0,05000 | 1,50000 | 0,0025 | 8,1 | 65,61 | 24,8344 | 5,17 | 26,68 | 17,219 |
| 10 | 3 | 13 | 0,33333 | 4,33333 | 0,1111 | -8,9 | 79,21 | 10,3929 | 2,61 | 6,80 | 20,054 |
| сумма | 219 | 20,0638 | 0,1843 | 265 | 219 | 0,00 | 86,80 | 124,65 | |||
| ср. знач. | 13,3 | 21,9 | 0,10757 | 2,00638 | 0,0184 | 12,465 |
![]() ,
,
получим следующее уравнение гиперболической модели: ỹ =27,38–50,97/х.
Уравнение степенной модели имеет вид: у=а*хb. Для линеаризации переменных произведем логарифмирование обеих частей уравнения: lgy=lga+blgx. Обозначим Y=lgy', X=lgx, A=lga. Тогда уравнение примет вид Y=A+bX – линейное уравнение регрессии. Рассчитаем его параметры, используя данные табл. 4:
Таблица 4
| n | у | Y=lg(y) | х | X=lg(x) | YX | X2 | yпр | ε | ε2 | |ε/y|*100% |
| 1 | 26 | 1,415 | 17 | 1,230 | 1,741 | 1,514 | 24,823 | 1,177 | 1,385 | 0,045 |
| 2 | 27 | 1,431 | 22 | 1,342 | 1,921 | 1,802 | 27,476 | -0,476 | 0,226 | 0,018 |
| 3 | 22 | 1,342 | 10 | 1,000 | 1,342 | 1,000 | 20,142 | 1,858 | 3,452 | 0,084 |
| 4 | 19 | 1,279 | 7 | 0,845 | 1,081 | 0,714 | 17,503 | 1,497 | 2,242 | 0,079 |
| 5 | 21 | 1,322 | 12 | 1,079 | 1,427 | 1,165 | 21,641 | -0,641 | 0,411 | 0,031 |
| 6 | 26 | 1,415 | 21 | 1,322 | 1,871 | 1,748 | 26,977 | -0,977 | 0,955 | 0,038 |
| 7 | 20 | 1,301 | 14 | 1,146 | 1,491 | 1,314 | 22,996 | -2,996 | 8,975 | 0,150 |
| 8 | 15 | 1,176 | 7 | 0,845 | 0,994 | 0,714 | 17,503 | -2,503 | 6,263 | 0,167 |
| 9 | 30 | 1,477 | 20 | 1,301 | 1,922 | 1,693 | 26,464 | 3,536 | 12,505 | 0,118 |
| 10 | 13 | 1,114 | 3 | 0,477 | 0,531 | 0,228 | 12,537 | 0,463 | 0,214 | 0,036 |
| сумма | 219 | 13,273 | 10,589 | 14,322 | 11,891 | 0,939 | 36,630 | 0,764 | ||
| ср. знач. | 1,327 | 1,059 | 1,432 | 1,189 | 0,076 |
Уравнение регрессии будет иметь вид: У=0,9103+0,3938*Х. Перейдем к исходным переменным х и у, выполнив потенцирование данного уравнения: ỹ=100,9103*х0,3938.
Получим уравнение степенной модели регрессии: ỹ=8,1339*х0,3938.
Уравнение показательной кривой: ỹ=а*bx. Осуществим логарифмирование обеих частей уравнения: lgy=lga+x*lgb. Обозначим Y=lgy', В=lgb, A=lga. Получим линейное уравнение регрессии: Y=A+Вх. Рассчитаем его параметры, используя данные табл. 5
Таблица 5
| n | у | Y=lg(y) | х | Ух | х2 | У-Уср | (У-Уср)2 | х-хср | (х-хср)2 | Упр | ε | ε2 | |ε/y|*100% |
| 1 | 26 | 1,415 | 17 | 24,0545 | 289 | 0,088 | 0,008 | 3,7 | 13,69 | 24,365 | 1,635 | 2,673 | 26 |
| 2 | 27 | 1,431 | 22 | 31,49 | 484 | 0,104 | 0,011 | 8,7 | 75,69 | 29,318 | -2,318 | 5,375 | 27 |
| 3 | 22 | 1,342 | 10 | 13,4242 | 100 | 0,015 | 0,000 | -3,3 | 10,89 | 18,804 | 3,196 | 10,21 | 22 |
| 4 | 19 | 1,279 | 7 | 8,95128 | 49 | -0,049 | 0,002 | -6,3 | 39,69 | 16,827 | 2,173 | 4,720 | 19 |
| 5 | 21 | 1,322 | 12 | 15,8666 | 144 | -0,005 | 0,000 | -1,3 | 1,69 | 20,248 | 0,752 | 0,565 | 21 |
| 6 | 26 | 1,415 | 21 | 29,7144 | 441 | 0,088 | 0,008 | 7,7 | 59,29 | 28,253 | -2,253 | 5,076 | 26 |
| 7 | 20 | 1,301 | 14 | 18,2144 | 196 | -0,026 | 0,001 | 0,7 | 0,49 | 21,804 | -1,804 | 3,255 | 20 |
| 8 | 15 | 1,176 | 7 | 8,23264 | 49 | -0,151 | 0,023 | -6,3 | 39,69 | 16,827 | -1,827 | 3,339 | 15 |
| 9 | 30 | 1,477 | 20 | 29,5424 | 400 | 0,150 | 0,022 | 6,7 | 44,89 | 27,226 | 2,774 | 7,693 | 30 |
| 10 | 13 | 1,114 | 3 | 3,34183 | 9 | -0,213 | 0,046 | -10,3 | 106,09 | 14,512 | -1,512 | 2,285 | 13 |
| сумма | 219 | 13,273 | 133 | 182,832 | 2161 | 0,120 | 392,1 | 0,814 | 45,199 | 219 | |||
| ср. зн | 1,327 | 13,3 | 18,2832 | 216,1 |
Уравнение имеет вид: У=1,11+0,0161х. Перейдем к исходным переменным х и у, выполнив потенцирование уравнения:
ỹ =101,11(10 0,0161)х, ỹ =12,99*1,038х – уравнение показательной кривой.
Графики построенных уравнений регрессии приведены на рис. 4.
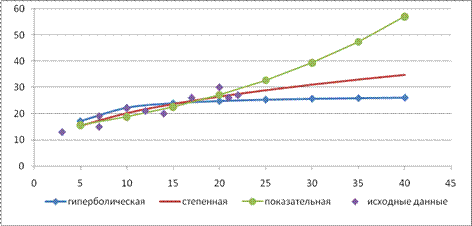
Рисунок 4
9. Коэффициент детерминации: 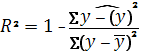
Для сравнения и выбора лучшей модели строим сводную таблицу результатов (табл. 6).
Таблица 6
| Параметры Модель | коэффициент детерминации | средняя относительная ошибка аппроксимации | коэффициент эластичности |
| гиперболическая | 0,672 | 7,257 | -0,250 |
| степенная | 0,862 | 0,034 | 0,239 |
| показательная | 0,829 | 3,82 | 0,010 |
Вывод: на основании полученных данных лучшей является степенная модель регрессии, т. к. она имеет наибольший коэффициент детерминации R2=0,862, т.е. вариация факторного признака У (объем выпуска продукции) на 86,2% объясняется вариацией фактора Х (объемом капиталовложений), и наименьшую относительную ошибку (в среднем расчетные значения для степенной модели отличаются от фактических данных на 0,034%). Также степенная модель имеет наибольший коэффициент эластичности, т.е. при изменении фактора на 1% зависимая переменная изменится на 0,24%, таким образом степенную модель можно взять в качестве лучшей для построения прогноза.
Задача 2а и 2б
Имеются два варианта структурной формы модели, заданные в виде матриц коэффициентов модели. Необходимо для каждой матрицы записать системы одновременных уравнений и проверить их на идентифицируемость.
Задача 2а
Решение.
Запишем систему одновременных уравнений:
у1= b12 у2+ b13 у3+ a12 х2+ a13 х3
у2= b23 у3+ a21 х1+ a22 х2+ a24 x4
у3 = b32 у2+ a31 х1+ a32х2+a33х3
Проверим каждое уравнение на выполнение необходимого и достаточного условия идентификации.
1) В первом уравнении три эндогенные переменные у1, у2, у3 (Н=3). В нем отсутствуют экзогенные переменные х1, х4 (D=2). Необходимое условие идентификации D+1=H, 2+1=3 выполнено.
Для проверки на достаточное условие составим матрицу из коэффициентов при переменных х1 и х4 (табл. 7)
Таблица 7
| Уравнения, из которых взяты коэффициенты при переменных | Переменные | |
| х1 | х4 | |
| 2 | a21 | a24 |
| 3 | a31 | 0 |
Определитель матрицы не равен нулю, а ранг матрицы равен 2. Значит, достаточное условие выполнено, первое уравнение идентифицируемо.
2) Во втором уравнении две эндогенные переменные у2, у3 (Н=2). В нем отсутствует экзогенная переменная х3 (D=1). Необходимое условие идентификации D+1=H, 1+1=2 выполнено.
Для проверки на достаточное условие составим матрицу из коэффициентов при переменных у1 и х3 (табл. 8)
Таблица 8
| Уравнения, из которых взяты коэффициенты при переменных | Переменные | |
| у1 | х3 | |
| 1 | -1 | a13 |
| 3 | 0 | a33 |
Определитель матрицы не равен нулю, а ранг матрицы равен 2. Значит, достаточное условие выполнено, второе уравнение идентифицируемо.
3) В третьем уравнении две эндогенные переменные у2, у3 (Н=2). В нем отсутствует экзогенная переменная х4 (D=1). Необходимое условие идентификации D+1=H, 1+1=2 выполнено.
Для проверки на достаточное условие составим матрицу из коэффициентов при переменных у1 и х4 (табл. 9)
Таблица 9
| Уравнения, из которых взяты коэффициенты при переменных | Переменные | |
| у1 | х4 | |
| 1 | -1 | 0 |
| 2 | 0 | a24 |
Определитель матрицы не равен нулю, а ранг матрицы равен 2. Значит, достаточное условие выполнено, третье уравнение идентифицируемо.
Вывод: все уравнения системы идентифицируемы, систему можно решать.
Задача 2б
Решение
Запишем систему уравнений:
у1=b13у3+a11 х1+a13 х3+a14 х4
у2= b21 у1+b23 у3+a22 х2+a24 х4
у3=b31 у1+a31 х1+a33 х3+a34 х4
Проверим каждое уравнение на выполнение необходимого и достаточного условия идентификации.
1) В первом уравнении две эндогенные переменные у1, у3 (Н=2). В нем отсутствует экзогенная переменная х2 (D=1). Необходимое условие идентификации D+1=H, 1+1=2 выполнено.
Для проверки на достаточное условие составим матрицу из коэффициентов при переменных у2 и х2 (табл. 10)
Таблица 10
| Уравнения, из которых взяты коэффициенты при переменных | Переменные | |
| у2 | х2 | |
| 2 | -1 | a22 |
| 3 | -1 | 0 |
Определитель матрицы не равен нулю, а ранг матрицы равен 2. Значит, достаточное условие выполнено, первое уравнение идентифицируемо.
2) Во втором уравнении три эндогенные переменные у1, у2, у3 (Н=3). В нем отсутствуют экзогенные переменные х1, х3 (D=2). Необходимое условие идентификации D+1=H, 2+1=3 выполнено.
Для проверки на достаточное условие составим матрицу из коэффициентов при переменных х1 и х3 (табл. 11)
Таблица 11
| Уравнения, из которых взяты коэффициенты при переменных | Переменные | |
| х1 | х3 | |
| 1 | a11 | а13 |
| 3 | a31 | a33 |
Определитель матрицы не равен нулю, а ранг матрицы равен 2. Значит, достаточное условие выполнено, первое уравнение идентифицируемо.
3) В третьем уравнении две эндогенные переменные у1, у3 (Н=2). В нем отсутствует экзогенная переменная х2 (D=2). Необходимое условие идентификации D+1=H, 1+1=2 выполнено.
Для проверки на достаточное условие составим матрицу из коэффициентов при переменных у2 и х2 (табл. 12)
Таблица 12
| Уравнения, из которых взяты коэффициенты при переменных | Переменные | |
| у2 | х2 | |
| 1 | 0 | 0 |
| 2 | -1 | a22 |
Определитель матрицы равен нулю (первая строка состоит из нулей). Значит, достаточное условие не выполнено, и третье уравнение нельзя считать идентифицируемым.
Вывод: не все уравнения системы идентифицируемы, систему решать нельзя.
Задача 2в
По данным таблицы для своего варианта, используя косвенный метод наименьших квадратов (КМНК), построить структурную форму модели вида:
y1= a01 + b12 y2 + a11 x1 + e1
y2= a02 + b21 y1 + a22 x2 + e2
| Вар. | n | y1 | y2 | x1 | x2 |
| 8 | 1 | 61,3 | 31,3 | 9 | 7 |
| 2 | 88,2 | 52,2 | 9 | 20 | |
| 3 | 38,0 | 14,1 | 4 | 2 | |
| 4 | 48,4 | 21,7 | 2 | 9 | |
| 5 | 57,0 | 27,6 | 7 | 7 | |
| 6 | 59,7 | 30,3 | 3 | 13 |
Решение
Для построения модели мы располагаем информацией, представленной в табл. 13.
Таблица 13. Фактические данные для построения модели
| n | y1 | y2 | x1 | x2 |
| 1 | 61,3 | 31,3 | 9 | 7 |
| 2 | 88,2 | 52,2 | 9 | 20 |
| 3 | 38 | 14,1 | 4 | 2 |
| 4 | 48,4 | 21,7 | 2 | 9 |
| 5 | 57 | 27,6 | 7 | 7 |
| 6 | 59,7 | 30,3 | 3 | 13 |
| Сумма | 352,60 | 177,20 | 34,00 | 58,00 |
| Среднее значение | 58,77 | 29,53 | 5,67 | 9,67 |
Структурная форма модели преобразуется в приведенную форму:
у1=d11x1+d12x2+u1
y2=d21x1+d22x2+u2, где u1 и u2 – случайные ошибки.
Для каждого уравнения приведенной формы при расчете коэффициентов d можно применить МНК. Для упрощения расчетов можно работать с отклонениями от средних уровней у=у-уср и х=х-хср. Преобразованные таким образом данные табл. 13 сведены в табл. 14. Здесь же показаны промежуточные рассчеты, необходимые для определения коэффициентов d.
Таблица 14
| n | у1 | у2 | х1 | х2 | у1*х1 | х12 | х1*х2 | у1*х2 | у2*х1 | у2*х2 | х22 |
| 1 | 2,53 | 1,77 | 3,33 | -2,67 | 8,444 | 11,111 | -8,889 | -6,756 | 5,889 | -4,711 | 7,111 |
| 2 | 29,43 | 22,67 | 3,33 | 10,33 | 98,111 | 11,111 | 34,444 | 304,144 | 75,556 | 234,222 | 106,778 |
| 3 | -20,77 | -15,43 | -1,67 | -7,67 | 34,611 | 2,778 | 12,778 | 159,211 | 25,722 | 118,322 | 58,778 |
| 4 | -10,37 | -7,83 | -3,67 | -0,67 | 38,011 | 13,444 | 2,444 | 6,911 | 28,722 | 5,222 | 0,444 |
| 5 | -1,77 | -1,93 | 1,33 | -2,67 | -2,356 | 1,778 | -3,556 | 4,711 | -2,578 | 5,156 | 7,111 |
| 6 | 0,93 | 0,77 | -2,67 | 3,33 | -2,489 | 7,111 | -8,889 | 3,111 | -2,044 | 2,556 | 11,111 |
| Σ | 0,00 | 0,00 | 0,00 | 0,00 | 174,333 | 47,333 | 28,333 | 471,333 | 131,267 | 360,767 | 191,333 |
Для нахождения коэффициентов первого приведенного уравнения можно использовать систему нормальных уравнений:
Σу1х1=d11Σx12+d12Σx1x2;
Σy1x2=d11Σx1x2+d12Σx22.
Подставляя рассчитанные в табл. 14 значения сумм, получим:
174,333= 47,333d11+28,333d12
471,333=28,333d11+191,333d12.
Решение этих уравнений дает значения d11=2,423, d12=2,105. Первое уравнение приведенной формы примет вид: у1=2,423х1+2,105х2+u1.
Для нахождения коэффициентов второго приведенного уравнения можно использовать систему нормальных уравнений:
Σу2х1=d21Σx12+d22Σx1x2
Σy2x2=d21Σx1x2+d22Σx22
Подставляя рассчитанные в табл. 14 значения сумм, получим:
131,267=47,333d21+28,333d22
360,767=28,333d21+191,333d22.
Решение этих уравнений дает значения d21=1,805, d22=1,618. Второе уравнение приведенной формы примет вид: у2=1,805х1+1,618х2+u2
Для перехода от приведенной формы к структурной форме модели найдем х2из второго уравнения приведенной модели:
х2=(у2-1,805х1)/1,618.
Подставив это выражение в первое уравнение приведенной модели, найдем структурное уравнение:
у1=2,423х1+2,105 (у2-1,805х1)/1,618=2,423х1+1,3у2-1,115х1=1,3у2+1,308х1
Таким образом, b12=1,3 а11=1,308.
Найдем х1 из первого уравнения у1=2,423х1+2,105х2 приведенной формы:
х1=(у1-2,105х2)/2,423
Подставив это выражение во второе уравнение приведенной модели, найдем структурное уравнение:
у2=1,805 (у1-2,105х2)/2,423+1,618х2=0,745 у1-0,868х2 +1,618х2=0,745у1+0,75х2
Таким образом, b21= 0,745 а22=0,75
Свободные члены структурной формы находим из уравнений:
А01=у1,ср-b12у2,ср-а11х1,ср=58,77 – 1,3*29,53–1,308*5,67=14,04
А02=у2,ср-b21у1,ср-а22х2,ср=29,53–0,745*58,77–0,75*9,67=-5,83
Окончательный вид структурной модели:
y1= a01 + b12 y2 + a11 x1 + e1=14,04+1,3у2+1,308х1+ e1;
y2= a02 + b21 y1 + a22 x2 + e2=-5,83+0,745у1+0,75х2+ e2.
Похожие работы
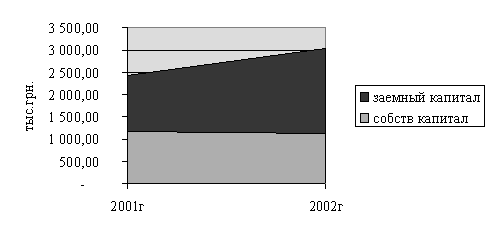
... от темпов роста совокупных активов, что свидетельствует о торможении развития предприятия и ухудшении его финансового состояния в этот период. 5. МЕТОДИЧЕСКИЕ РЕКОММЕНДАЦИИ ПО ПРИНЯТИЮ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ НА ОСНОВАНИИ ФИНАНСОВОГО АНАЛИЗА 5.1 Анализ кредитоспособности ОАО «ММК им. Ильича» Предприятия часто прибегают к услугам коммерческих банков, чтобы покрыть свою дополнительную ...
объема экспериментальных исследований. Применение современной вычислительной техники позволяет в ряде случаев упростить процедуру определения релаксационных констант. Особенно этот метод эффективен, с нашей точки зрения, при изучении релаксационных процессов в модифицированных полимерных материалах, когда известны релаксационные константы полимера-связующего. Суть подхода в определении U, Tm и B ...
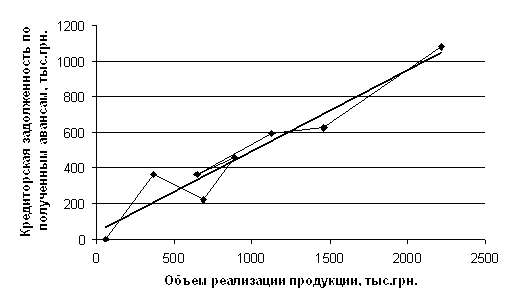
... можно прогнозировать динамику уровня кредиторской задолженности предприятия по полученным авансам при планировании изменения объемов реализации продукции на ОАО СЗКО «Молот». 3.5 Автоматизация анализа текущих обязательств Экономический анализ сопровождается выполнением большого объема разнообразных вычислений: абсолютных и относительных отклонений; средних величин; дисперсии; процентных ...
... по данным производственных измерений. Таким образом, найденное уравнение регрессии описывает совместное влияние x 1 и x2 на функцию у. Коэффициенты a, b 1 и b 2 при этом имеют математический смысл. Коэффициент а равен функции у при нулевых значениях аргументов x1 и x 2. В геометрической интерпретации коэффициент а соответствует ординате точки пересечения плоскости регрессии Р с осью ...
0 комментариев