Статистика

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

ХАРЬКОВСКИЙ НАЦИОНАЛЬНЫЙ

АВТОМОБИЛЬНО-ДОРОЖНЫЙ УНИВЕРСИТЕТ

Кафедра экономики и организации производства

Контрольная работа

по дисциплине «Статистика»

Выполнила:

Студентка группы

ХАРЬКОВ

2008

Задача № 1

На СТО легковых автомобилей изучается закономерность поступления в кассу выручки (в грн.) от ремонта и обслуживания одного автомобиля (Хі). В результате предварительной обработки данных за отчетный месяц получен интервальный вариационный ряд значений изучаемого признака. Требуется рассчитать показатели показательной статистики, построить графические изображения вариационного ряда и с их использованием дать изучаемому явлению общую характеристику

Ответы на вопросы

Изучаемый статистический показатель – поступление в кассу выручки

Единицей измерения данного показателя является сумма выручки

Показатель относится к дискретной случайной величине, т.к. варианты представлены отдельными значениями признака и частоты относятся к отдельным значениями признака.

Частота наблюдения изучаемого показателя является количество машин.

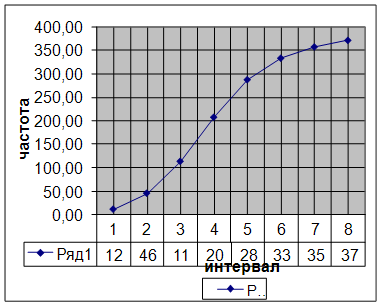
интервал j=1……K	границы интервала		xj	fј	Wj %	накопленная		xj*fј	(xj -x )*fј	(xj -x )²*fј	(xj -x )4*fј
	нижняя хј	верхняя xј+1				частота Vfj	частность Vwj
j=1	22,00	26,00	24	12	3,23	12	3,23	288,00	288,00	2147,12	384176,66
j=2	26,00	30,00	28	34	9,14	46	12,37	952,00	952,00	2989,14	262792,56
j=3	30,00	34,00	32	68	18,28	114	30,65	2176,00	2176,00	1965,55	56814,23
j=4	34,00	38,00	36	94	25,27	208	55,91	3384,00	3384,00	178,07	337,32
j=5	38,00	42,00	40	80	21,51	288	77,42	3200,00	3200,00	550,69	3790,68
j=6	42,00	46,00	44	46	12,37	334	89,78	2024,00	2024,00	2018,15	88541,91
j=7	46,00	50,00	48	24	6,45	358	96,24	1152,00	1152,00	2708,69	305708,30
j=8	50,00	54,00	52	14	3,76	372	100,0	728,00	728,00	2993,92	640253,37
ИТОГО				372	100,0			13904,00	13904,00	15551,31	1742415,02

Расчет средней арифметической, взвешенной по частоте наблюдений

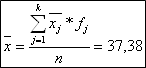
Расчет моды

Расчет медианы

Расчет показателей вариации

а) Вариационный размах

в) Дисперсия:

количественного признака

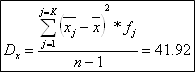
г) Среднее квадратическое отклонение:

количественного признака

д) Коэффициент вариации

е) Показатель формообразования:

коэффициент асимметрии

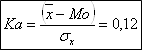
Ka>0, имеет место правостороннее- эксцесс

Е<3, то распределение низко вершинное.

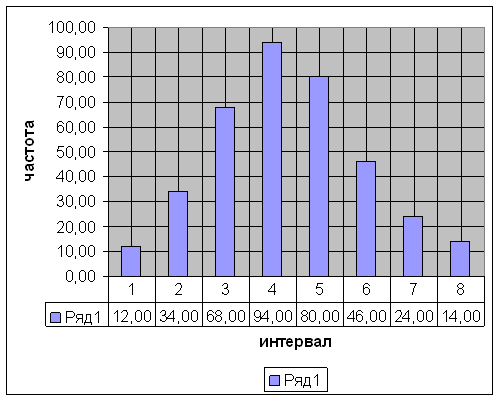
Общая характеристика изучаемого явления.

В задаче изучается поступление в кассу выручки за отчетный месяц. Объём наблюдений 372 машины и является выборочной совокупностью.

Наиболее вероятным считается значение показателя 37,38 маш. – равное среднему арифметическому значению.

Чаще всего может наблюдаться значение показателя 36,60, соответствующее моде.

Относите6льно значения показателя

Значения изучаемого признака сильно варьируют вокруг его среднего значения (Ку=17,32).

Задача № 2

Используя исходные данные и результаты решение задачи №1 рассчитать объем собственно-случайной выборки, гарантирующей оценку генеральной средней с ошибкой не более Пd процентов, при условии, что за год на СТО ремонтируют и обслуживают примерно N автомобилей (объем генеральной совокупности); построить доверительный интервал для оценки генеральной средней, соответствующий уровню доверительной вероятности Р. Значение параметров Пd, N, P принять согласно варианту. Уровень доверительной вероятности 0,99 соответствует коэффициент доверия tv=2,6

Пd % =	1,00
N =	6500,00
P =	0,99
tv =	2,60

В условии задана желаемая относительная ошибка оценки параметра в процентах Пd, то необходимо рассчитать допустимую предельную абсолютная величина ошибки оценки генеральной средней ∆х.

Доверительные интервалы, заключающие генеральную среднюю с заданной вероятностью, строятся в соответствии со следующими условиями:

37,01-0,37 ≤ Xr ≤ 37,01 + 0,37

36,64 ≤ Xr ≤ 37,38

Расчет минимального объема выборки производится по формуле

Рассчитать предельную ошибку оценки генеральной средней по выборке, используя формулу бесповторной выборки.

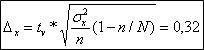
Выводы: Генеральная средняя в случае оценки ее по данным выборки (задачи №1) может находится в интервале от 36,64 до 37,38.

Задача № 3

Изучается зависимость годового дохода предприятий от реализации продукции от суммарных годовых затрат предприятия на ее рекламу. Получены данные по восьми предприятиям о годовых затратах на рекламу (Xi) и валовом доходе от продажи рекламируемой продукции (Y). Требуется провести корреляционно-регрессионный анализ этой зависимости и определить с использованием модели регрессии значение валового дохода предприятия, которое планирует затратить на рекламу Хi тыс.гривень.

Расчет сумм для оценки коэффициента корреляции и параметров модели регрессии вида :

Номер наблюдения j						Оценка значимости модели
1	10,0	240,4	100,00	57792,16	2404,000	279,999	7052,012	1568,060
2	12,9	360,2	166,41	129744,04	4646,580	318,426	2074,734	1745,088
3	15,8	360,0	249,64	129600,00	5688,000	356,853	50,726	9,905
4	16,2	380,2	262,44	144552,04	6159,240	362,153	3,320	325,693
5	17,4	386,4	302,76	149304,96	6723,360	378,054	198,214	69,658
6	18,2	384,2	331,24	147609,64	6992,440	388,654	609,073	19,842
7	19,8	398,2	392,04	158563,24	7884,360	409,856	2105,022	135,851
8	20,4	402,2	416,16	161764,84	8204,880	417,806	2897,770	243,545
Итого:	130,7	2911,8	2220,69	1078930,92	48702,860	2911,80	14990,872	4117,643

Ответы на вопросы

В задаче зависимой переменной являются валовые доходе от продажи рекламируемой продукции (Yі), а независимой - годовые затраты на рекламу (Хі).

С увеличением независимой переменной значения зависимой переменной увеличивается.

Корреляционной связью называется разновидность стохастической связи, при которой каждому значению одной величины соответствует математическое ожидание другой величины. Корреляция возникает тогда, когда зависимость одного из признаков от другого осложняется наличием ряда случайных факторов. Силу корреляционной связи оценивают при помощи коэффициента корреляции.

Регрессионный анализ – это выбор формы связи (уровня регрессии), оценка параметров регрессии и статистической значимости результатов.

Для расчета параметров модели регрессии применяется метод наименьших квадратов, в основу которого положено требование: сумма квадратов отклонений эмпирических данных от теоретических должна быть минимальной.

Статистическая значимость модели регрессии или ее параметров – это ситуация, когда проверяется гипотеза о равенстве их нулю с вероятностью ошибки а (а – уровень зависимости критерия проверки гипотезы) и она не подтвердилась.

Для проверки гипотезы о значимости модели регрессии применяется F-критерий Фишера, а для проверки статистической зависимости параметров модели – t – критерий Стьюдента.

 Расчет параметров модели регрессии вида :

 

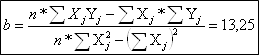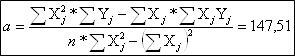Используя полученные суммы, рассчитаем значение коэффициента парной корреляции по формуле:

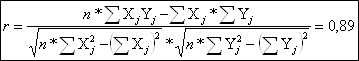
Абсолютная величина этого коэффициента изменяется в пределах от нуля до единицы. В нашем случае значение близко к единице, значить связь высокая.

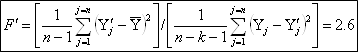
Расчетное значение F-критерия показало, что 2,6 раза ошибка предсказаний результативного показателя по регрессионной модели меньше ошибки, получаемой в случае использования для этой цели среднего значения показателя.

Выводы: В результате анализа корреляционной связи была установленная прямая функциональная зависимость между годовым доходом предприятия от реализации продукции и суммарных годовых затрат предприятия на рекламу. Полученная модель регрессии пригодна для практического применения.

Задача № 4

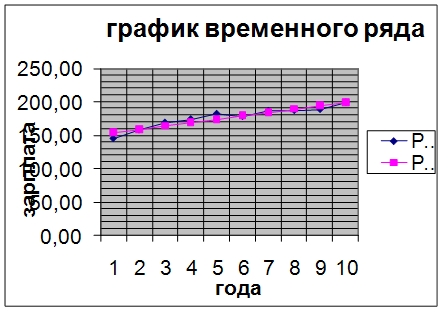
В предприятии осуществляется разработка плана деятельности на следующий год. Предложены данные за последние 10 лет о среднемесячной заработной плате работников предприятия (Yj). Требуется проанализировать тенденцию изменения изучаемого показателя и определить его прогнозное значение на следующий год (t=11)

Ответы на вопросы:

Временным рядом называется ряд, расположенный в хронологической последовательности числовых значений статистического показателя, характеризующих изменение общественных явлений во времени.

Временной ряд отличается от вариационного ряда привязкой к определенному периоду времени.

Ряд динамики изучаемого показателя является моментным, потому что его значения даны на определенный момент времени, стационарным и монотонно возрастающим.

Изучение ряда динами позволяет выявить и измерить закономерности развития социально-экономических явлений во времени.

Каждое наблюдение ряда динамики называется уровнем ряда.

Уровни в рядах динамики могут быть представлены абсолютными, относительными и средними величинами.

Расчет сумм для оценки уровня тренда вида

Номер периода t
1	145,00	1,00	145,00	154,22	9,22
2	158,00	4,00	316,00	159,22	1,22
3	169,00	9,00	507,00	164,22	4,78
4	174,00	16,00	696,00	169,23	4,77
5	182,00	25,00	910,00	174,23	7,77
6	178,00	36,00	1068,00	179,23	1,23
7	186,50	49,00	1305,50	184,23	2,27
8	187,00	64,00	1496,00	189,24	2,24
9	188,60	81,00	1697,40	194,24	5,64
10	199,20	100,00	1992,00	199,24	0,04
11	204,62			204,21
55	1767,30	385,00	10132,90	1767,30	39,18

Рассчитаем параметры a и b по формулам:

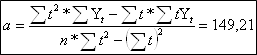Прогноз по уровню тренда:

Прогноз с использованием среднего темпа роста значений показателя равно 204,62 грн.

Оценка качества предсказания значений показателя по уравнению тренда.

В полученную числовую модель подставляем значения t=1,2,……10 и вычисляем соответствующие прогнозные значения Yt`, сравнить их с фактическими значениями Yt.

По полученным данным строим линию тренда временного ряда. Линия полигона и линия тренда очень близки, это означает, что тренд хорошо описывает характер изменения показателя во времени.

Рассчитываем среднюю описательную ошибку предсказания по формуле:

 

Можно считать, что прогнозы будут сбываться с вероятностью 97,69 % (100-2,31)

Выводы: Определив прогнозное значение заработной платы работникам предприятия можно сказать, что прогноз по уравнению тренда более точно описывает закономерность, так как рассматривается весь анализируемый период и учитывает не только общую тенденцию развития показателя во времени, но и случайные колебания.