Российский государственный гидрометеорологический университет
Экономический и социально-гуманитарный факультет
Кафедра Экономики и менеджментаКурсовая работа
по дисциплине «Информатика»
Статистические модели макроэкономики
Санкт-Петербург
2008г.
1. Постановка задачи.
Даны: вектор непроизводственного потребления ![]() , матрицы межотраслевого баланса
, матрицы межотраслевого баланса ![]() и
и ![]() .
.
1. Рассчитать матрицу В.
2. Найти вектор валового выпуска х, обеспечивающий данный вектор потребления.
3. Рассчитать произведение вектора на матрицу А×х.
4. Рассчитать вектор ![]() .
.
Все расчеты произвести с использованием программы, написанной на алгоритмическом языке ПАСКАЛЬ.
| № варианта | Вектор потребления, | Матрица межотраслевого баланса | Матрица межотраслевого баланса |
| 1 | 1/3 | 1/3 1/6 ½ ¼ | ½ ¼ ¼ 1/4 |
 | |||||||||
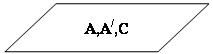 | |||||||||
![]()
|
![]()
![]()
![]()
|
|
|
|
|
|
|
|
|
|
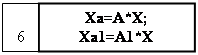 | ||||||||||||
 | ||||||||||||
 | ||||||||||||
 |  | |||||||||||
![]()
![]()

program KURSOVOJ_PROJECT;
uses crt;
type int=0..10;
vec=array [0..10] of real;
matr=array [0..10,0..10] of real;
var x,x_1,ax,ax_1,c:vec;
e,a,a_1,b,b_1,br,br_1: matr;
m,n:int;
name:char;
procedure readvec (var x:vec; name:char; n:int);
var i:int;
begin
writeln(' Ввести вектор ',name,' размера n=', n); for i:=0 to n-1 do
begin
write (' ',name,'[',i:2,']='); readln(x[i])
end;
end;readvec
procedure writevec (var x:vec; name:char; n:int);
var i:int;
begin
writeln(' Вывести вектор ',name, ' размера n=', n); for i:=0 to n-1 do
begin
write (' ',name,'[',i:2,']='); writeln(x[i]:10:5)
end;
end;writevec
procedure readmatr(var y:matr; name:char; n,m:int);
var i,j:int;
begin
writeln (' Ввести матрицу ',name,
' размера : n=' ,n,', * m=' ,m); for i:=0 to n-1 do
for j:=0 to m-1 do
begin
write(' ',name, '[' ,i:2,' ,' ,j:2, ']= ');
readln (y[i,j])
end;
end;readmatr
procedure writematr(var y:matr; name:char; n,m:int);
var i,j:int;
begin
writeln (' Вывести матрицу ',name,
' размера: n=' ,n,', * m=' ,m);
for i:=0 to n-1 do
for j:=0 to m-1 do
begin
write(' ',name, '[' ,i:2,' ,' ,j:2, ']= ');
writeln (y[i,j]:8:4)
end;
end;writematr
procedure Em (var E:matr; n:int);
var i,j:int;
begin
for i:=0 to n do
for j:=0 to n do
if i=j then E[i,j]:=1 else E[i,j]:=0;
end;end E
procedure Rmatr(var a,b,c:matr; n,m:int);
var i,j:int;
begin
for i:=0 to n do
for j:=0 to m do
c[i,j]:=a[i,j]-b[i,j];
end;Rmatr
procedure obrmatr (Var AIS,AP: matr; n:int);
var i,j,k,l:integer;
a:matr;
begin
a:=AIS;
n:=n-1;
for k:=0 to n do begin
for j:=0 to n do
if (j<>k) then AP[k,j]:=-a[k,j]/a[k,k];
for i:=0 to n do
if (i<>k) then AP [i,k]:=a[i,k]/a[k,k];
for i:=0 to n do
for j:=0 to n do
if (i<>k) and (j<>k)
then AP[i,j]:= a[i,j]-a[i,k]*a[k,j]/a[k,k];
AP[k,k]:=1/a[k,k]; a:=AP;
end;
end; end obrmatr
procedure matrvec(var b:matr; var c,x:vec; n:int);
var i,j:int;
begin
for j:=0 to n-1 do begin
x[j]:=0;
for i:=0 to n-1 do
x[j]:=x[j]+b[i,j]*c[i]
end;
end; end matrvec
{ ТЕЛО ПРОГРАММЫ }
begin
clrscr;
readvec (c,'C',2);
readmatr (a,'A',2,2);
readmatr (a_1,'Z',2,2);
Em(e,2); rmatr(e,a,br,2,2); rmatr(e,a_1,br_1,2,2); obrmatr(br,b,2); obrmatr(br_1,b_1,2); matrvec (B,C,x,2); matrvec (B_1,C,x_1,2); matrvec (A,x,ax,2); matrvec (A_1,x_1,ax_1,2);
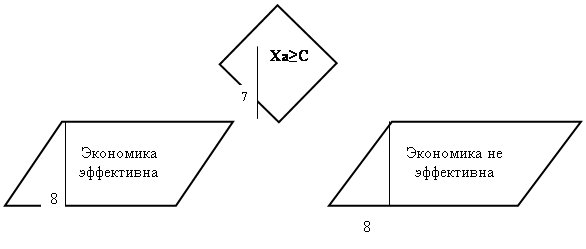
if (ax[0]<=c[0]) and (ax[1]<=c[1]) then
writeln (' Экономика матрица A - эффективна') else
writeln (' Экономика матрица A - не эффективна');
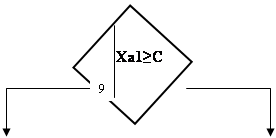
if (ax_1[0]<=c[0]) and (ax_1[1]<=c[1]) then
writeln (' Экономика матрица A_1 - эффективна') else
writeln (' Экономика матрица A_1 - не эффективна');
readln
write matr(B,’B’,2,2);
write matr (B1,’Z’,2,2);
write vec (x,’x’.2);
write vec(x1,’y’,2);
end.
{Окончание программы}
1.Процедура ввода вектора
| Ввод вектора X размерностью n | |
| Для I от n до n-1 с шагом 1 делать | |
| Ввести значение элемента массива X[i] | |
2.Процедура вывода вектора
| Вывод вектора X размерностью n | |
| Для i от 0 до n-1 с шагом 1 делать | |
| Вывести вектор X[i;j] | |
3.Процедура ввода матрицы
| Ввод размерности n,m ввод элементов массива Y[i;j] |
| ||
| Для i от 0 до n-1 с шагом 1 делать |
| ||
| Для i от 0 до m-1 с шагом 1 делать |
| ||
| Ввести значение элемента массива Y[i;j] | |||
4.Процедура вывода матрицы
| Вывод массива Y[i;j] размерностью n,m |
| ||
| Для i от 0 до n-1 с шагом 1 делать |
| ||
| Для i от 0 до m-1 с шагом 1 делать |
| ||
| Вывести массив Y[i;j] | |||
5.Процедура вывода единичной матрицы
| Вывод массива E[i;j] размерностью n | |
| Для i от 0 до n-1 с шагом 1 делать | |
| Для i от 0 до m-1 с шагом 1 делать | |
|
Да Нет | |
|
| |
| Вывести матрицу E [i;j] | |
6.Процедура умножения вектора на матрицу
| Для i от 0 до n-1 с шагом 1 делать | ||
| Для i от 0 до m-1 с шагом 1 делать | ||
| C[i;j]:=a[i;j]-b[i;j] | ||
7.Процедура умножения вектора на матрицу
| Для i от 0 до n-1 с шагом 1 делать | |
| X[i;j]:=0 | |
| Для i от 0 до n-1 с шагом 1 делать | |
| X[j]:=x[j]+c[i]*b[i;j] | |
8.Процедура образования матрицы
| А=ais;n:=n-1 | ||
| Для k от 0 до n с шагом 1 делать | ||
| Для i от 0 до n с шагом 1 делать | ||
| j≠k true | ||
| Ap[k;j]:=-a[k;j]/a[k;k] | ||
| Для I от 1 до n с шагом 1 делать | ||
| i≠k true | ||
| Ap[i;k]:=A [i;k]/A[k;k] | ||
| Для i от 0 до n с шагом 1 делать | ||
| Для j от 0 до nс шагом 1 делать | ||
| i≠k;j≠k true | ||
| AP[i;j]:=a[i;j]-a[i;j]*a[k;j]/a[k;k] | ||
| AP[k;k]:=1/a[k;k] | ||
| Q:=AP | ||
Расчеты при вводе значений
При добавлении:
B[0,0]=4.6154
B[0,1]=1,0462
B[1,0]=3,0769
B[1,1]=2,0308
Вывести матрицу Z размера :n=2,m=2
Z[0,0]=2,400
Z[0,1]=0,800
Z[1,0]=0,800
Z[1,1]=1,600
Вывести вектор Х размера n=2
Х[0]=13,84615
Х[1]=7,13846
Вывести вектор x размера n=2
Y[0]=4,8000
Y[1]=5,6000
Похожие работы
... в любой экономике. Представители неоклассической школы утверждают, что субъекты экономики ведут себя рационально и способны принимать решения, которые могут адекватно отразить основные тенденции развития макроэкономики в будущем. Они считают, что наемные работники с большой осторожностью относятся к резкому повышению своих номинальных доходов, такое увеличение является иллюзией, т.к. увеличение ...
... определённый момент времени (рублей, штук и т.п.). Изменение величины запаса за период, принимаемый за единицу времени есть величина потока. Уровень цен – одна из центральных категорий макроэкономики, с которой в микроэкономике определяются равновесные пропорции обмена благ, т.е. относительные (реальные) цены этих благ. Под уровнем цен понимается денежная оценка блага – или совокупности благ ...
... Вспомогательные финансовые институты. · Страховые компании и пенсионные фонды. Единство секторной классификации экономики во всех областях МФС позволяет обеспечить сопоставимость и согласованность статистических показателей. Время регистрации хозяйственной операции в международной МФС осуществляется на основе принципа начисления. Он заключается в том, что финансовые операции отражаются ...
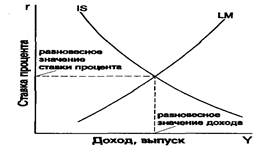
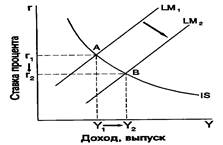
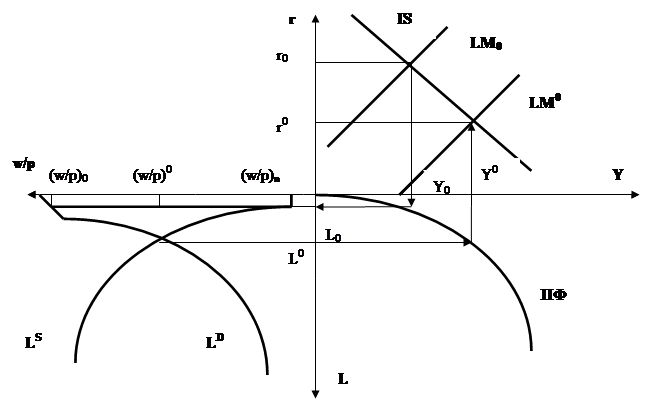
... на рабочую силу определяется фактически востребованным продуктом, и, значит, равновесие на рынке рабочей силы может быть достигнуто тогда, когда рынок товаров находится в равновесии. В целом модель Кейнса можно записать в следующем виде: Рынок рабочей силы: LS = LS (w / p), LD = LD(Y 0). (1.5) Рынок денег: M S= M S; M D= k * p * Y + Lq(r), < 0, ...

0 комментариев