Навигация
Введение.
Техническим приложением гидромеханики является наука гидравлика.
Гидравлика — это наука о законах движения и равновесия жидкостей и способах приложения этих законов к решению конкретных технических задач. С гидравликой связаны отрасли науки и техники, занимающиеся созданием, исследованием и использованием различных гидравлических машин: насосов, турбин, гидропередач и гидропривода. Часто описание теории этих машин, их устройства и принципов работы объединяют в одном учебном предмете «Гидравлика и гидравлические машины».
Слово гидравлика произошло от греческого hydro (вода) и aulos (трубка). В настоящее время это понятие значительно расширилось: гидравлика занимается изучением любой жидкости, движущейся не только в трубах.
В начале своего развития гидравлика представляла собой теоретическую науку — математическую механику жидкости или гидромеханику. Используя сложный математический аппарат и принимая некоторые допущения в отношении физических свойств жидкости, эта наука рассматривает движение жидкости по упрощенным схемам. Но методы математической гидромеханики не дали возможности решить целый ряд практических задач. В связи с этим стала развиваться практическая наука — техническая механика жидкости, решающая инженерные задачи методом упрощения гидравлических явлений, но с введением в теоретические уравнения поправочных коэффициентов, полученных в результате эксперимента.
В настоящее время приходится сталкиваться с задачами, при решении которых одновременно используются методы теоретической и технической гидромеханики. Поэтому различие в методах этих двух ветвей одной и той же науки постепенно исчезает. Современная гидравлика представляет собой самостоятельную, сформировавшуюся отрасль знаний, находящую применение в различных областях техники.
1. Краткая история развития гидромеханики.
Жизнь и деятельность человека во все времена были неразрывно связаны с водой. Еще в глубокой древности люди использовали реки и моря как пути сообщения и занимались орошением земель. Много лет назад в Средней Азии и Китае, Египте и Месопотамии, Риме и Греции были созданы различные гидротехнические сооружения для подъема и подачи воды: каналы и плотины, водоводы и акведуки. Во времена Траяна в Риме было 9 водопроводов общей длиной 436 км. Однако каких-либо сведений о гидравлических расчетах этих сооружений не найдено.
Первым научным трудом в области гидравлики принято считать трактат древнегреческого математика и механика Архимеда (ок. 287—212 до н. э.) «О плавающих телах», написанный примерно за 250 лет до н. э. Архимедом открыт закон о равновесии тела, погруженного в жидкость, который затем лег в основу теории плавания кораблей и их остойчивости.
Дальнейшее развитие гидравлика получила в XIV—XVII веках. Широко известны труды гениального итальянского ученого Леонардо да Винчи (1452—1519). Он изучал механизм движения жидкости в реках и каналах, процесс истечения жидкости, занимался постройкой гидротехнических сооружений, установил принцип работы гидравлического пресса, изобрел центробежный насос и многое другое. К этому же периоду относятся работы голландского инженера С. Стевина (1548— 1620); он определил давление жидкости на плоскость и описал гидравлический парадокс.
Итальянский ученый Г. Галилей (1564—1642) систематизировал основные положения гидростатики и впервые указал на зависимость гидравлических сопротивлений от скорости потока жидкости и его плотности, а его соотечественник Э. Торричелли (1608—1647) вывел формулу для расчета скорости истечения жидкости. Важное значение для гидравлики имели работы французского физика и математика Б. Паскаля (1623—1662), открывшего закон о передаче внешнего давления, носящий его имя.
Особо следует отметить работы выдающегося английского физика, математика, механика и астронома И. Ньютона (1643—1727), который впервые ввел понятие вязкости жидкости и установил зависимость между напряжением трения, градиентом скорости и свойствами жидкости; он же заложил основы теории гидродинамического подобия.
Исследования в этот период носили в основном теоретический характер и не были связаны друг с другом. Лишь во второй половине XVIII века труды крупнейших ученых-механиков и математиков, и прежде всего Д. Бернулли и Л. Эйлера, послужили теоретической основой гидромеханики и гидравлики.
Д. Бернулли (1700—1782) вывел основное уравнение движения жидкости. С именем Д. Бернулли связано понятие «гидродинамика»: в 1738 г. он опубликовал свою работу «Гидродинамика» — академический труд, выполненный автором во время работы в Петербурге.
Л. Эйлер (1707—1783)—знаменитый математик, механик, физик и астроном, уроженец Швейцарии. Не найдя на родине условий для научной деятельности, он в 1727 г. переехал в Россию и работал здесь до конца своих дней. Он опубликовал более 800 научных работ, относящихся к разным областям знаний, и создал основополагающий труд «Общие принципы движения жидкости».
Великий русский ученый М. В. Ломоносов (1711—1765), занимаясь общими проблемами физики, уделял большое внимание вопросам движения жидкостей и газов и практическому применению гидравлики, а открытый им закон сохранения массы и энергии лежит в основе современной гидравлики. М. В. Ломоносов поддерживал научные контакты с Л. Эйлером в период работы швейцарского ученого в Петербургской Академии наук.
Вторая половина XVIII и начало XIX века характеризуются ростом промышленного производства и бурным развитием техники. Для решения различного рода инженерных задач в области гидравлики требуются новые научные методы, учитывающие свойства реальной жидкости. Примерно в это время начинается второй период развития гидравлики — превращение ее в прикладную науку.
Большой вклад в становление технической гидромеханики внесли французские ученые А. Пито (1695—1771)—инженер-гидротехник, широко известный изобретением «трубки Пито», А. Шези (1718—1798), который вывел формулу для определения скорости движения жидкости, Ж. Борда (1733—1799), который вывел уравнение для определения потерь напора при резком расширении потока; итальянский профессор Д. Вентури (1746—1822), исследовавший процесс истечения жидкости из насадков; Д. Вейсбах (1806—1871) —крупный немецкий ученый, чьи теоретические и экспериментальные исследования в области движения жидкости не утратили своего значения до настоящего времени; английский ученый О. Рейнольдс (1842—1912), установивший два режима движения жидкости и критерий гидродинамического подобия;
Л. Прандтль (1875—1953), разработавший теорию турбулентных потоков.
Не остались в стороне от развития технической гидравлики и ученые России. Инженерное направление в гидромеханике интенсивно разрабатывалось в стенах Петербургского института путей сообщения, где была создана первая в России гидравлическая лаборатория и плодотворно работала группа ученых под руководством профессора П. П. Мельникова (1804—1880) — почетного члена Петербургской Академии наук, издавшего в 1836 г. первый на русском языке учебник по гидравлике «Основания практической гидравлики...». Выдающийся русский инженер, почетный член Петербургской Академии наук, профессор Н. П. Петров (1836—1920) на основе гипотезы Ньютона о трении в жидкости разработал гидродинамическую теорию смазки машин.
Особенно большой вклад в развитие гидравлики внес Николай Егорович Жуковский (1847—1921)—автор целого ряда работ по технической гидродинамике. Важнейшей его работой, вышедшей в свет в 1899 г., было исследование «О гидравлическом ударе».
В начале XX века в гидравлике стали формироваться различные направления специальных исследований. Характерной особенностью этого периода является проведение коллективных исследований и создание научных школ.
Талантливый . инженер и ученый В. Г. Шухов (1853—1939) разработал методы расчета нефтепроводов и изобрел оригинальное устройство для подъема нефти — эрлифт. Ведущую роль в разработке теории и расчета гидравлических сооружений сыграли работы Н. Н. Павловского (1884—1937).
С первых дней создания Советского государства наступил новый этап в развитии гидравлики в нашей стране. Разработка и осуществление плана ГОЭЛРО, проектирование и строительство крупных гидроэлектростанций потребовали решения целого ряда прикладных задач в области гидравлики, динамики русловых процессов и др. Были созданы специализированные научно-исследовательские и проектные институты, лаборатории при кафедрах некоторых ведущих высших учебных заведений. Ученые проводили исследования и изыскательские работы, необходимые для осуществления проектов строительства каналов им. Москвы, Беломоро-Балтийского, Волго-Донского им. В. И. Ленина, а также сооружения мощных гидроэлектростанций на Волге, Днепре, крупнейших реках Сибири.
Базой развития гидроэнергетики явилось создание в стране крупного энергетического гидромашиностроения, что позволило планомерно увеличивать единичную мощность гидроагрегатов на строящихся ГЭС. Так, на Волжской ГЭС им. XXII съезда КПСС мощность одной турбины составляет 115 МВт, на Братской— 250 МВт, на Красноярской — 500 МВт, на Саяно-Шушенской — 640 МВт. Не менее значительны достижения гидромашиностроения по разработке насосов высокого давления с большой подачей, объемного гидропривода и гидродинамических передач.
2.Гидравлика.
Похожие работы
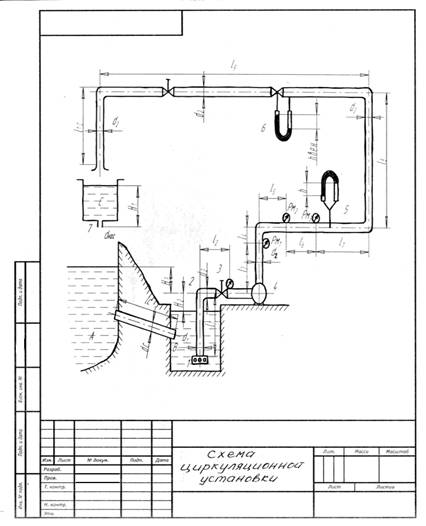
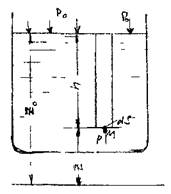
... 30 μвен 0,94 hвен, мм рт. ст 166 2, кг/м3 0 РВ, кПа 40 Рм1, кПа 145 dнас, мм 30 μнас 0,82 3. Схема установки 4. Расчет циркуляционной установки 4.1 Определение геометрической высоты всасывания насоса Н2 Для определения геометрической высоты воспользуемся известным уравнением Бернулли. Для его применения необходимо ...
... собой цель детального и всестороннего описания жидких тел, что подробно рассматривается в классическом курсе физики, напомним лишь некоторые положения, которые могут пригодиться при изучении гидравлики как самостоятельной дисциплины. Так, согласно молекулярно-кинетической теории строения вещества все физические тела в природе (независимо от их размеров) находятся в постоянном взаимодействии между ...
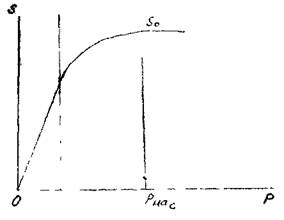
... . Для оценки режима течения жидкости вводят специальный критерий; число кавитации К f ' 7. Истечение жидкости из отверстий и насадков > 7.1. Отверстие в тонкой стенке Одной из типичных задач гидравлики, которую можно назвать задачей прикладного характера, является изучение процессов, связанных с истечением жидкости из отверстия в тонкой стенке и через насадки. ...
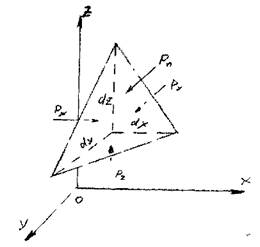
праведливы соотношения ... Пусть высота тетраэдра равна ... . Тогда его объём равен ... . Воспользуемся вторым законом Ньютона и со- ставим уравнение движения тетраэдра: ... ... где ... - ускорение центра масс тетраэдра. Переходя к пределу (устремляя ... ), получим ... Получим формулу Коши, утверждающую, что напряжения на гранях образуют систему взаимно уравновешенных ...
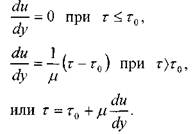
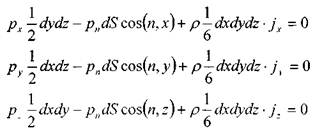
0 комментариев