Использование формул в сети Интернет

Использование формул в сети Интернет Какие бывают формулы Постановка задачи

56202

знака

таблицы

изображения

Отображение математических формул в формате LaTeX на форуме PHPBB3 Читать далее: Какие бывают формулы

2. Использование формул в сети Интернет

Естественнонаучные текстовые ресурсы

Важной особенностью многих образовательных и научных ресурсов являются специфические черты естественнонаучных текстов. Естественнонаучные тексты составляют огромную часть всего спектра электронных образовательных ресурсов, включая математику, физику, экономические науки, биологию и т.д.

Во многих естественнонаучных текстах одной из основных компонент являются математические формулы. Поэтому грамотная работа с формулами имеет ключевое значение для эффективной информационной поддержки многих направлений обучения.

Отметим, что математические формулы в виртуальном образовательном процессе могут использоваться более широко, чем просто в электронных текстах. Например, это могут быть форумы, чаты и другие формы обмена информацией в электронном виде, специализированные электронные практикумы по естественным наукам и т.д. – здесь также существуют проблемы, связанные с электронной обработкой математических формул. Развитие языков разметки и концепция разделения содержания и представления позволяют подойти к проблеме представления естественнонаучной информации комплексно и на основе стандартов.

Анализ существующих подходов

Классической средой работы с естественнонаучными текстами является система TeX, разработанная Д. Кнутом. Большой популярности TeX'а и его потомков (AMSTex, LaTeX и др.) способствовал ряд факторов. Во-первых, формализм ТеХ'а основан на идее разделения содержания и представления. Как правило, такого логического структурирования вполне достаточно, чтобы ТеХ сгенерировал полиграфический вариант текста высокого качества. Доводка внешнего представления текста имеющимися в TeX'е средствами полиграфической настройки может проводиться на втором этапе работы. Это наиболее перспективный подход, когда внешнее представление документа генерируется автоматически из логической разметки текста, сделанной человеком.

TeX является первой системой, в которой угадано основное направление развития представлений текстовой информации в распределенных информационных системах. Используемые в TeX'e, и особенно в его клонах, принципы разметки текста и отделения содержания от представления, лежат в основе современных подходов к обработке структурированной текстовой информации. Конечно, в ТеХ'е все эти возможности используются нерегулярно, и в незначительных масштабах. Кроме того, формализм ТеХ'а не соответствует современным формализмам разметки текстов, основанных на языке XML.

В последнее время для разработки математических текстов стал активно использоваться редактор MS Word, включающий специальные возможности для создания формул (MS Equation Editor, MathType). Подход, реализованный в этом редакторе, более доступен массовому пользователю, чем LaTeX, не требует установки дополнительного программного обеспечения. Минусы также очевидны. Во-первых, полиграфическое качество математических формул в Word'е значительно ниже, чем то, которое генерирует система ТеХ. Во-вторых, DOC-формат является принципиально закрытым форматом, мало пригодным для работы в открытых системах. Из этого, в частности, следует непригодность DOC-формата для публикации информации в Интернете – приходится конвертировать текст либо в HTML (причем хорошо известна колоссальная перегруженность структуры HTML-файла, который генерируется Вордом), либо в другой закрытый, но более приспособленный для обмена формат PDF. Есть и другие довольно существенные недостатки. Вообще, с точки зрения современного понимания того, как работать со структурированной текстовой информацией, идеология, заложенная в редакторе Word, является значительно более устаревшей, чем в появившейся намного раньше системе TeX.

Отметим и другую проблему. Наличие нескольких стандартов представления математических и естественнонаучных текстов вносит очень серьезную путаницу. Например, уже сегодня многие сталкиваются с той проблемой, что организаторы разных научных конференций требуют тексты в разных форматах – кто-то в LaTeXе, кто-то в Word'е. Информационная среда заполняется информацией, сформатированной в совершенно разных, несовместимых стандартах. Результат – потеря целостности информационной среды, постоянные проблемы с чтением, использованием и обработкой текстов в разных форматах.

К настоящему времени созданы все необходимые технологические условия для решения этих проблем. Созданы нужные открытые стандарты как для работы с текстами произвольного характера, так и для представления таких специфических объектов, как математические формулы. В частности, можно говорить и о решении вышеперечисленных проблем через создание «канонического» формата представления математических и естественнонаучных текстов на основе имеющихся сегодня открытых стандартов. Канонический формат представления научных и образовательных текстов, это такой формат, который

1. базируется на принципе разделения представления и содержания документа.

2. основан на разметке текстов логического уровня.

3. использует для представления документов открытые широко признанные стандарты.

4. удобен для автоматической обработки, распространения и хранения информации.

5. предоставляет возможность конверсии текстов, представленных в каноническом формате, в другие распространенные форматы представления естественнонаучной информации и обратно.

6. допускает трансляцию в различные (поли) графические представления, как электронные, так и бумажные.

7. допускает богатую «интеллектуальную» обработку документа достаточно легкими онлайновыми программными средствами.

Базой для создания такого формата служит расширяемый язык разметки XML. Очень существенным шагом в этой области является появление диалекта XML – языка MathML, ориентированного на описание математических формул. MathML интересен по многим причинам. Во-первых, формат MathML основан на языке разметки XML, что позволяет использовать большое количество наработанных компонент и библиотек. Во-вторых, формат MathML реализует два вида представления: презентационное и содержательное. В-третьих, формат MathML является открытым стандартом, поддерживаемым консорциумом W3, что очень важно для построения сложных систем, ориентированных на использование широкими массами пользователей. В своей «презентационной» части MathML идеологически весьма близок TeX-формату.

С учетом вышеперечисленных плюсов, оптимальным решением является принятие формата MathML в качестве канонического формата обработки и представления математических формул. Вообще, когда говорят об обработке математических формул, то подразумевают всю цепочку: ввод формул пользователем, хранение формул, обработка формул, отображение формул.

Когда речь идет о вводе формул пользователем, то можно рассматривать две основные ситуации: создание, редактирование и представление математических текстов, и ввод формул в различных прикладных приложениях и Web-сервисах, в частности, электронных форумах и учебных программных комплексах. Решение задач обработки естественнонаучной информации является самостоятельной и весьма объемной проблемой.

TeX

T_EΧ (обычным текстом – TeX) – система компьютерной вёрстки, разработанная американским профессором информатики Дональдом Кнутом в целях создания компьютерной типографии. В неё входят средства для секционирования документов, для работы с перекрёстными ссылками и для набора сложных математических формул.

Название произносится как «тех» (от греч. τέχνη – «искусство», «мастерство»). В написании буква E опущена ниже T и X.

Документы набираются на собственном языке разметки в виде обычных ASCII-файлов, содержащих информацию о форматировании текста или выводе изображений. Эти файлы (обычно имеющие расширение «.tex») транслируются специальной программой в файлы «.dvi» (device independent – «независимые от устройства»), которые могут быть отображены на экране или напечатаны. DVI-файлы можно специальными программами преобразовать в PostScript, PDF, или другой электронный формат.

Ядро TeX’а представляет собой язык низкоуровневой разметки, содержащий команды отступа и смены шрифта. Огромные возможности в TeX’е предоставляют готовые наборы макросов и расширений. Наиболее распространённые расширения стандартного ТеХ’а (наборы шаблонов, стилей и т.д.): LaTeX (произносится «лате́х») и AMS-TeX. При использовании пакета расширения LaTeX можно превратить разросшуюся статью в книгу изменением одного слова в исходнике, вставлять оглавление одной командой, не задумываться о нумерации разделов, теорем, рисунков. Есть много пакетов для оформления химических формул (например, пакет XymTeX), диаграмм (xypic), создания презентаций и визитных карточек и тому подобного.

Распространённые комплекты вёрстки на основе ТеХ’а: для Windows – TeX Live или MikTeX, для UNIX-подобных систем – TeX Live или teTeX.

Для создания шрифтов совместно с TeX’ом используется специально разработанная система METAFONT, в которой шрифты описываются программами на специализированном языке Meta. Могут также использоваться векторные шрифты в формате PostScript Type 1, TrueType и OpenType.

T_EΧ применяется в исходных текстах Википедии для набора математических формул.

История

Первый том книги «Искусство программирования» Д. Кнута был опубликован в 1969 году и печатался методом монотипии, технологии XIX века, которая давала на выходе издание в «хорошем классическом стиле», что нравилось Кнуту. Когда в 1976 году публиковалось второе издание второго тома, всю книгу пришлось набирать вновь, поскольку монотипия почти повсеместно была замещена фотографической техникой, и оригинальные шрифты больше не использовались. Однако, когда 30 марта 1977 года Кнут получил новые оттиски, он увидел что они выглядят ужасно. Примерно в это же время Кнут впервые увидел результат работы высококачественной цифровой типографической системы, и заинтересовался возможностями цифровой типографии. Не оправдавшие ожиданий оттиски дали ему дополнительный толчок к тому чтобы решить проблему раз и навсегда, разработав свою типографическую систему. 13 мая 1977 года он написал заметку самому себе, описывающую базовые возможности TeX.

Он планировал завершить систему в свой творческих отпуск 1978 года, но получилось так что язык был зафиксирован лишь в 1989 году, более 10-ти лет спустя. Летом 1978 года, когда Кнут писал первую версию TeX, Guy Steele был в Стэнфорде; осенью того же года он вернулся в МТИ и переписал систему ввода / вывода TeX под операционную систему ITS. Первая версия TeX была написана на языке программирования SAIL и работала на PDP-10 под операционной системой WAITS. Для следующих версий Кнут изобрёл концепцию «грамотного программирования» (англ. literate programming), способ получения совместимого исходного кода и документации к нему (в виде текста на TeX, конечно) из одного и того же оригинального файла. Этот язык был назван WEB и производил программы на Паскале.

Новая, переписанная с нуля версия TeX была издана в 1982 году и названа TeX82. Помимо других изменений, первоначальный алгоритм переносов был заменён новым, написанным Frank Liang. TeX82 также использовал арифметику с фиксированной запятой вместо арифметики с плавающей запятой, с тем чтобы обеспечить воспроизводимость результата на различном оборудовании. Помимо этого, под нажимом Guy Steele, в TeX82 появился настоящий, тьюринг-полный язык программирования.

В 1989 году Дональд Кнут выпустил новую версию TeX и METAFONT.

MathML

MathML (от англ. Mathematical Markup Language, язык математической разметки) – это приложение XML, используемое для представления математических символов и формул в документах WWW. MathML рекомендован математической группой W3C.

Спецификация MathML версии 1.01 вышла в июле 1999, в феврале 2001 появилась версия 2.0. В октябре 2003 была опубликована вторая редакция MathML версии 2.0, которая является на настоящий момент последней спецификацией, выпущенной математической группой W3C.

MathML рассматривает не только представление, но и смысл элементов формулы. Также разрабатывается система разметки математической семантики, призванная дополнить MathML. Она называется OpenMath.

MathML имеет 2 версии – Presentation MathML и Content MathML.

Пример:

В TeX описание

x = \frac {-b \pm \sqrt {b^2 – 4ac}} {2a}

используется для представления формулы

$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$

Ниже приведено описание этой формулы с помощью MathML:

<mrow>

<mfrac>

<mrow>

</mrow>

<mo>&PlusMinus;</mo>

<msqrt>

<mrow>

<msup>

</msup>

<mrow>

</mrow>

</msqrt>

</mrow>

<mrow>

</mrow>

</mfrac>

</mrow>

XML-структура MathML обеспечивает широкую область использования и позволяет быстро отображать формулы в приложениях, таких как браузеры, а также легко интерпретировать их значения в математических программных продуктах.

Поддержка программного обеспечения

Существует множество утилит для преобразования математических выражений в MathML, включая конвертеры между TeX и MathML.

Основными браузерами, непосредственно поддерживающими MathML, являются последние версии Mozilla и его разновидности. Начиная с бета-сборки 9656 (от 16 ноября 2007), этот язык поддерживает также Opera. Многие другие браузеры поддерживают этот формат при установке соответствующих плагинов. Например, в Internet Explorer для поддержики MathML используется плагин MathPlayer.

Кроме того, MathML поддерживается основными офисными программами, такими как Microsoft Word и OpenOffice.org, а также математическими программными продуктами, например, Mathematica, Maple.

Ряд решений

Рассмотрим 2 варианта решения проблемы отображения формул на конкретных примерах.

Википедия (http://ru.wikipedia.org)

Для математических формул MediaWiki использует разметку TeX'а. Но, в зависимости от пользовательских настроек и сложности выражения, они могут отображаться либо как PNG-рисунки, либо в обычной HTML-разметке.

Общие положения

· Исходный код математической формулы записывается внутри тега <math>…</math>.

· Шаблоны, переменные и параметры MediaWiki не функционируют внутри этого тега.

· Пробелы игнорируются (ТеХ их сделает сам).

· Пустые строки не разрешаются.

· Буквы должны быть набраны только латинским шрифтом. В случае написания даже одной буквы кириллицей программа сообщает об ошибке.

· Каждая буква считается переменной и воспроизводится курсивом, а цифры – прямым шрифтом (исключение – название функций и операций). Чтобы не допустить курсивного начертания для прочего текста, используйте команды \mbox или \mathrm. Например, запись <math>\mbox{abc}_\mathrm{def}</math> отображается как abc_def.

· Символы записываются с помощью «команд»^[2], которые начинаются с «обратного слэш» (\) и состоят либо из командного слова из латинских букв, либо из символа (не буквы). В первом случае после командного слова должен быть обязательно пробел или другая команда.

· Команды могут иметь аргументы: {обязательные} и [необязательные].

· Переводы строк внутри тега <math>…</math> не отображаются, поэтому, чтобы сделать код более читабельным, можно вставлять переводы строк после каждого выражения или строки матрицы.

· Если в настройках пользователя не выбрана опция «Всегда генерировать PNG», то простые формулы будут отображаться как в HTML-разметке. Чтобы заставить их всегда отображаться как PNG-рисунки, следует в начале или в конце формулы вставить один из знаков принудительного пробела (~ \, \!). Cравните:

<math>a (1 + e^2 / 2)</math> a (1 + e² / 2)

<math>df(x) = f'(x) dx</math> df(x) = f'(x) dx

$df(x) = f'(x)dx\,$

· Чтобы создать выражения вида $A\stackrel{f}{\longrightarrow}B$ , используйте команду \stackrel{выражение1} {выражение2}, где выражение1 – то, что будет отображаться над строкой, выражение2 – то, что останется в строке. Код приведённой формулы:

<math>A\stackrel{f} {\longrightarrow} B</math>.

· Десятичную запятую в десятичных дробях рекомендуется заключать в фигурные cкобки, чтобы избежать ненужного тонкого пробела после запятой. Сравните:

<math>~\pi=3,1415\dots</math>	$~\pi=3,1415\dots$
<math>~\pi=3 {,} 1415\dots</math>	$~\pi=3{,}1415\dots$

Исходные команды Служебные значки

· \ сигнальный символ (команд);

· {начало группы;

· } конец группы;

· _ нижний индекс;

· ^ верхний индекс;

· ~ неразрывный пробел.

Шрифты

Буква	Команда	Буква	Команда	Буква	Команда
$\Alpha~\alpha$	\Alpha \alpha	$\Iota~\iota$	\Iota \iota	$\Sigma~\sigma$	\Sigma \sigma
$\Beta~\beta$	\Beta \beta	$\Kappa~\kappa$	\Kappa \kappa	$~\varsigma$	\varsigma
$\Gamma~\gamma$	\Gamma \gamma	$\Lambda~\lambda$	\Lambda \lambda	$\Tau~\tau$	\Tau \tau
$\Delta~\delta$	\Delta \delta	$\Mu~\mu$	\Mu \mu	$\Upsilon~\upsilon$	\Upsilon \upsilon
$\Epsilon~\epsilon$	\Epsilon \epsilon	$\Nu~\nu$	\Nu \nu	$\Phi~\phi$	\Phi \phi
$~\varepsilon$	\varepsilon	$\Xi~\xi$	\Xi \xi	$\varphi$	\varphi
$\Zeta~\zeta$	\Zeta \zeta	$\Pi~\pi$	\Pi \pi	$\Chi~\chi$	\Chi \chi
$\Eta~\eta$	\Eta \eta	$\varpi$	\varpi	$\Psi~\psi$	\Psi \psi
$\Theta~\theta$	\Theta \theta	$\Rho~\rho$	\Rho \rho	$\Omega~\omega$	\Omega \omega
$\vartheta$	\vartheta	$\varrho$	\varrho

С помощью соответствующих команд можно изменять вид шрифта (гарнитуру) и его размеры:

Вид шрифта	Команда	Изображение
Жирный шрифт (греческий)	\boldsymbol	$\boldsymbol{\alpha}+\boldsymbol{\beta}+\boldsymbol{\gamma}$
Жирный шрифт (векторы)	\mathbf	$\mathbf{x}\cdot\mathbf{y} = 0$
Ажурный шрифт	\mathbb	$\mathbb{NQRC}$
Рубленый шрифт	\mathsf	$\mathsf{PMEDV}$
Готический шрифт	\mathfrak	$\mathfrak{a} \mathfrak{A} \mathfrak{B}$
Рукописный шрифт	\mathcal	$\mathcal{ABC}$
Прямой шрифт	\mathrm	abcd
Прописные наклонным шрифтом	\mathit	$\mathit\Gamma~\mathit\Theta~\mathit\Sigma$

Бинарные операции

Команда	Изображение
+ –	$+ \; -$
\amalg \setminus	$\amalg \; \setminus$
\pm \mp	$\pm \; \mp$
\ast \star *	$\ast \; \star \; *$
\centerdot \cdot \bullet	$\centerdot \; \cdot \; \bullet$
\circ \bigcirc	$\circ \; \bigcirc$
\odot \circleddash \circledast \circledcirc	$\odot \; \circleddash \; \circledast \; \circledcirc$
\oplus \otimes \ominus \oslash	$\oplus \; \otimes \; \ominus \; \oslash$
\boxplus \boxtimes \boxminus \boxdot	$\boxplus \; \boxtimes \; \boxminus \; \boxdot$

Команда	Изображение
\sqcap \sqcup	$\sqcap \; \sqcup$
\cap \cup \uplus	$\cap \; \cup \; \uplus$
\Cap \Cup	$\Cap \; \Cup$
\doublecap \doublecup	$\doublecap \; \doublecup$
\dagger \ddagger	$\dagger \; \ddagger$
\times \div \divideontimes	$\times \div \divideontimes$
\ltimes \rtimes	$\ltimes \; \rtimes$
\leftthreetimes \rightthreetimes	$\leftthreetimes \; \rightthreetimes$
\vartriangle \triangledown	$\vartriangle \; \triangledown$
\triangle \mathcal 5	$\triangle \; \mathcal 5$

Команда	Изображение
\bigtriangleup \bigtriangledown	$\bigtriangleup \; \bigtriangledown$
\triangleright \triangleleft	$\triangleright \; \triangleleft$
\diamond	$\diamond$
\bowtie	$\bowtie$
\vee, \lor \wedge, \land	$\vee \; \lor \; \wedge \; \land$
\veebar \barwedge	$\veebar \; \barwedge$
\doublebarwedge	$\doublebarwedge$
\curlywedge \curlyvee	$\curlywedge \; \curlyvee$
\wr	$\wr$
\intercal	$\intercal$
\dotplus	$\dotplus$

Символы математических функций

При написании стандартных функций обратите внимание:

Правильно:	<math>\sin x + \ln y +\operatorname{sgn}\, z</math>	$\sin x + \ln y +\operatorname{sgn}\, z$
Неправильно:	<math>sin x + ln y + sgn z</math>	$sin x + ln y + sgn z\,$

Тригонометрические
\sin	$~\sin$
\cos	$~\cos$
\tan	$~\tan$
\cot	$~\cot$
\sec	$~\sec$
\csc	$~\csc$
\arcsin	$~\arcsin$
\arccos	$~\arccos$
\arctan	$~\arctan$
\arccot	$~\arccot$
\arcsec	$~\arcsec$
\arccsc	$~\arccsc$

Гиперболические
\sinh	$~\sinh$
\cosh	$~\cosh$
\tanh	$~\tanh$
\coth	$~\coth$
Прочие
\arg	$~\arg$
\deg	$~\deg$
\det	$~\det$
\dim	$~\dim$
\exp	$~\exp$
\lg	$~\lg$
\ln	$~\ln$
\log	$~\log$

\max	$~\max$
\min	$~\min$
\mod	$a \mod b$
\bmod	$~a \bmod b$
\pmod	$~a \pmod b$
\gcd	$~\gcd$
\hom	$~\hom$
\inf	$~\inf$
\ker	$~\ker$
\lim	$~\lim$
\liminf	$~\liminf$
\limsup	$~\limsup$
\Pr	$~\Pr$
\sup	$~\sup$

Электронная библиотека Попечительского совета механико-математического факультета МГУ (http://lib.mexmat.ru)

На форуме появился новый тег \math. Если окружить парой таких тегов формулу в TeX'е, то в сообщение автоматически будет помещена картинка с написанной формулой. Примерно так: пишете

Код:

[math]$n \in \mathbb{N}$[/math]

и в сообщении появляется вот такая картинка: $n \in \mathbb{N}$ .

А при наведении на нее указателя мышки можно увидеть исходный код картинки, то есть то, что заключено между тегами math.

Теперь размеры картинок регулируемы. Этот параметр можно изменять в собственном профиле. Для Гостей этот параметр неизменяем.

Quick Start для тех, кто пользуется MathType.

Последовательность действия для использования MathType такая:

1) набрать формулу в MathType

2) (требуется выполнять только первый раз – затем настройки сохранятся и этот пункт можно пропускать)

a) В меню MathType Preferences выбрать Translators. В открывшемся окне в меню «Translator» выбрать один из TeX-трансляторов (например «TeX – AMS-LateX»)

б) убрать галочку с «Include MathType data in translation»

3) Скопировать формулу

4) Вставить в окно ввода в форуме

5) Выделить вставленный текст и нажать кнопку Math. Ура – формула готова.

Вот пример, генерированный MathType:

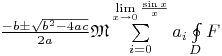
$\frac{{ - b \pm \sqrt {b^2 - 4ac} }}{{2a}}\mathfrak{M}\sum\limits_{i = 0}^{\mathop {\lim }\limits_{x \to 0} \frac{{\sin x}}{x}} {a_i } \oint\limits_D F$

Упрощенная форма записи формул в сообщениях.

1. Последовательность $…$ теперь автоматически окружается тегом math, если содержимое не разбито переносом строки.

2. Последовательность $$…$$ теперь тоже автоматически окружается тегом math.

3. Пункты 1 и 2 не выполняются, если указанные последовательности находятся внутри тегов math или code

4. Для отмены автозамены (в случае, когда Вы хотите употребить знак доллара в его обычном смысле) заключите Ваше сообщение в тег <notex>…</notex> (скобки замените на квадратные)

Как писать формулы.

Тег math преобразует содержимое в картинку, которая получилась бы, если бы мы составили LaTeX-документ с такой преамбулой:

Код:

\documentclass{article}
\usepackage{amsmath}
\usepackage {amsfonts, amssymb}
\usepackage{amsthm}
\usepackage[cp1251] {inputenc}
\usepackage [matrix, arrow, curve] {xy}
\usepackage [english, russian] {babel}
\usepackage[final] {graphicx}
\usepackage{mathrsfs}
\pagestyle{empty}
\begin{document}

Отображение математических формул в формате LaTeX на форуме PHPBB3 Читать далее: Какие бывают формулы

Раздел: Информатика, программирование
Количество знаков с пробелами: 56202
Количество таблиц: 22
Количество изображений: 2

Скачать

Главная Новости Рефераты Статьи Вузы

О проекте Соглашение

Наверх

Войти на сайт

Навигация

0 комментариев

Разделы

Инфо

Следите за новостями