Навигация
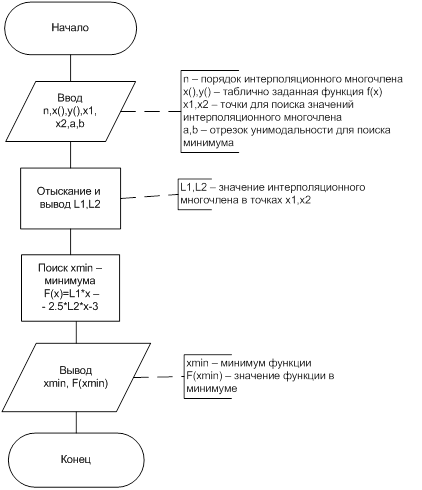
Программа вычисления минимума заданной функции
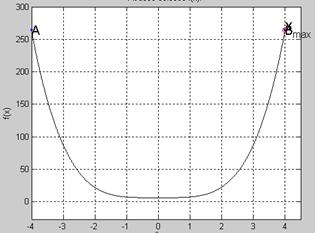
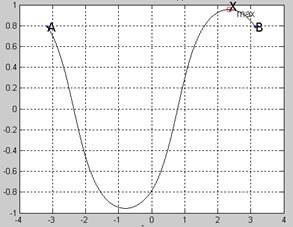
Вычислить минимум функции F(x)=L(x1)x2-2.5L(x2)x-3 на отрезке [a;b] с точностью ε.
L(x1), L(x2) значения интерполяционного многочлена, построенного для таблично заданной функции f(x) в точках x1, x2.
Исходные данные:
a=0; b=2;
x1=0.041770;
x2=0.587282;
ε=10-4;
| x | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 |
| f(x) | 1.858652 | 1.851659 | 1.851401 | 1.848081 | 1.841914 | 1.833125 | 1.821948 |
2. Постановка задачи и формализация
Для решения поставленной задачи необходимо разработать программные модули, выполняющие следующие действия:
- главный модуль, получающий исходные данные (таблично заданную f(x), a, b, x1, x2, ε), передающий их на обработку и выводящий промежуточные и конечные результаты (L(x1), L(x2), найденный минимум функции)
- модуль поиска значения интерполяционного многочлена L(x1), L(x2)
- модуль поиска минимума функции F(x) численным методом, использующий L(x1), L(x2) как коэффициенты при x2 и x
3. Выбор, обоснование, краткое описание методов
3.1 Поиск значений интерполяционного многочлена в точках x1 и x2
3.1.1 Постановка задачи
Требуется найти L(x1), L(x2) - значения интерполяционного многочлена, построенного для таблично заданной функции f(x) в точках x1,x2 Здесь решается задача аппроксимации, которая состоит в замене некоторой функции
у = f(х) другой функцией g(х,а0,а1,...,an) таким образом, чтобы отклонение g(х,а0,а1,...,an) от f(x) удовлетворяло в некоторой области (на множестве X) определенному условию. Этим условием является g(xi,a0,a1,…an)=f(xi) при i=0,n, которое означает, что аппроксимируемая функция f(x) совпадает с g(xi,a0,a1,…an) в т.н. узлах интерполяции x0,x1,…,xn. Это частный случай аппроксимации, называемый интерполяцией.
3.1.2 Выбор и описание метода
Задача интерполяции может быть решена множеством методов, среди которых:
1) интерполяционный многочлен Лагранжа
интерполяционные формулы Ньютона Выберем для решения задачи интерполяции интерполяционный многочлен Лагранжа, так как его построение просто в алгоритмизации, не требует вычисления конечных разностей функции, , может быть умещено в одну небольшую процедуру – функцию.
Кроме того, метод Лагранжа работает и для неравноотстоящих интерполяционных узлов, к тому же не имеет различий, если точки x1 и x2 для поиска значений L(x1), L(x2) лежат в начале или в конце отрезка, где таблично задана функция.
Описание метода:
Задача интерполяции будем решать построением многочлена Лагранжа, который имеет вид:

Степень многочлена n обеспечивается n+1 интерполяционным узлом. Для задания таблицы значений функции будем использовать два массива x() и y(). Полином должен удовлетворять условию Ln(xi)=y(i)
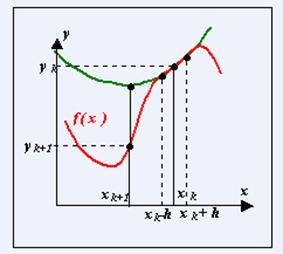
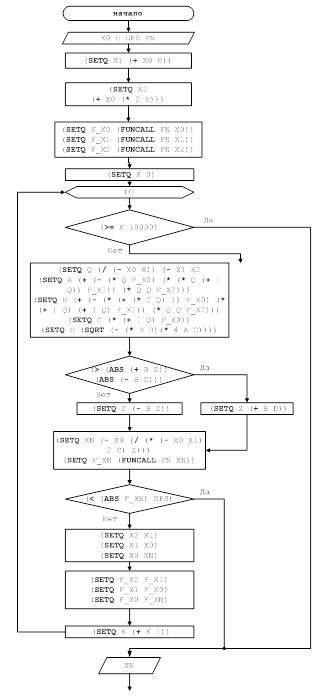
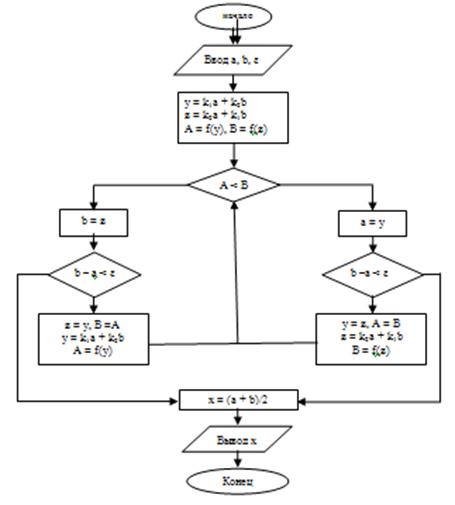
3.2 Поиск минимума функции F(x) на отрезке [a;b]
Похожие работы
... , так и их реализации с помощью конкретных инструментов – сред и языков программирования. Итогом работы можно считать созданную функциональную модель вычисления минимума заданной функции методом парабол. Данная модель применима к детерминированным задачам, т.е. погрешностью экспериментального вычисления функции f(x) можно пренебречь. Созданная функциональная модель вычисления минимума заданной ...
... исследованных функций. Так же необходимо изучить работу встроенных в MatLab функций. Протестировать программу на серии тестов. Теоретическое описание Одномерная оптимизация функций методом золотого сечения Метод золотого сечения состоит в построении последовательности отрезков [a0, b0], [a1, b1], …,стягивающихся к точке минимума функции f(x). На каждом шаге, за исключением первого, вычисление ...
... все многообразие факторов, имеющих место в реальных системах, т. е. использованию моделей, более адекватных исследуемым явлениям. Библиографический список 1 Лященко И.Н. Линейное и нелинейное программирования / И.Н.Лященко, Е.А.Карагодова, Н.В.Черникова, Н.З.Шор. – К.: «Высшая школа», 1975, 372 с. 2 Методические указания для выполнения курсового проекта по дисциплине «Прикладная ...
... диаграммы. С этой целью строки и столбцы таблицы переставляются до тех пор, пока не получится упорядоченная диаграмма. Поиск сегментов рынка для программы установки защищенных сетевых соединений с помощью протокола ISAKMP Взрывной характер развития компьютерных технологий и резко возросшее количество действий совершаемых с помощью глобальной сети Internet (развитие электронной торговли, ...
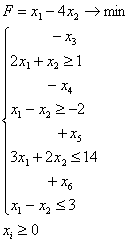
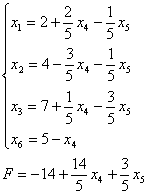
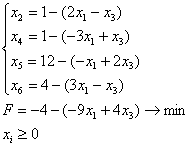
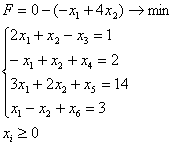

0 комментариев