Навигация
Линейные конечно-разностные уравнения и их применение в экономике
29316
знаков
5
таблиц
6
изображений
1.3 Линейные конечно-разностные уравнения и их применение в экономике
Динамика объектов различной природы часто описывается уравнениями вида
xt = F(xt-1, xt-2, ... , xt-n),(7)
связывающими состояние объекта xt в любой момент времени t с состояниями в предшествующие моменты времени. Решение уравнения (7) n-го порядка определено однозначно, если заданы n так называемых начальных условий. Обычно в качестве начальных условий рассматриваются значения xt при t = 0, 1,..., n - 1.
Подставляя начальные значения xn-1, ... , x1, x0 и t = n в качестве аргументов функции в правой части (7), находим xn; используя найденное значение и подставляя теперь xn, xn-1, ... , x2 x1 и t = n + 1 в качестве аргументов функции, находим xn+1, и т.д. Процесс может быть продолжен до тех пор, пока не будут исчерпаны все представляющие интерес значения t.
В модели экономических циклов Самуэльсона-Хикса используются конечно-разностные уравнения вида xt = a1xt-1 + a2xt-2 + f(t) - линейные конечно-разностные уравнения второго порядка, являющиеся частным видом уравнения (7). Они называются однородными, еслиf(t) = 0 при любых t, неоднородными - в противном случае. И для нахождения, и для исследования свойств решения однородного уравнения
xt = a1xt-1 + a2xt-2 ,(8)
используется так называемое характеристическое уравнение
- a1
- a2 ,(9) 
Обозначим его корни 
1, 2 и запишем
В теории конечно-разностных уравнений[4] доказывается, что при 1
2 решение уравнения (8) описывается равенством
, (10)
где A1 и A2 - постоянные, определяемые начальными условиями.
Если же 
1 = 2 = , то решение имеет вид
, (11)
Решение уравнения (8) зависит от значения дискриминанта 
характеристического уравнения (9).
Рассмотрим возникающие при этом случаи.1. D > 0. Характеристическое уравнение имеет два различных вещественных корня. Решение описывается равенством (10); если оба корня положительны, то обе компоненты решения - монотонные геометрические прогрессии. Если имеются отрицательные корни, то каждому из них отвечает знакочередующаяся составляющая решения (10).2. D = 0. Характеристическое уравнение имеет совпадающие вещественные корни, и решение имеет вид (11).
3. D < 0. Характеристическое уравнение имеет пару сопряженных комплексных корней: 1,2 = 
i
.
Равенство (10) при этом справедливо, но неудобно для использования, так как вещественный процесс при этом описывается как сумма комплексных составляющих. Более удобную форму решения можно получить, используя тригонометрическое представление корней: 1,2 = g(cos
sin), где 
Такое представление позволяет описать решение уравнения (8) равенством
, (12)
где B1 и B2 - постоянные, определяемые начальными условиями.
Таким образом, при D < 0 решение носит характер колебаний, амплитуда которых возрастает (при g > 1) или убывает (при g < 1);
Решение уравнения (8) называют равновесным, если значение xt не изменяется во времени. Подстановкой в уравнение (8) можно убедиться, что xt = 0 есть равновесное решение. Равновесное решение называется устойчивым, если xt
0 при t 
; в противном случае оно называется неустойчивым. Равенства (10) и (11) показывают, что решение будет устойчивым в том и только в том случае, если оба корня характеристического уравнения по модулю меньше единицы. В случае D < 0 условию устойчивости соответствует g < 1, так как 
при этом необходимым и достаточным условием устойчивости является a2 > -1. По теореме Виета 
12 = -a2, так что условие a2 > -1 необходимо и в случае D > 0, но здесь оно не является достаточным. Система неравенств
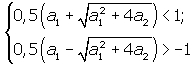
дает необходимое и достаточное условие устойчивости для данного случая. Для этого требуется, чтобы выполнялось неравенство 
Систему можно заменить одним неравенством
Объединяя все полученные результаты, условие устойчивости можно представить в виде двойного неравенства
,(13)
Уравнение модели экономических циклов Самуэльсона-Хикса имеет вид уравнения (8), при этом 
Заметим, что Cy
0 и 
Похожие работы
... ства и инвестиций, которое усугубляется кризисом доверия к кредитной сфере. Третий вид теории, выводящей циклические колебания экономики из свойств экономического субъекта, представляет собой «равновесная теория экономического цикла» Р. Лукаса. Эта теория основана не на анализе каких-либо реальных особенностей психологии участников производства. Главную роль в этой концепции играет гипотеза о ...
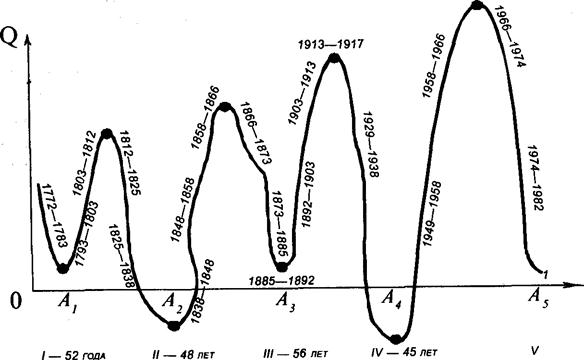
... литературе концепция больших экономических циклов рассматривается применительно к проблеме макроэкономического прогнозирования. Доминирующее место в теориях экономических циклов зан6имают проблемы проявления среднесрочных экономических циклов. 3. ГОСУДАРСТВЕННОЕ АНТИЦИКЛИЧЕСКОЕ РЕГУЛИРОВАНИЕ В преодолении кризиса в современных условиях значительную роль играет антикризисная ...
... того, как реагируют переменные равновесной системы на изменения ее параметров; именно эти изменения в параметрах и обусловливают колебания в системе, характеризующейся равновесием. Далее Самуэльсон изложил теорию потребительского спроса и производства в категориях предпочтений, как их толкуют ординалисты. Однако, хотя Самуэльсон утверждал, что рациональный элемент поведения в нормативном смысле ...
... последующего восстановления макроэкономического равновесия (расширения и сжатия общественного воспроизводства) любой конкретный цикл (национальный или мировой) и каждый конкретный кризис требует дифференцированного анализа породивших его внутренних и внешних факторов. 2. Экономическая политика: истоки формирования Для развития рыночной экономики характерна такая закономерность как тенденция ...
0 комментариев