Навигация
Симплексная таблица( опорный план в виде симплекс таблицы)
5157
знаков
4
таблицы
0
изображений
1 симплексная таблица( опорный план в виде симплекс таблицы)
| Оценка базисных переменных | Базисные переменные | Свободные члены | 5 | 6 | 0 | 0 | 0 |
| С | Х | Р0 | Р1 | Р2 | Р3 | Р4 | Р5 |
| 0 | Х3 | 606 | 9 | 27 | 1 | 0 | 0 |
| 0 | Х4 | 802 | 15 | 15 | 0 | 1 | 0 |
| 0 | Х5 | 840 | 15 | 3 | 0 | 0 | 1 |
| С | 0 | -5 | -6 | 0 | 0 | 0 | |
Переход к новому опорному плану, выбор разрешающего столбца:
СК=мин{Сj(cj|<0)}=мин {-5; -6 }=-6=С2=К=2
Выбор разрешающей строки:
bl/ alk=min {bi/ai2(ai2>0)} min{606/27;802/15;840/3}={22;53;280} =22=b1/a12=l=1
Генеральный элемент: alk=а12=27
Переход к новой симплексной таблице:
B1= b1/ а12=606/27=22
c=C-ckbс=c-c2b1=0-(-6)*22=132
alj=alj/alk
9/27=1/3
27/27=1
=1/27
=0/27=0
0/27=0
-5-(-6)*1/3=-3
-6-(-6)*1=0
0-(-6)*1/27=2/9
0-(-6)*0=0
0-(-6)*0=0
=802-15*22=472
=840-3*22=774
15-15*1/3=10
15-15*1=0
0-0*1/27=0
1-1*0=1
0-0*0=0
15-15*1/3=10
3-3*1=0
0-0*1/27=0
0-0*0=0
1-1*0=1
Вторая симплексная таблица
| Оценка базисных переменных | Базисные переменные | Свободные члены | 5 | 6 | 0 | 0 | 0 |
| С | Х | Р0 | Р1 | Р2 | Р3 | Р4 | Р5 |
| 6 | Х2 | 22 | 1/3 | 1 | 1/27 | 0 | 0 |
| 0 | Х4 | 472 | 10 | 0 | 0 | 1 | 0 |
| 0 | Х5 | 774 | 10 | 0 | 0 | 0 | 1 |
| С | 132 | -3 | 0 | -2/9 | 0 | 0 | |
Переход к новому опорному плану, выбор разрешающего столбца:
СК=мин{Сj(cj|<0)}=мин {-3; 0}=--3=С1=К=1
Выбор разрешающей строки:
bl/ alk=min {bi/ai1(ai1>0)}min{22/1/3;472/10;774/10}={66;47;77}=47=b2/a21=l=2
Генеральный элемент: alk=а21=10
Переход к новой симплексной таблице:
B2= b1/ а21=472/10=47
c=C-ckbс=c-c2b1=0-(-3)*47=148
alj=alj/alk
10/10=1
0/10=0
=0/10=0
=1/10
0/10=0
-3-(-3)*1=0
0-(-3)*0=0
2/9-(-3)*0=2/9
0-(-3)*1/10=0+3/10=3/10
0-(-3)*0=0
=6
=774-10*47=304
1/3-1/3=0
1-1*0=1
1/27-1/27*0=1/27
0-0*1/10=0
0-0*0=0
10-10*1=0
0-0*0=0
0-0*0=0
0-0*1/10=0
1-1*0=1
Третья симплексная таблица
| Оценка базисных переменных | Базисные переменные | Свободные члены | 5 | 6 | 0 | 0 | 0 |
| С | Х | Р0 | Р1 | Р2 | Р3 | Р4 | Р5 |
| 6 | Х2 | 6 | 0 | 1 | 1/27 | 0 | 0 |
| 5 | Х1 | 47 | 1 | 0 | 0 | 1/10 | 0 |
| 0 | Х5 | 304 | 0 | 0 | 0 | 0 | 1 |
| С | 148 | 0 | 0 | 2/9 | 3/10 | 0 | |
Проверка опорного плана на оптимальность:
СК=min{Сj(cj|<0)}=min (0;0;2/9;3/10;0)=0
Полученный план оптимален.
В векторном виде опорный план выглядит:
=(47;6;0;0;304)
С()=148
Экономическая интерпретация задачи:
Объём производства будет оптимальным при достижении максимальной прибыли-148 д.ед., и при объёме производства товара-6 шт. и 47 шт.
Похожие работы
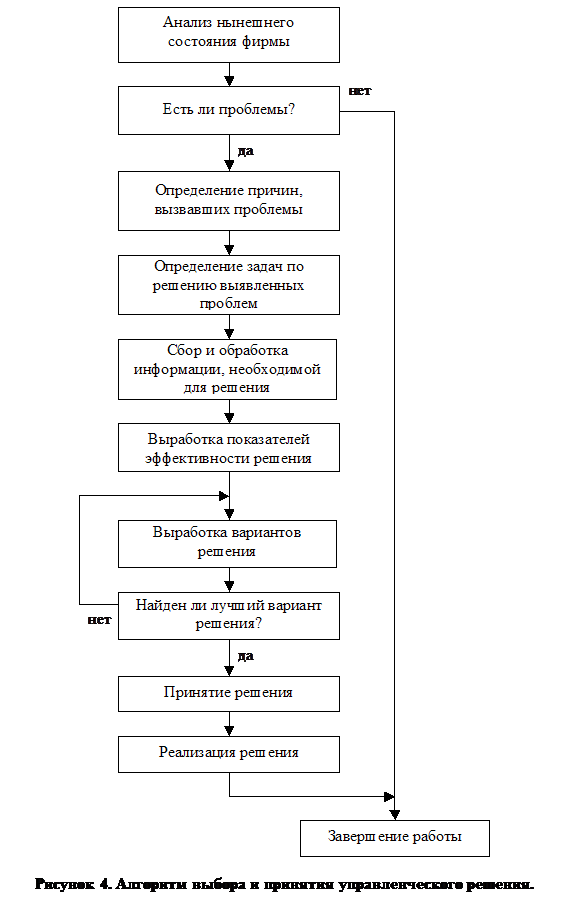
... элемента на качество принимаемых управленческих решений - одна из главных задач оптимизации процессов принятия решений в управлении общественным производством. Одним из условий преодоления субъективизма при подготовке управленческих решений являются методы исследования операций, методы экспертных оценок. Процедура выработки управленческих решений, являясь сложным логико-мыслительным процессом, ...
... , она измеряема количественными методами, она имеет сроки реализации, она согласовывается с глобальной целью деятельности всей организации. В практической части моей работы я рассмотрю процесс принятия управленческого решения по решению выявленной проблемы и устранению неудовлетворительных результатов работы. 3. Научно-методическая часть Управленческое решение – это фиксированный ...
... данный курс изучается студентами одним из последних, многие из перечисленных условий повышения качества и эффективности управленческих решений изучались ранее в других курсах и здесь они не будут рассматриваться. Например, вопросы правового, ресурсного обеспечения разработки и реализации управленческого решения, автоматизации процессов управления, компоненты внешней среды системы изучались в ...
... , если оно будет признано теми, кого оно затрагивает, установление обратной связи. 2. АНАЛИЗ И ОЦЕНКА ТЕХНОЛОГИЙ РАЗРАБОТКИ И ПРИНЯТИЯ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ В КУЛЬТУРНО-ОЗДОРОВИТЕЛЬНОМ КОМПЛЕКСЕ «ПОБЕДА» 2.1 Организационно-правовая характеристика комплекса Фирменное название предприятия – открытое акционерное общество «Курортно-оздоровительный комплекс «Победа». Юридическое место ...
0 комментариев