Оптимизационные модели принятия решений

  ТЕМА ОПТИМИЗАЦИОННЫЕ МОДЕЛИ ПРИНЯТИЯ РЕШЕНИЙ
ГЛАВА 1. Использование оптимизационных моделей при принятии решений

Успешность решения подавляющего большинства экономических задач зависит от наиболее эффективного способа использования ресурсов (денег, товаров, сырья, оборудования, рабочей силы и др.). Именно эффективностью использования, как правило, ограниченных, ресурсов определяется конечный результат деятельности любой экономической системы (фирмы, предприятия, отрасли).

Экономическая суть методов оптимизации заключается в том, что, исходя из наличия определенных ресурсов, выбирается такой способ их использования (распределения), при котором обеспечивается максимум (или минимум) интересующего ЛПР показателя.

Задачи нахождения значений параметров, обеспечивающих экстремум функции  при наличии ограничений, наложенных на аргументы (независимые переменные) , носят общее название задач математического программирования.

Трудности, возникающие при решении задач математического программирования, определяются, в частности:

·  видом функциональной зависимости критерия эффективности, называемого также целевой функцией, от независимых переменных;

·  размерностью задачи, то есть количеством независимых переменных;

·  видом и количеством ограничений, которым удовлетворяют независимые переменные.

Среди задач математического программирования самыми простыми и наиболее хорошо изученными являются так называемые задачи линейного программирования (линейной оптимизации). Для них характерно то, что целевая функция линейно зависит от , а также то, что ограничения, накладываемые на независимые переменные, имеют вид линейных равенств или неравенств относительно этих переменных.

Такие задачи часто встречаются на практике – например, при решении проблем, связанных с распределением ресурсов, планированием производства, организацией работы транспорта и т.д. Во многих случаях расходы и доходы линейно зависят от количества закупленных или утилизированных средств (например, суммарная стоимость партии товаров линейно зависит от количества закупленных единиц; оплата перевозок производится пропорционально весам перевозимых грузов и т.п.).

Задачи линейного программирования, естественно, не исчерпывают все возможные типы взаимосвязей экономических параметров. Более сложными для анализа и численного решения являются задачи нелинейного программирования (нелинейной оптимизации), характеризуемые нелинейной зависимостью целевой функции и (или) функций-ограничений от независимых переменных .

Отметим еще два типа задач математического программирования, имеющих широкую распространенность в практике принятия управленческих решений.

Динамическое программирование служит для выбора наилучшего плана выполнения многоэтапных действий. В общем виде постановка задачи динамического программирования сводится к следующему. Имеется некоторая управляемая операция (целенаправленное действие), распадающаяся (естественно или искусственно) на ряд шагов (этапов). На каждом этапе осуществляется распределение и перераспределение ресурсов (управление) с целью улучшения ее результата в целом. Задача динамического программирования – определить оптимальное управление на каждом шаге и, тем самым, оптимальное управление всей операцией в целом.

Следует отметить также задачи стохастического программирования. Особенность данного класса задач заключается в том, что ищется оптимальное решение в условиях неполной определенности, когда ряд параметров, входящих в целевую функцию и ограничения, представляют собой случайные величины.

Решение задач динамического и стохастического программирования, а также ряда других задач (например, параметрического программирования), выходит за рамки настоящего курса лекций.

Линейные модели оптимизации в управлении

Сначала рассмотрим задачи линейной оптимизации (или оптимизационные задачи линейного программирования), математические модели которых содержат лишь линейные зависимости от переменных.

Как уже отмечалось, оптимизация, включающая теорию и методы решения задач, в которых критерий оптимальности (целевая функция) линейно зависит от параметров задачи, является наиболее разработанным разделом информационных технологий оптимальных решений. Линейные модели широко используются в теории и практике принятия управленческих решений.

Современные информационные технологии оптимизации решений широкого класса практических задач включают их формулировку (построение математической модели), математические методы и компьютерные программы решения этих задач, а также методы экономико-математического анализа оптимальных решений.

Общая задача линейной оптимизации заключается в нахождении максимума (минимума) линейной целевой функции

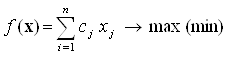, (2.1)

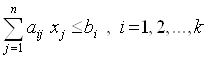, (2.2)

 , (2.3)

. (2.4)

Функция  называется целевой функцией, критерием оптимальности или линейной формой.

Вектор значений неизвестных , удовлетворяющих условию задачи (2.1)-(2.4), называется допустимым решением или допустимым планом задачи линейной оптимизации. Совокупность всех допустимых планов называется множеством допустимых планов. Допустимое решение  называется оптимальным, если оно обеспечивает максимальное (или, в зависимости от условий задачи, - минимальное) значение целевой функции.

Решение задач линейной оптимизации может быть получено без особых затруднений (естественно, при корректной формулировке проблемы). Классическим методом решения задач данного типа является симплекс-метод. В случае лишь двух переменных успешно может использоваться также графический метод решения, обладающий преимуществом наглядности. Очевидно, в случае  применение графического метода невозможно.

При решении ряда оптимизационных задач требуется, чтобы значения неизвестных выражались в целых числах. Естественно, к задачам подобного типа относятся те, в которых требуется определить необходимые для принятия решений значения физически цельных объектов (машин, агрегатов различного типа, людей, транспортных единиц и т.д. и т.п.). Такие задачи относятся к задачам целочисленной оптимизации. Математическая модель задачи линейной целочисленной оптимизации также определяется формулами (2.1)-(2.4), но в данном случае налагается дополнительное требование целочисленности всех (или части) неизвестных. Если требование целочисленности распространяется лишь на часть неизвестных величин задачи, то такая задача называется частично целочисленной.

Процесс построения математической модели для решения задачи начинается, как правило, с ответов на следующие вопросы:

·  Для определения каких величин должна быть построена модель, т.е. как идентифицировать переменные задачи?

·  Какие ограничения должны быть наложены на переменные, чтобы выполнялись условия, характерные для моделируемой системы?

·  В чем состоит цель задачи, для достижения которой из всех допустимых значений переменных нужно выбрать те, которые будут соответствовать оптимальному (наилучшему) решению задачи?

После ответа на данные вопросы для построения модели остается только идентифицировать переменные и представить цель и ограничения в виде математических функций этих переменных.

Надлежащий анализ вопросов подобного рода и корректная формулировка математической модели являются центральным звеном решения задач линейной (и не только линейной) оптимизации.

Эффективным средством решения задач линейной оптимизации является MS Excel. Входящий в состав данного программного продукта пакет Поиск решения (Solver) позволяет проводить решения задач подобного рода с большим (свыше 200) числом переменных и ограничений.

Отметим, что применительно к задачам оптимизации производственной программы предприятия наиболее типичными задачами линейной оптимизации являются оптимизация дохода, прибыли, себестоимости, номенклатуры производимой продукции, затрат станочного времени и т.п.

Рассмотрим использование информационных технологий решения задач линейной оптимизации на ряде конкретных примеров, имеющих непосредственное отношение к практике принятия управленческих решений.

Пример 1. Определение оптимального ассортимента продукции

Предприятие изготавливает два вида продукции П1 и П2 , которая поступает в оптовую продажу. Для производства используются два вида сырья  и . Максимально возможные запасы сырья в сутки составляют 9 и 13 единиц соответственно. Расход сырья на единицу продукции приведен в таблице.

Таблица 2.1

Сырье	Расход сырья на единицу продукции		Запас сырья, ед.
	П1	П2
	2	3	9
	3	2	13

Маркетинговые исследования показали, что суточный спрос на продукцию П1 не превышает спрос на продукцию П2 более чем на