Навигация
МЕТРОЛОГИЧЕСКИЕ СВОЙСТВА И МЕТРОЛОГИЧЕСКИЕ ХАРАТЕРИСТИКИ СРЕДСВ ИЗМЕРЕНИЙ
4. МЕТРОЛОГИЧЕСКИЕ СВОЙСТВА И МЕТРОЛОГИЧЕСКИЕ ХАРАТЕРИСТИКИ СРЕДСВ ИЗМЕРЕНИЙ
Метрологические свойства СИ — это свойства, влияющие на результат измерений и его погрешность. Показатели метрологических свойств являются их количественной характеристикой и называются метрологическими характеристиками.
Метрологические характеристики, устанавливаемые нормативным документом, называют нормируемыми метрологическими характеристиками.
Все метрологические свойства СИ можно разделить на две группы:
1) свойства, определяющие область применения СИ;
2) свойства, определяющие точность (правильность и прецизионность) результатов измерения.
К основным метрологическим характеристикам, определяющим свойства первой группы, относятся диапазон измерений и порог чувствительности.
Диапазон измерений — область значений величины, в пределах которых нормированы допускаемые пределы погрешности. Значения величины, ограничивающие диапазон измерений снизу или сверху (слева и справа), называют соответственно нижним или верхним пределом измерений.
Порог чувствительности — наименьшее изменение измеряемой величины, которое вызывает заметное изменение выходного сигнала. Например, если порог чувствительности весов равен 10 мг, то это означает, что заметное перемещение стрелки весов достигается при таком малом изменении массы, как 10 мг.
К метрологическим свойствам второй группы относя два главных свойства точности: правильность и прецизиность результатов.
К метрологическим характеристикам, определяю точность относятся погрешности СИ.
Погрешность средства измерений - это разность между показаниями СИ и действительным значением измеряемой величины. Поскольку истинное значение физической величины неизвестно, то на практике пользуются ее действительным значением. Для рабочего СИ за действительное значение принимают показания рабочего эталона низшего разряда (допустим, 4-го), для эталона 4-го разряда, в свою очередь, — значение величины, полученное с помощью рабочего эталона 3-го разряда. Таким образом, за базу для сравнения принимают значение СИ, которое является в поверочной схеме вышестоящим по отношению к подчиненному СИ, подлежащему поверке:
∆Хп = Хп - Х0 (3)
где ∆Хп — погрешность поверяемого СИ; Хп — значение той же самой величины, найденное с помощью поверяемого СИ; Х0 — значение СИ, принятое за базу для сравнения, т.е. действительное значение.
Погрешности СИ могут быть классифицированы по ряду признаков, в частности:
· по способу выражения — абсолютные, относительные;
· по характеру проявления — систематические, случайные;
· по отношению к условиям применения — основные, дополнительные.
Наибольшее распространение получили метрологические свойства, связанные с первой группировкой — с абсолютными и относительными погрешностями. Определяемая по формуле (3) ∆Хп является абсолютной погрешностью. Однако в большей степени точность СИ характеризует относительная погрешность (δ), т.е. выраженное в процентах отношение абсолютной погрешности к действительному значению величины, измеряемой или воспроизводимой данным СИ:
δ =100*∆Хп/Хо
Точность может быть выражена обратной величиной относительной погрешности — 1/ δ. Если погрешность δ = 0,1%, или 0,001=10-3, то точность равна 103.
В стандартах нормируют характеристики, связанные с другими погрешностями.
Систематическая погрешность — составляющая погрешности результата измерения, остающаяся постоянной (или же закономерно изменяющейся) при повторных измерениях одной и той же величины. Ее примером может быть погрешность градуировки, в частности погрешность показаний прибора с круговой шкалой и стрелкой, если ось последней смещена на некоторую величину относительно центра шкалы. Если эта погрешность известна, то ее исключают из результатов разными способами, в частности введением поправок. При химическом анализе систематическая погрешность проявляется в случаях, когда метод измерений не позволяет полностью выделить элемент или когда наличие одного элемента мешает определению другого.
При нормировании систематической составляющей погрешности СИ устанавливают пределы допускаемой систематической погрешности СИ конкретного типа — D.
Величина систематической погрешности определяет такое метрологическое свойство, как правильность измерений СИ, — это первая составляющая точности.
Случайная погрешность — составляющая погрешности результата измерения, изменяющаяся случайным образом (по знаку и значению) в серии повторных измерений одного и того же размера величины с одинаковой тщательностью. В появлении этого вида погрешности не наблюдается и какой-либо закономерности. Они неизбежны и неустранимы, всегда присутствуют в результатах измерения. При многократном и достаточно точном измерении они порождают рассеяние результатов.
Характеристиками рассеяния являются средняя арифметическая погрешность, средняя квадратическая погрешность, размах результатов измерений. Поскольку рассеяние носит вероятностный характер, то при указании на значения случайной погрешности задают вероятность.
Величина случайной погрешности определяет вторую составляющую точности – прецизионность.
Оценка погрешности измерений СИ, используемых для определения показателей качества товаров, определяется спецификой применения последних. Например, погрешность измерения цветового тона керамических плиток для внутренней отделки жилища должна быть по крайней мере на порядок ниже, чем погрешность измерения аналогичного показателя серийно выпускаемых картин, сделанных цветной фотопечатью. Дело в том, что разнотонность двух наклеенных рядом на стену кафельных плиток будет бросаться в глаза, тогда как разнотонность отдельных экземпляров одной картины заметно не проявится, так как они используются разрозненно.
Номенклатура нормируемых метрологических характеристик СИ определяется назначением, условиями эксплуатации многими другими факторами. У СИ, применяемых высокоточных измерений, нормируется до десятка и болee метрологических характеристик в стандартах технических требований (технических условий) и ТУ. Нормы на ровные метрологические характеристики приводятся в эксплуатационной документации на СИ. Учет всех нормируемых характеристик необходим при измерениях высокой точности и в метрологической практике. В повседневной производственной практике широко пользуются обобщенной характеристикой — классом точности.
Класс точности СИ — обобщенная характеристика, выражаемая пределами допускаемых (основной и дополнительной) погрешностей, а также другими характеристиками влияющими на точность. Классы точности конкретного типа СИ устанавливают в НД. При этом для каждого класса точности устанавливают конкретные требования к метрологическим характеристикам, в совокупности отражающим уровень точности СИ данного класса.
Класс точности позволяет судить о том, в каких пределах находится погрешность измерений этого класса.
Похожие работы
... их значений от типовых сделать выводы о неполадках в ЭСУ и в двигателе. 3.1.3. Сканер CARMAN SCAN VG. CARMAN SCAN VG это интегрированная информационная система, которая позволяет проводить диагностику автомобилей ведущих мировых производителей в режиме реального времени. Система также имеет функцию записи сигнала и самодиагностики. Перед началом работы со сканером CARMAN SCAN VG необходимо ...
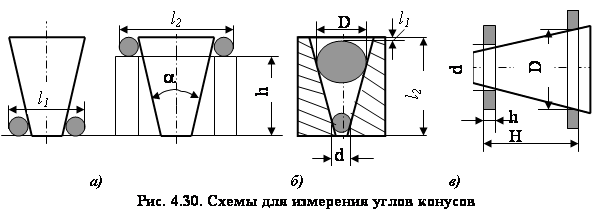
... угла от эталонов к образцовым и рабочим угловым мерам, поверки и градуировки угломерных приборов и специальных угловых мер (шаблонов), а также для непосредственного измерения угловых изделий. По ГОСТу 2875 - 88 "Меры плоского угла призматические. Общие технические условия" предусмотрено пять типов угловых мер (рис. 4.20): меры типа 1 выполнены со срезанной вершиной угла и имеют малые (до 9о) ...
... с ценой деления 1 сек. Области применения: построение геодезических сетей сгущения (триангуляция 4 класса, полигонометрия IV класса), в прикладной геодезии (строительство, изыскания и т.д.), астрономо- геодезических измерениях (определение азимута по Солнцу и по Полярной Звезде). Модель 3Т5КП предназначена для измерения горизонтальных и вертикальных углов и не имеет микрометра. Области ...
... причин возникновения погрешностей и уменьшение размеров погрешностей — одна из главных задач практической метрологии, поэтому понятие «погрешность» — одно из центральных в метрологии. 2. Классификация погрешностей измерений 2.1. По форме представления погрешности разделяются на абсолютные, относительные и приведённые. Абсолютная погрешность ∆ измерений, выражаемея в единицах ...

0 комментариев