Навигация
Найти нормированные значения коэффициентов нижних частот B и С из соответствующей таблицы в приложении А
1. Найти нормированные значения коэффициентов нижних частот B и С из соответствующей таблицы в приложении А.
2. Выбрать номинальное значение емкости C1 (предпочтительно близкое к значению 10/fc мкФ) и вычислить значения сопротивлений по (20).
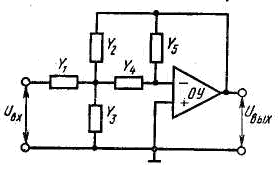
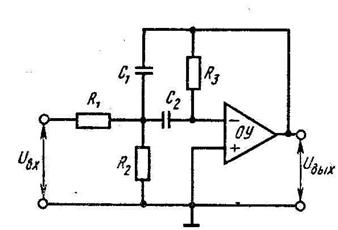
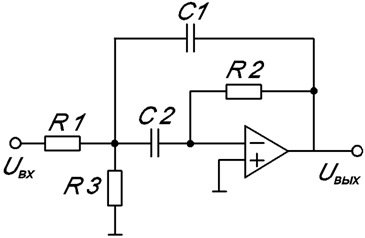
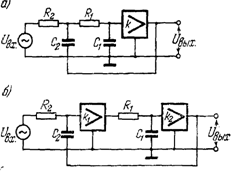
3. Выбрать номинальные значения, наиболее близкие к вычисленным значениям, и реализовать фильтр или его звенья в соответствии со схемой, показанной на рис. 8.
Комментарии
а. Сопротивления R3 и R4 обеспечивают К>1 и выбираются таким образом, чтобы минимизировать смещение ОУ по постоянному току.
Коэффициент звена неинвертирующий и равен
K=l+(R4/R3),
поэтому можно использовать другие значения сопротивлений R3 и R4 при условии сохранения их отношения. Если требуется получить K=1, то сопротивление R3 заменяется на разомкнутую, а сопротивление R4 на короткозамкнутую цепи, и в этом случае эта схема работает на повторителе напряжения.
б. Изменяя сопротивления R1 и R2 в равном процентном отношении, можно установить частоту среза fc без воздействия на добротность Q. Коэффициент усиления К можно установить, используя вместо резисторов R3 и R4 потенциометр, центральный отвод которого соединяется с инвертирующим входом ОУ.
4. ПОЛОСОВЫЕ ФИЛЬТРЫ 4.1 ОБЩИЙ СЛУЧАЙ
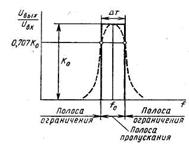
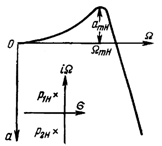
Полосовой фильтр представляет собой устройство, которое пропускает сигналы в диапазоне частот с шириной полосы BW, расположенной приблизительно вокруг центральной частоты fo (Гц) или wo=2πfo (рад/с). На рис. 9 изображены идеальная и реальная амплитудно-частотные характеристики. В реальной характеристике частоты wL и wU представляют собой нижнюю и верхнюю частоты среза и определяют полосу пропускания wL≤w≤wU и ее ширину BW=wU.- wL

Рис. 9. Идеальная и реальная амплитудно-частотные характеристики полосового фильтра.
В полосе пропускания амплитудно-частотная характеристика никогда не превышает некоторого определенного значения, например А1 на рис. 9. Существует также две полосы задерживания 0≤w≤w1 и w≥w2, где значение амплитудно-частотной характеристики никогда не превышает заранее выбранного значения, скажем A2. Диапазоны частот между полосами задерживания и полосой пропускания, а именно w1<w<wL и wU<w<w2, образуют соответственно нижнюю и верхнюю переходные области, в которых характеристика является монотонной.
Передаточные функции полосовых фильтров можно получить из нормированных функций нижних частот переменной s с помощью преобразования
 (21)
(21)
Отношение Q=wo/BW характеризует качество самого фильтра и является мерой его избирательности. Высокому значению Q соответствует относительно узкая, а низкому значению Q — относительно широкая ширина полосы пропускания. Коэффициент усиления фильтра К определяется как значение его амплитудно-частотной характеристики на центральной частоте; таким образом K=│H(jwo)│.
В каждом случае центральная частота и частота среза связаны следующим соотношением:
![]() ,
,
где
 (22)
(22)
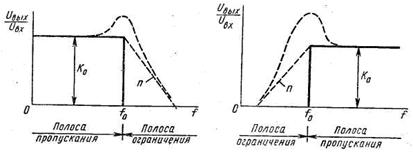
Путем последовательного соединения ФНЧ и ФВЧ получаются полосовые фильтры с широкой полосой пропускания. При этом частота среза фильтра нижних частот должна быть выше частоты среза верхних частот и лишь в частном случае эти частоты могут быть взяты равными.
5. РАСЧЕТНАЯ ЧАСТЬ.
Исходные данные для курсовой работы:
порядок фильтра – 4
граничные частоты фильтра – 100Гц, 18кГц;
коэффициент передачи по напряжению – 1;Анализируя рассмотренный материал, делаем вывод, что наиболее подходящим в нашем случае будет использование фильтра Баттерворта, реализованного схемой на ИНУН.
Полосовой фильтр четвертого порядка можно реализовать, соединив каскадно два НЧ и два ВЧ фильтра вторых порядков (п. 4.1).

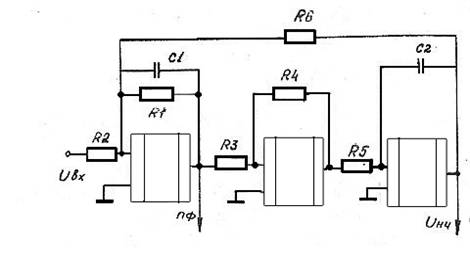
Рис. 10. Активный полосовой фильтр 4-го порядка.
Рассчитаем в отдельности НЧ и ВЧ фильтры, используя методику, рассмотренную в п.2.4 и 3.3.
5.1 РАСЧЕТ ФНЧ ЧЕТВЕРТОГО ПОРЯДКАФильтр получен путем каскадного включения двух ФНЧ второго порядка.
Расчет ведется в соответствии с п. 2.4. Коэффициенты звена второго порядка фильтра Баттерворта берутся из приложения A [1]. Для звена второго порядка В=1,1 и С=1,1. По условию курсовой работы К=1 и fc=18000 Гц.
Расчет звена второго порядка:
· Значение емкости С1 выбирается близким к значению 10/fc мкФ.
10/fc мкФ=10/18000 мкФ=0,55 нФ.
Выберем значение С1=0,6нФ.
С2 выбирается из условия
 .
.

Получаем условие С2£0,165 нФ. Выбираем С2=0,16 нФ.
R1 находим по формуле

R1=21,4 кОм.
R2 находим по формуле

R2=34,6 кОм.
Значения элементов C3, C4, R3 и R4 выбираем следующими:
C3=C1=0,6нФ, C4=C2=0,16 нФ, R3=R1=21,4 кОм, R4=R2=34,6 кОм.
5.2 РАСЧЕТ ФВЧ ЧЕТВЕРТОГО ПОРЯДКАФильтр получен путем каскадного включения двух ФВЧ второго порядка.
Расчет ведется в соответствии с п. 3.3. Коэффициенты звена второго порядка фильтра Баттерворта берутся из приложения А [1]. Для звена второго порядка В=1,1 и С=1,1. По условию курсовой работы К=1 и fc=100 Гц.
Расчет звена второго порядка:
Емкость С5=C6 выбирается произвольно. Пусть С5=C6=100 нФ.
R6 находим по формуле:

R6=31,8 кОм
R5 находим по формуле:

R5=8,76 к Ом.
Значения элементов C7, C8, R7 и R8 выбираем следующими:
C7=C8=C5=C6=100 нФ, R7=R5=8,76 кОм, R8=R6=31,8 кОм.
5.3 ВЫБОР ЭЛЕМЕНТОВОУ выбираем из условий, что его коэффициент усиления должен быть больше коэффициента усиления фильтра минимум в 50 раз и частота среза ОУ была значительно больше частот среза фильтра.
Исходя из этих соображений выбираем ОУ К574УД1А со следующими характеристиками:
напряжение питания ±15 В;
потребляемый ток 8 мА;
минимальный коэффициент усиления 5e+04;
напряжение смещения 50 мВ;
входной ток 0,5 нА;
входное сопротивление 10 ГОм;
граничная полоса частот 10 МГц.
Выбор резисторов и конденсаторов:
Поскольку в нашем случае достаточно применять элементы с 5%−ным допуском, резисторы и конденсаторы выбираем из ряда Е24, который включает в себя следующие значения:
| 1,0 | 1,5 | 2,2 | 3,3 | 4,7 | 6,8 |
| 1,1 | 1,6 | 2,4 | 3,6 | 5,1 | 7,5 |
| 1,2 | 1,8 | 2,7 | 3,9 | 5,6 | 8,2 |
| 1,3 | 2,0 | 3,0 | 4,3 | 6,2 | 9,1 |
Для построения схемы будем использовать металлодиэлектрические резисторы Р1−4, для которых диапазон значений сопротивлений – 10…106 Ом. Максимальную рассеиваемую мощность резисторов определяем из условия Рн>I2R, где I − входной ток ОУ, R − номинальное сопротивление резистора. Для всех резисторов, входящих в схему, это условие выполняется для Рн=0,25 Вт.
В соответствии с таблицей и рассчитанными значениями сопротивлений получаем:
| R1=21,4 кОм | P1−4−0,25−22кОм±5% |
| R2=34,6 кОм | P1−4−0,25−36кОм±5% |
| R3=21,4 кОм | P1−4−0,25−22кОм±5% |
| R4=34,6 кОм | P1−4−0,25−36кОм±5% |
| R5=8,76 кОм | P1−4−0,25−9,1кОм±5% |
| R6=31,8 кОм | P1−4−0,25−33кОм±5% |
| R7=8,76 кОм | P1−4−0,25−9,1кОм±5% |
| R8=31,8 кОм | P1−4−0,25−33кОм±5% |
Конденсаторы выберем типа К10−17 и К10-17-1, для которых диапазон значений емкостей составляет 910пФ-1,5мкФ и 2,2пФ-22000пФ соответсвенно:
| С1=0,6 нф | К10−17−25В−620пФ±5% |
| С2=0,16 нФ | К10−17−1-40В−160пФ±5% |
| С3=6 нФ | К10−17−25В−620пФ±5% |
| С4=0,16 нФ | К10−17−1–40В−160пФ±5% |
| С5=100 нФ | К10−17−25В−100нФ±5% |
| С6=100 нФ | К10−17−25В−100нФ±5% |
| С7=100 нФ | К10−17−25В−100нФ±5% |
| С8=100 нФ | К10−17−25В−100нФ±5% |
Спецификация по приведенным выше элементам представлена отдельным файлом Specification.doc.
5.4 АНАЛИЗ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ
Схема была построена и проанализирована в программе Electronic Workbench.
1. Проведем исследование схемы, используя в качестве номиналов пассивных элементов значения, полученные при рассчетах, а в качестве ОУ – идеальную его модель.

Рис. 11. Схема испытаний.
На рис.12 представлены АЧХ данного полосового фильтра:


Рис. 12. АЧХ полосового фильтра.
Проведем исследование схемы, используя в качестве номиналов пассивных элементов значения, указанные в спецификации (в соответствии с ГОСТ), с разбросом 5%, а в качестве ОУ – модель выбранной микросхемы К574УД1А.

Рис. 13. Схема испытаний.
На рис.14 представлены АЧХ данного полосового фильтра:


Рис. 14. АЧХ полосового фильтра.
ЗАКЛЮЧЕНИЕ.
В ходе работы был рассчитан полосовой фильтр с широкой полосой пропускания и максимально плоской АЧХ в полосе пропускания со следующими характеристиками:
порядок фильтра – 4;
граничные частоты фильтра 100Гц, 18кГц;
коэффициент передачи по напряжению в полосе пропускания – 1.Фильтр построен на следующих элементах: К574УД1А, К10−17, К10-17-1, Р1−4.
Фильтр построен на элементах с 5%−ным разбросом технологических параметров. Рассчитанные номинальные значения пассивных элементов следующие:
| Резисторы | Конденсаторы |
| R1=21,4 кОм | С1=6 нф |
| R2=34,6 кОм | С2=0,16 нФ |
| R3=21,4 кОм | С3=6 нФ |
| R4=34,6 кОм | С4=0,16 нФ |
| R5=8,76 кОм | С5=100 нФ |
| R6=31,8 кОм | С6=100 нФ |
| R7=8,76 кОм | С7=100 нФ |
| R8=31,8 кОм | С8=100 нФ |
Фильтр может использоваться для усиления или ослабления определенных частот, в генераторах электромузыкальных инструментов, в сейсмических приборах, в линиях связи, для изучения частотного состава сигналов.
ПЕРЕЧЕНЬ ИСПЛЬЗУЕМЫХ ИСТОЧНИКОВ.
1. Справочник по активным фильтрам: Пер. с англ./Д. Джонсон, Дж. Джонсон, Г. Мур. − М.: Энергоатомиздат, 1983.
2. Гусев В.Г., Гусев Ю.М. Электроника. М.: Высшая школа, 1991.
3. Быстров Ю.А., Мироненко И.Г. Электронные цепи и устройства. М.: Высшая школа, 1989.
4. Гутников В.С. Интегральная электроника в измерительных устройствах. Л.: Энергия, 1980.
5. Разработка и оформление конструкторской документации РЭА: Справ. пособие/ Э.Т. Романычева, А.К. Иванов и др. М.: Радио и связь. 1984.
6. Резисторы, конденсаторы, трансформаторы, дроссели, коммутационные устройства РЭА: Справ./ Н.Н. Акимов, Е.П. Ващуков, В.А. Прохоренко, Ю.П. Ходоренок. Мн.: Беларусь, 1994.
7. Радиоэлектронные устройства: Справ./ Б.И. Горошков. М.: Радио и связь, 1984.
8. www.rlocman.ru.
9. www.gaw.ru.
10. www.nnov.rfnet.ru.
11. www.promelec.ru.
Похожие работы
... со строго постоянным коэффициентом передачи в полосе пропускания, бесконечным ослаблением в полосе подавления и бесконечной крутизной спада при переходе от полосы пропускания к полосе подавления. Проектирование активного фильтра всегда представляет собой поиск компромисса между идеальной формой характеристики и сложностью ее реализации. Это называется "проблемой аппроксимации". Во многих случаях ...
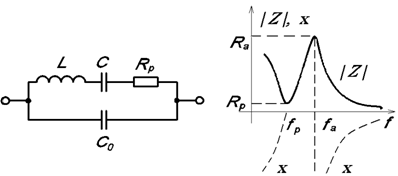
... , достигая сопротивления Rp – активного сопротивления, отображающего наличие потерь при колебаниях пластины резонатора. Рис.3 Активные фильтры Принцип действия фильтров RC. Устройства фильтрации, в которых используются контуры LC, по принципу действия являются пассивными, т.е. предполагается, что для их функционирования не требуется усилительных активных элементов. Усиление производится ...
... n = 2. По таблицам приложения определяем полюсы низкочастотной аппроксимирующей функции и количество активных резонаторов. Количество резонаторов – 4. Рассчитаем добротность полосового фильтра Вычислим параметры y и r и добротность активных резонаторов. Где Re и Im – действительная и мнимая части полюсов резонаторов. Вычислим добротность резонаторов Определим ...
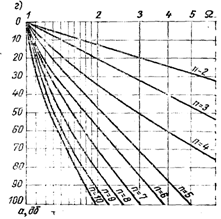
... целесообразно решать аппроксимационную задачу. Определим нормированную частоту ограничения фильтра, как отношение = = 0,6666. Нормированная частота в полосе задерживания обычного фильтра НЧ равна . Эта же частота в случае фильтра НЧ с ограниченной полосой пропускания рассчитывается по формуле Из кривых (рис. 1.) по вычисленной и заданным и а определим ...
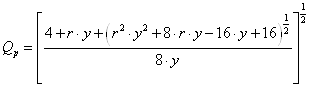

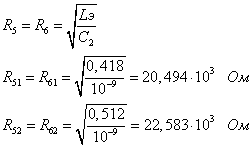
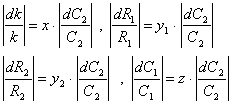
0 комментариев