Навигация
1.4 ПОСЛЕДОВАТЕЛЬНОСТИ
Массивы - это гибкая структура данных. Размер массива может быть очень велик и не умещаться в памяти компьютера, в этих случаях данные хранятся на магнитных носителях. Такие массивы размеры, которых очень велики, принято называть последовательностями. Последовательностный тип можно было бы описать следующим образом:
TYPE T = SEQUENCE OF To
Уже из описания ясно, что все элементы последовательности имеют один и тот же тип. Последовательность s из п элементов мы будем обозначать s = <s0, s1,s2, ..., sn-1>, причем N называется длиной последовательности. Прямое следствие бесконечности мощности последовательностного типа — невозможность выделить для соответствующей переменной память заданного размера. Вместо этого мы должны выделять память в процессе выполнения программы по мере роста последовательности. Если же последовательность уменьшается, то память можно и возвращать. В любом случае следует пользоваться некой схемой динамического распределения. Последовательности по существу присутствуют во всех приложениях вычислительных машин, они как бы вездесущи. Данные такой структуры превалируют во всех тех случаях, когда идет работа с памятями разного вида, т. е. когда данные передаются из внешней памяти, скажем дисков или лент, в оперативную, главную память и обратно.
Преимущество такой приверженности последовательному доступу, который, как бы то ни было, представляет собой серьезное ограничение, заключается в относительной простоте требуемого механизма управления памятью. Но еще более важной, если речь идет об обменах данными со вторичной памятью, выглядит возможность пользоваться эффективной техникой буферизации. Последовательный доступ позволяет нам для «перекачки» данных между памятями различного вида использовать непрерывные потоки данных. Буферизация предполагает, что части потока накапливаются в так называемых буферах, а затем, уже при заполнении всего буфера, передаются куда нужно. В результате, что особенно важно, более эффективно используется вторичная память.
Нижеприведенная часть программы показывает как обычно реализуется последовательность
DEFINITION MODULE FileSystem;
FROM SYSTEM IMPORT WORD;
CONST MaxLength = 4096:
TYPE Sequence = RECORD pos, length: CARDINAL;
eof: BOOLEAN;
a: ARRAY [0 „ Maхength-1 OF WORD
END;
PROCEDURE Open(VARf; Sequence):
PROCEDURE WriteWord(VAR f: Sequence; w; WORD)!
PROCEDURE Reset(VAR f:Sequence);
PROCEDURE ReadWord(VAR f: Sequence; VAR W; WORD);
PROCEDURE Close(VAR f: Sequence);
END FileSystem.
Обратите внимание, что в этом примере максимальная достижимая длина последовательности — произвольная константа. Если в какой-либо программе случится, что последовательность станет длиннее, то это будет рассматриваться не как ошибка в программе, а скорее как неадекватная реализация. С другой стороны, операция чтения за фактическим текущим концом последовательности действительно должна считаться ошибкой в программе.
1.5 СОРТИРОВКА ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Прямое слияние
К сожалению, алгоритмы сортировки, приведенные в предыдущем разделе, невозможно применять для данных, которые из-за своего размера не помещаются в оперативной памяти машины и находятся, например, на внешних, последовательных запоминающих устройствах памяти, таких, как ленты или диски.
В таком случае мы говорим, что данные представляют собой (последовательный) файл.. Наиболее важный из них — сортировка с помощью слияния. Слияние означает объединение двух (или более) последовательностей в одну-единственную упорядоченную последовательность с помощью повторяющегося выбора из доступных в данный момент элементов. Слияние намного проще сортировки, и его используют как вспомогательную операцию в более сложных процессах сортировки последовательностей. Одна из сортировок на основе слияния называется простым, слиянием. Она выполняется следующим образом:
1. Последовательность а разбивается на две половины: b и с.
2. Части b и с сливаются, при этом одиночные элементы образуют упорядоченные пары.
3. Полученная последовательность под именем о вновь обрабатывается как указано в пунктах 1, 2;при этом упорядоченные пары переходят в такие же четверки.
4. Повторяя предыдущие шаги, сливаем четверки в восьмерки и т. д., каждый раз «удваивая» длинуслитых подпоследовательностей до тех пор, пока не будет упорядочена целиком вся последовательность.
Действия по однократной обработке всего множества данных называются фазой. Наименьший же подпроцесс, повторение которого составляет процесс сортировки, называется проходом или этапом.
Теперь перейдем к более детальному рассмотрению программы слияния. Данные мы будем представлять как массив, обращение к элементам которого, однако, идет строго последовательно. Если рассматривать массив как последовательность элементов, имеющих два конца, то его весьма просто можно использовать вместо двух последовательностей. Мы будем при слиянии брать элементы с двух концов массива, а не из двух входных файлов.Направление пересылки сливаемых элементов изменяется на первом проходе после каждой упорядоченной пары, на втором — после каждой упорядоченной четверки и т. д., равномерно заполняя две выходные последовательности, представляемые двумя концами одного массива. После каждого прохода массивы «меняются ролями», выходной становится входным и наоборот.
Если объединить два концептуально различных массива в один-единственный, но двойного размера, то программа еще более упрощается. В этом случае данные представляются так:
a: ARRAY[1..2*n] OF item
Начальное значение р равно 1, и перед каждым последующим проходом она удваивается. Для простоты мы предполагаем, что всегда n равно степени двойки. Таким образом, первая версия программы сортировки с помощью простого слияния имеет такой вид
PROCEDURE MergeSort:
VAR i, j, k, L: index; up: BOOLEAN; p: INTEGER;
BEGIN up : = TRUE; p : = 1;
REPEAT инициации индексов;
IFupTHEN i:=l; j:=n; k:=n+1;L:=2*n
ELSE k:= l;L:= n; i := n+1; j := 2*n
END;
слияние р-наборов из i- и j-входов в k- и L-выходы;
Up:= ~up; p:=2*p
UNTIL p = n
END MergeSort
Следующий этап — уточнение операторов, выделенных курсивом. Ясно, что процесс слияния n элементов сам представляет собой последовательность слияний последовательностей, т. е. р-наборов. После каждого такого частичного слияния выход переключается с нижнего на верхний конец выходного массива и наоборот, что гарантирует одинаковое распределение в обоих направлениях. Если сливаемые элементы направляются в левый конец выходного массива, то направление задается индексом к и после пересылки очередного элемента он увеличивается на единицу. Если же элементы направляются в правый конец, то направление задается индексом L и он каждый раз уменьшается. Для упрощения фактического оператора слияния будем считать, что направление всегда задается индексом к, но после слияния р-набора будем менять местами значения к и L, приращение же всегда обозначается через h, имеющее значение либо 1, либо —1.
Поскольку на каждом проходе р удваивается и сортировка заканчивается при р> n, то всего требуется [logn] проходов. На каждом проходе по определению копируются по одному разу все n элементов
Алгоритм сортировки слиянием выдерживает сравнение даже с усовершенствованными методами. Однако, хотя здесь относительно высоки затраты на работу с индексами, решающее значение играет необходимость работать с памятью размером 2n. Поэтому сортировка слиянием для массивов, т. е. для данных, размещаемых в оперативной памяти, используется редко.
Естественное слияние
В случае прямого слияния мы не получаем никакого преимущества, если данные в начале уже частично упорядочены. Размер сливаемых на к-м проходе подпоследовательностей меньше или равен 2к и не зависит от существования более длинных уже упорядоченных подпоследовательностей, которые можно было бы просто объединить. Фактически любые две упорядоченные подпоследовательности длиной m иn можно сразу сливать в одну последовательность из m + n элементов. Сортировка, при которой всегда сливаются две самые длинные из возможных подпоследовательностей, называется естественным слиянием.
Упорядоченные подпоследовательности часто называют строками. Однако так как слово «строка» еще чаще употребляется для названия последовательности символов, то мы для упорядоченных подпоследовательностей будем использовать термин «серия». Поэтому в сортировке естественным слиянием объединяются (максимальные) серии, а не последовательности фиксированной (заранее) длины. Если сливаются две последовательности, каждая из n серий, то результирующая содержит опять ровно n серий. Следовательно, при каждом проходе общее число серии уменьшается вдвое и общее число пересылок в самом плохом случае равно n*|logn|, а в среднем даже меньше. Ожидаемое же число сравнений, однако, значительно больше, поскольку кроме сравнений, необходимых для отбора элементов при слиянии, нужны еще дополнительные — между последовательными элементами каждого файла, чтобы определить конец серии.
Следующим нашим упражнением будет создание алгоритма естественного слияния с помощью того же приема пошагового уточнения, который применялся при объяснении алгоритма прямого слияния.
VARL: INTEGER; а, b, с: Sequence
REPEAT Reset(a); Reset(b); Reset(c):
Распределение; (*с распределяется в а и b*)
Reset(a); Reset(b); Reset(c);
L: = 0; слияние (*а и b сливаются в с *)
UNTILL = 1
Две фазы явно выделяются как два различных оператора. Теперь их надо уточнить, т. е. переписать с большей детализацией. Уточненное описание распределения (distribute) приведены ниже .
RЕРЕАТ copyrun(c, a);
IF~c.eof THENcopyrun(c,b)END
UNTIL с.eof
REPEAT mergerun; L: = L+1
UNTIL b.eof;
IF ~a.eof THEN copyrun(a, c); L := L+l END
Такой метод распределения приводит предположительно к следующему результату: либо в а и b будет поровну серий, либо в а будет на одну больше. Поскольку соответствующие пары серий сливаются в одну, то b а может оказаться еще одна лишняя серия, ее нужно просто скопировать.
Вместо того чтобы программировать явно этот механизм в нашей программе, мы предпочитаем определить еще один уровень абстракции. Это будет новый модуль с именем Sequences, для пользователя он заменит модуль FileSystem. Кроме того, мы определяем соответственно и новый тип для последовательности, но он будет ссылаться на Sequence из FileSystem. В этом новом типе будет фиксироваться не только конец последовательности, но и конец серии и, конечно же, первый элемент оставшейся части последовательности. Новый тип и связанные с ним операции задаются таким модулем определений:
DEFINITION MODULE Sequences;
IMPORT FileSystem;
TYPE item = INTEGER;
Sequence = RECORD first: item;
eor.eof: BOOLEAN;
f: FileSystem.Sequence
END;
PROCEDURE OpenSeq(VARs: Sequence);
PROCEDURE OpenRandomSeq(VARs: Sequence; length, seed: INTEGER); PROCEDURE StartRead(VARs: Sequence);
PROCEDURE StartWrite(VAR s: Sequence);
PROCEDURE copy(VAR x, y: Sequence);
PROCEDURE CloseSeq(VAR s: Sequence);
PROCEDURE ListSeq(VAR s: Sequence);
END Sequences.
Процесс сравнения и выбора ключей при слиянии серий заканчивается, как только исчерпается одна из двух серий. После этого оставшаяся неисчерпанной серия просто передается в результирующую серию, точнее копируется ее «хвост».
Сбалансированное многопутевое слияние
Затраты на любую последовательную сортировку пропорциональны числу требуемых проходов, так как по определению при каждом из проходов копируются все данные. Один из способов сократить это число — распределять серии в более чем две последовательности. Слияние r серий поровну распределенных в N последовательностей даст в результате r/N серий. Второй проход уменьшит это число до г/N2, третий — до r/N3 и т. д., после к проходов останется r/Nkсерий. Поэтому общее число проходов, необходимых для сортировки n элементов с помощью N-путевого слияния, равно
k = [logNn]
В программе сортируется массив файлов. Мы начнем с определений и к двум уже знакомым типам item и sequence добавим тип
seqno = [l..N]
Теперь можно представить алгоритм.
MODULE BalancedMerge;
VAR1, j: seqno;
L: INTEGER; (* число распределяемых серий *).
t: ARRAY seqno OF seqno;
BEGIN (* распределение начальных серий в- t[l] ...t[Nh] *)
j:=Nh;L:=0;
REPEAT
IF j < Nh THEN x := j+l ELSE j: = 1 END;
копирование одной серии из f0 в последовательность J;
L:=L+1
UNTIL fo.eof;
FORi:=l TO N DO t[i]:=I END;
REPEAT (* слияние из t[l]...t[nh] в t[nh+l]...i[n]*)
установка входных последовательностей;
L: = 0;
j:=Nh+l; (*j -индекс выходной последовательности*)
REPEAT L:=L+1;
слияние а серий с входов b i(j);
IF j < N THEN j : = j+l ELSE j := Nh+I END
UNTIL все входы исчерпаны
переключение последовательностей
UNT1L L = 1
(• отсортированная последовательность в t [1 ] *)
END BalancedMerge,
Многофазная сортировка
Мы уже познакомились с необходимыми приемами и в достаточной мере готовы к исследованиям и программированию, связанным с новыми, более эффективными, чем сбалансированная сортировка, алгоритмами. В основе нашего очередного усовершенствования лежит отказ от жесткого понятия прохода и переход к более изощренному использованию последовательностей. Мы больше не будем считать, что есть N/2 входов и столько же выходов и они меняются местами после каждого отдельного прохода. Более того, уже само понятие прохода делается расплывчатым. Новый метод был изобретен Р. Гилстэдом [2.3] и называется многофазной сортировкой (Polyphase Sort).
Многофазная сортировка более эффективна, чем сбалансированная, поскольку она имеет дело с N—1-путевым слиянием, а не с N/2-путевым, если она начинается с N последовательностей. Ведь число необходимых проходов приблизительно равно logN *n, где n — число сортируемых элементов, а N — степень операции слияния, — это и определяет значительное преимущество нового метода.
Фактически операция слияния почти идентична той же операции в сортировке с помощью N-путевого слияния, разница только в том, что здесь алгоритм исключения последовательности несколько проще.
Глава 2. Практические задачи по алгоритмам обработки данных
Похожие работы
... конкретные примеры, наглядно это обосновывая. Для написания программ необходимо использовать особенные языки. Языки программирования - это нормированные языки, которые служат для описания инструкций обработки, структур данных, а также ввода и вывода данных. Необходимо преобразовывать алгоритм всегда таким образом, чтобы выделять в нем "подалгоритмы". Теория разработки программного обеспечения ...
... что мы не будем разграничивать понятия автоматизированной системы обработки документов и автоматизированной системы управления документооборотом, поскольку в современных информационных средах их функции часто объединены. Типовая компьютерная среда включает следующие основные компоненты: средства разработки сообщений; корпоративную информационную систему; систему документооборота и обработки ...
... и исправления ошибок в текстах на естественных языках (назовем их автокорректорами - АК, хотя терминология ещё не сложилась) получают все большее распространение. Они используются, в частности, в пакетах WINWORD и EXCEL для проверки орфографии текстовой информации. Говоря точнее, АК производят автоматически лишь обнаружение ошибок, а собственно коррекция ведется обычно при участии человека. 1. ...
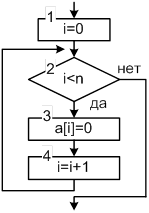
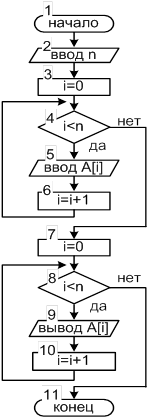
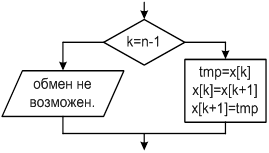
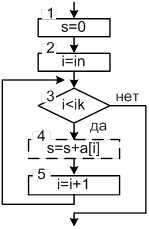
... с условием задачи; 4) выводить исходные данные и результаты вычислений. Исходные данные для отладки программы выбрать самостоятельно. Массив объявить как статический. Задание: В одномерном массиве A размерностью n, найти количество чисел, меньших заданного X, и произведение отрицательных чисел, стоящих на четных местах. Решение Таблица соответствия переменных Переменные в задаче Имя ...
0 комментариев