Российский Государственный Социальный Университет
Факультет Социальных информационных технологий
Кафедра Информационной безопасности
Курсовая работа
по дисциплине
Системы и сети связи
Москва – 2006
Задание 1
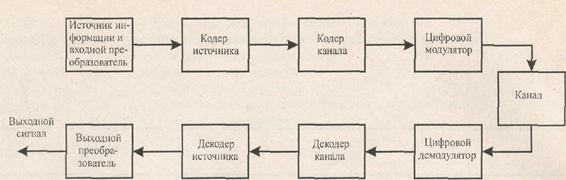
Для системы связи (СС) с переспросом с ожиданием ответа одностороннего действия (рис. 1) при заданных исходных данных:
1. Найти двоичный циклический (n,k)-код Хэмминга, который обеспечивает передачу сообщений в СС с вероятностью выдачи ложного сообщения Рлс(n,k) < Pдоп при следующих условиях:
¾ прямой дискретный канал в СС является двоичным симметричным каналом (ДСК) с постоянными параметрами;
¾ обратный непрерывный канал – без помех;
¾ код используется только для обнаружения ошибок;
¾ найденный значения n и k должны обеспечивать минимум разности Pдоп -Рлс(n,k) для возможных значений n и k.
2. Отложить в координатных осях вычисленные значения Рлс(n,k) для всех исследованных пар (n,k). В этих же осях прямой линией изобразить заданное значение Pдоп.
Исходные данные для курсовой работы (вариант №22):| Вероятность искажения двоичного символа p | 6x10-4 |
| Допустимая вероятность ложного сообщения Pдоп | 2x10-7 |
| Допустимое число переспросов s | ∞ |
| Разрядность кода n | >10 |
| Порождающий многочлен gi(x) | g3(x) |
| Тип кодера | КД 1 |
| Ввод информационных символов в кодер | последовательно |
| Тип декодера | ДК 2 |
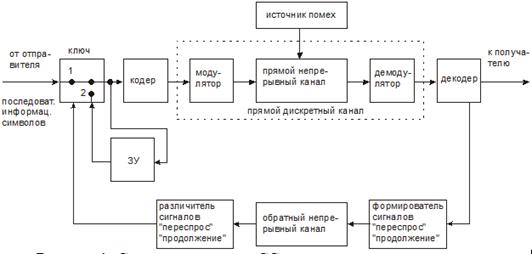
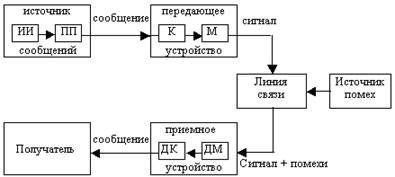
Рисунок 1. Структурная схема СС с переспросом с ожиданием ответа одностороннего действия
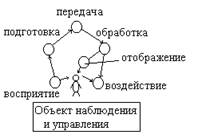
Описание работы СС с переспросом с ожиданием ответа одностороннего действия (рис. 1):
Информационная последовательность отдельными комбинациями не корректирующего кода через первое положение ключа направляется в кодер и в ЗУ передатчика. На выходе кодера образуется комбинация корректирующего кода, которая поступает в модулятор прямого канала. В прямом канале возможно искажение сигнала. На приемной стороне решение о принятом символе принимается демодулятором с так называемой зоной ненадежности.
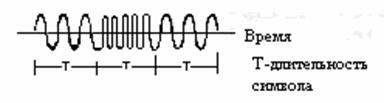
Принцип его работы можно понять из рисунка.
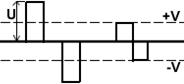
Пусть символ «1» передается по каналу связи импульсом положительной полярности с амплитудой U, а «0» импульсом отрицательной полярности с той же амплитудой.
В демодуляторе выделена некоторая зона +V –V, если принимаемый импульс попадает в эту зону (зона ненадежности), то демодулятор считает, что он не может принять надежного решения, о том, какой символ передавался. В этом случае, демодулятор выдает символ ненадежности Z. С выхода демодулятора комбинации поступают на вход декодера. После поступления всей комбинации с выхода декодера в обратный канал направляется одна из двух команд:
¾ «переспрос», если содержатся ошибки в принятой комбинации, и одновременно кодовое слово с символами Z стирается;
¾ «продолжение», если не обнаружено ошибок, и комбинация не корректирующего кода направляется к получателю.
Если различитель команд получает команду «продолжения», то из ЗУ передатчика в прямой канал направляется следующая порция* информации. Если различитель команд получает команду «переспрос», то он переключает ключ в положение 2 и из ЗУ передатчика в прямой канал повторно направляется комбинация, которая была стерта.
После выдачи в прямой канал из ЗУ передатчика очередной порции информации, следующая порция не передаётся до тех пор, пока не будет получен ответ по этой порции.
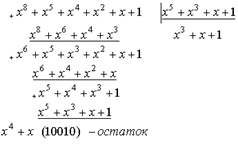
Порядок расчета Рлс и пример расчета Рлс для циклического (n,k)–кода Хэмминга, обеспечивающего минимум разности Рдоп – Рлс(n,k):Произведем расчет для (18,13)-кода с d=3.
Для этого введем обозначения:
· Pбо – вероятность появления на выходе ДСК комбинации (n,k)-кода без ошибок при однократной передаче;
· Роо – вероятность появления на выходе ДСК комбинации (n,k)-кода с обнаруживаемыми ошибками при однократной передаче;
· Рно – вероятность появления на выходе ДСК комбинации (n,k)-кода с необнаруживаемыми ошибками при однократной передаче;
· Рi£vо – вероятность появления на выходе ДСК комбинации с ошибками кратности i£v0;
· Рi>vо – вероятность появления на выходе ДСК комбинации с ошибками кратности i>v0, которые расположены так, что обнаруживаются кодом;
· Рлс – вероятность появления на выходе СС с неограниченным числом переспросов ложного сообщения.
Найдем:
хэмминг код цикличный программа
Pбо = qn, где q=1-p;
Рi£vо =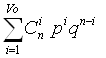 , где v0=d-1;
, где v0=d-1;
Роо = Рi£vо + Рi>vо;
Рно £ 1- Pбо - Рi£vо;
Рлс = Рно/(1- Роо).
Пример:
Pбо = qn=0,999418=0,98925490, где q=1-p=0,9994;
Рi£vо = =
=![]() +
+![]() =
=
18*0,0006*0,98984881+153*0,00000036*0,99044307=0,01074492, где v0=d-1=2;
Роо = Рi£vо + Рi>vо= 0,01074492;
Рно £ 1- Pбо - Рi£vо=1-0,98925490-0,01074492=0,00000018;
Рлс = Рно/(1- Роо)=0,00000018/(1-0,01074492)=0,00000018.
Структурная схема алгоритма расчета кода, ее описание
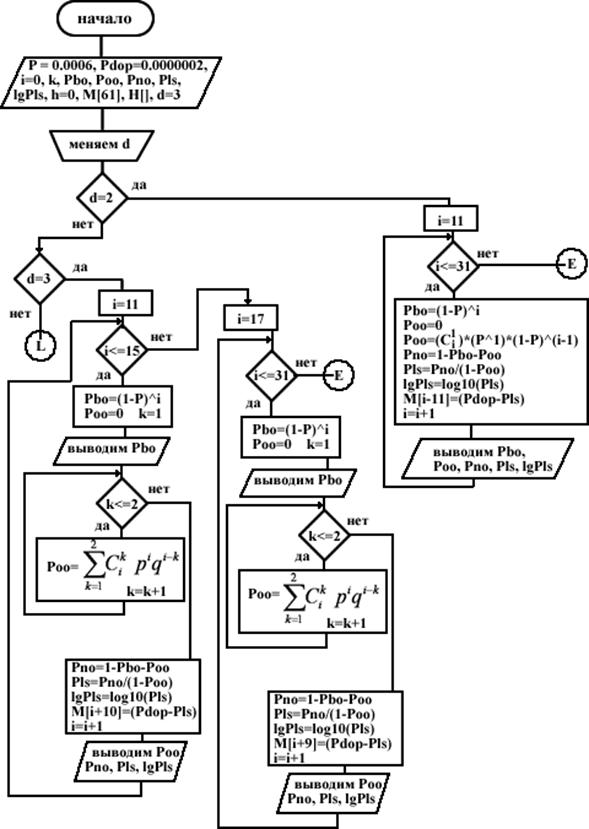
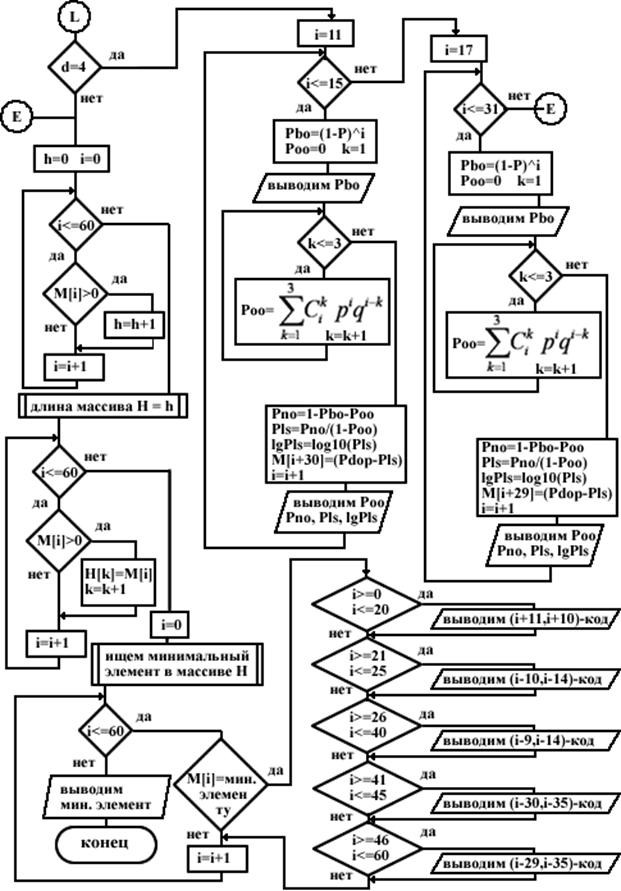
Описание алгоритма:
1) Начало;
2) Объявляем P = 0.0006, Pdop=0.0000002, i=0, k, Pbo, Poo, Pno, Pls, lgPls, h=0, M[61], H[], d=3;
3) Вручную меняем d (по умолчанию d=3);
4) Если d=2, то i=11, иначе переходим к шагу 7;
5) Если i<=31, то Pbo=(1-P)^i, Poo=0, Poo=(C )*(P^1)*(1-P)^(i-1),
Pno=1-Pbo-Poo, Pls=Pno/(1-Poo), lgPls=log10(Pls),
M[i-11]=(Pdop-Pls), i=i+1, переходим к шагу 5, иначе переходим к шагу 35;
6) Выводим Pbo, Poo, Pno, Pls, lgPls, переходим к шагу 5;
7) Если d=3, то i=11, иначе переходим к шагу 21;
8) Если i<=15, то Pbo=(1-P)^i, Poo=0, k=1, иначе переходим к шагу 14;
9) Выводим Pbo;
10) Если k<=2, то Poo= , иначе переходим к шагу 12;
, иначе переходим к шагу 12;
11) k=k+1, переходим к шагу 10;
12) Pno=1-Pbo-Poo, Pls=Pno/(1-Poo), lgPls=log10(Pls),
M[i+10]=(Pdop-Pls), i=i+1;
13) Выводим Poo, Pno, Pls, lgPls, переходим к шагу 8;
14) i=17;
15) Если i<=31, то Pbo=(1-P)^i, Poo=0, k=1, иначе переходим к шагу 35;
16) Выводим Pbo;
17) Если k<=2, то Poo= , иначе переходим к шагу 19;
, иначе переходим к шагу 19;
18) k=k+1, переходим к шагу 17;
19) Pno=1-Pbo-Poo, Pls=Pno/(1-Poo), lgPls=log10(Pls),
M[i+10]=(Pdop-Pls), i=i+1;
20) Выводим Poo, Pno, Pls, lgPls, переходим к шагу 15;
21) Если d=4, то i=11, иначе переходим к шагу 35;
22) Если i<=15, то Pbo=(1-P)^i, Poo=0, k=1, иначе переходим к шагу 28;
23) Выводим Pbo;
24) Если k<=3, то Poo=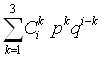 , иначе переходим к шагу 26;
, иначе переходим к шагу 26;
25) k=k+1, переходим к шагу 24;
26) Pno=1-Pbo-Poo, Pls=Pno/(1-Poo), lgPls=log10(Pls),
M[i+10]=(Pdop-Pls), i=i+1;
27) Выводим Poo, Pno, Pls, lgPls, переходим к шагу 22;
28) i=17;
29) Если i<=31, то Pbo=(1-P)^i, Poo=0, k=1, иначе переходим к шагу 35;
30) Выводим Pbo;
31) Если k<=3, то Poo=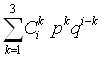 , иначе переходим к шагу 33;
, иначе переходим к шагу 33;
32) k=k+1, переходим к шагу 31;
33) Pno=1-Pbo-Poo, Pls=Pno/(1-Poo), lgPls=log10(Pls),
M[i+10]=(Pdop-Pls), i=i+1;
34) Выводим Poo, Pno, Pls, lgPls, переходим к шагу 29;
35) h=0, i=0;
36) Если i<=60, то переходим к шагу 37, иначе переходим к шагу 38;
37) Если M[i]>0, то h=h+1, i=i+1, иначе i=i+1 и переходим к шагу 36;
38) Выделяем память под массив Н из h элементов.
39) Если i<=60, то переходим к шагу 40, иначе переходим к шагу 41;
40) Если M[i]>0, то H[k]=M[i], k=k+1, i=i+1, иначе i=i+1 и переходим к шагу 39;
41) i=0;
42) Ищем минимальный элемент в массиве Н;
43) Если i<=60, то переходим к шагу 44, иначе переходим к шагу 50;
44) Если M[i]=минимальному элементу, то и переходим к шагу 45, иначе i=i+1 и переходим к шагу 43;
45) Если i>=0 и i<=20, то выводим (i+11,i+10)-код, иначе переходим к шагу 46;
46) Если i>=21 и i<=25, то выводим (i-10,i-14)-код, иначе переходим к шагу 47;
47) Если i>=26 и i<=40, то выводим (i-9,i-14)-код, иначе переходим к шагу 48;
48) Если i>=41 и i<=45, то выводим (i-30,i-35)-код, иначе переходим к шагу 49;
49) Если i>=46 и i<=60, то выводим (i-29,i-35)-код, иначе i=i+1 и переходим к шагу 39;
50) Выводим минимальный элемент из массива Н, как минимум разницы Рдоп-Рлс;
51) Конец.
Распечатка программыПрограмма написана на языке С++.
#include <vcl.h>
#include <math.h>
#include <stdio.h>
#include <vector>
#include <algorithm>
#pragma hdrstop
#include "Unit1.h"
//---------------------------------------------------------------------------
#pragma package(smart_init)
#pragma resource "*.dfm"
float P = 0.0006;
float Pdop = 0.0000002;
using namespace std;
float M[61];
vector<float>H;
char B[128];
TForm1 *Form1;
//---------------------------------------------------------------------------
__fastcall TForm1::TForm1(TComponent* Owner)
: TForm(Owner)
{
}
//---------------------------------------------------------------------------
float C(int n,int m)
{float c=1.0;
for(int i=n;i>=n-m+1;i--)c*=i;
for(int i=1;i<=m;i++)c/=i;
return (int)c;
}
void __fastcall TForm1::ComboBox1Select(TObject *Sender)
{int i=0, k;
double Pbo,Poo,Pno,Pls,lgPls;
AnsiString s;
ListBox1->Clear();
ListBox2->Clear();
ListBox3->Clear();
ListBox4->Clear();
ListBox5->Clear();
ListBox6->Clear();
ListBox7->Clear();
//d=2
if(ComboBox1->ItemIndex==0)
for(i=11;i<=31;i++)
{s="("+IntToStr(i)+","+IntToStr(i-1)+")";
ListBox1->Items->Add(s);
Pbo=pow(1-P,i);
sprintf(B,"%.8f",Pbo);
ListBox2->Items->Add(B);
Poo=0;
Poo=C(i,1)*pow(P,1)*pow(1-P,i-1);
sprintf(B,"%.8f",Poo);
ListBox3->Items->Add(B);
Pno=1-Pbo-Poo;
sprintf(B,"%.8f",Pno);
ListBox4->Items->Add(B);
Pls=Pno/(1-Poo);
sprintf(B,"%.8f",Pls);
ListBox5->Items->Add(B);
lgPls=log10(Pls);
sprintf(B,"%.2f",lgPls);
ListBox6->Items->Add(B);
Series1->AddXY(i,lgPls,s,clRed);
M[i-11]=(Pdop-Pls);
}
//d=3
if(ComboBox1->ItemIndex==1)
{for(i=11;i<=15;i++)
{s="("+IntToStr(i)+","+IntToStr(i-4)+")";
ListBox1->Items->Add(s);
Pbo=pow(1-P,i);
sprintf(B,"%.8f",Pbo);
ListBox2->Items->Add(B);
Poo=0;
for(k=1;k<=2;k++)
Poo+=C(i,k)*pow(P,k)*pow(1-P,i-k);
sprintf(B,"%.8f",Poo);
ListBox3->Items->Add(B);
Pno=1-Pbo-Poo;
sprintf(B,"%.8f",Pno);
ListBox4->Items->Add(B);
Pls=Pno/(1-Poo);
sprintf(B,"%.8f",Pls);
ListBox5->Items->Add(B);
lgPls=log10(Pls);
sprintf(B,"%.2f",lgPls);
ListBox6->Items->Add(B);
Series2->AddXY(i,lgPls,s,clLime);
M[i+10]=(Pdop-Pls);
}
for(i=17;i<=31;i++)
{s="("+IntToStr(i)+","+IntToStr(i-5)+")";
ListBox1->Items->Add(s);
Pbo=pow(1-P,i);
sprintf(B,"%.8f",Pbo);
ListBox2->Items->Add(B);
Poo=0;
for(k=1;k<=2;k++)
Poo+=C(i,k)*pow(P,k)*pow(1-P,i-k);
sprintf(B,"%.8f",Poo);
ListBox3->Items->Add(B);
Pno=1-Pbo-Poo;
sprintf(B,"%.8f",Pno);
ListBox4->Items->Add(B);
Pls=Pno/(1-Poo);
sprintf(B,"%.8f",Pls);
ListBox5->Items->Add(B);
lgPls=log10(Pls);
sprintf(B,"%.2f",lgPls);
ListBox6->Items->Add(B);
Series2->AddXY(i,lgPls,s,clLime);
M[i+9]=(Pdop-Pls);
}
}
//d=4
if(ComboBox1->ItemIndex==2)
{for(i=11;i<=15;i++)
{s="("+IntToStr(i)+","+IntToStr(i-5)+")";
ListBox1->Items->Add(s);
Pbo=pow(1-P,i);
sprintf(B,"%.8f",Pbo);
ListBox2->Items->Add(B);
Poo=0;
for(k=1;k<=3;k++)
Poo+=C(i,k)*pow(P,k)*pow(1-P,i-k);
sprintf(B,"%.8f",Poo);
ListBox3->Items->Add(B);
Pno=1-Pbo-Poo;
sprintf(B,"%.8f",Pno);
ListBox4->Items->Add(B);
Pls=Pno/(1-Poo);
sprintf(B,"%.8f",Pls);
ListBox5->Items->Add(B);
lgPls=log10(Pls);
sprintf(B,"%.2f",lgPls);
ListBox6->Items->Add(B);
Series3->AddXY(i,lgPls,s,clYellow);
M[i+30]=(Pdop-Pls);
}
for(i=17;i<=31;i++)
{s="("+IntToStr(i)+","+IntToStr(i-6)+")";
ListBox1->Items->Add(s);
Pbo=pow(1-P,i);
sprintf(B,"%.8f",Pbo);
ListBox2->Items->Add(B);
Poo=0;
for(k=1;k<=3;k++)
Poo+=C(i,k)*pow(P,k)*pow(1-P,i-k);
sprintf(B,"%.8f",Poo);
ListBox3->Items->Add(B);
Pno=1-Pbo-Poo;
sprintf(B,"%.8f",Pno);
ListBox4->Items->Add(B);
Pls=Pno/(1-Poo);
sprintf(B,"%.8f",Pls);
ListBox5->Items->Add(B);
lgPls=log10(Pls);
sprintf(B,"%.2f",lgPls);
ListBox6->Items->Add(B);
Series3->AddXY(i,lgPls,s,clYellow);
M[i+29]=(Pdop-Pls);
}
}
int h=0;
for (i=0;i<=60;i++)
if (M[i]>0) h++;
H.resize(h);
k=0;
for (i=0; i<=60;i++)
if (M[i]>0) {H[k]=M[i]; k++;}
for (i=0;i<=60;i++)
if (M[i]==*min_element(H.begin(),H.end()))
{if (i>=0&&i<=20)
{s="("+IntToStr(i+11)+","+IntToStr(i+10)+")-код с d=2";
ListBox7->Items->Add(s);}
if (i>=21&&i<=25)
{s="("+IntToStr(i-10)+","+IntToStr(i-14)+")-код с d=3";
ListBox7->Items->Add(s);}
if (i>=26&&i<=40)
{s="("+IntToStr(i-9)+","+IntToStr(i-14)+")-код с d=3";
ListBox7->Items->Add(s);}
if (i>=41&&i<=45)
{s="("+IntToStr(i-30)+","+IntToStr(i-35)+")-код с d=4";
ListBox7->Items->Add(s);}
if (i>=46&&i<=60)
{s="("+IntToStr(i-29)+","+IntToStr(i-35)+")-код с d=4";
ListBox7->Items->Add(s);}
}
ListBox7->Items->Add("");
ListBox7->Items->Add("Минимальная разность");
sprintf(B,"%.12f",*min_element(H.begin(),H.end()));
ListBox7->Items->Add("Рдоп-Рлс");
ListBox7->Items->Add(B);
}
//---------------------------------------------------------------------------
void __fastcall TForm1::FormCreate(TObject *Sender)
{ComboBox1->ItemIndex=1;
Series4->AddXY(0,log10(Pdop),"lg Pдоп",clBlack);
Series4->AddXY(31.3,log10(Pdop),"lg Pдоп",clBlack);
}
//---------------------------------------------------------------------------
График найденных значений lg Pлс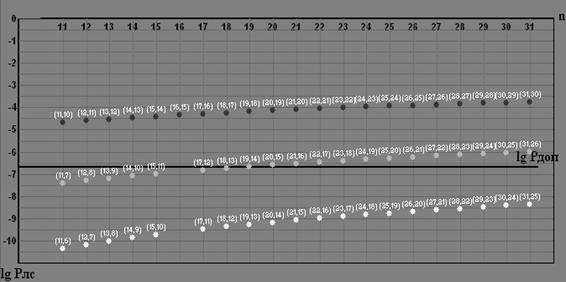
Построить функциональные схемы кодера и декодера для найденного (n,k)-кода и заданного для него порождающего многочлена g3(X). При изображении схем кодера и декодера использовать условные изображения элементов:
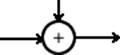
|
элемент умножения |
элемент памяти |
элемент сложения по модулю 2 |
Исходные данные:
g3(x)=x5+x3+x2+x+1;
r=5.
Функциональная схема кодера для (18,13)-кода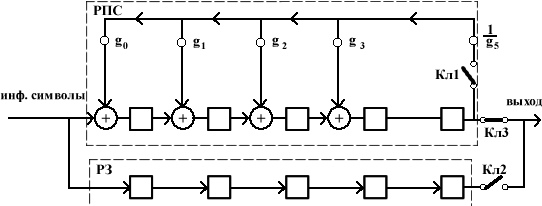
Описание работы схемы:
Кодер 1 с последовательным вводом информационных символов (a12, a11, …, a1, a0) состоит из регистра проверочных символов (РПС), регистра задержки (РЗ) с 5 элементами памяти и трех ключей. В исходном состоянии в элементах памяти регистров – нули, ключи Кл1 и Кл2 разомкнуты, Кл3 замкнут.
При подаче первых 5 импульсов сдвига (ИС) 5 информационных символов, начиная со старшего, вводятся в оба регистра. С окончанием 5-го ИС ключи Кл1 и Кл2 замыкаются, а Кл3 размыкается.
В течение последующих k ИС информационные символы выводятся из РЗ, а в РПС образуются 5 проверочных символов. После этого ключи Кл1 и Кл2 размыкаются, а Кл3 замыкается.
За последующие 5 импульсов сдвига проверочные символы выдаются на выход кодера, после чего схема возвращается в исходное состояние. Таким образом, первый символ комбинации УЦК появляется на выходе кодера с задержкой на 5 ИС.
Функциональная схема декодера для (18,13)-кода
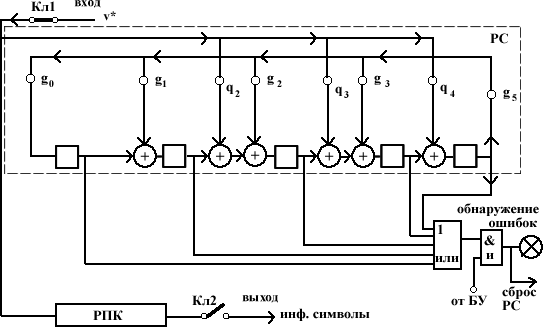
Список использованной литературы
1. Хохлов Г.И., Пособие к выполнению лабораторной работы №3 по дисциплине «Системы и сети связи». – М.: 2005. – 18 с.
2. Хохлов Г.И., Пособие по выполнению курсовой работы по дисциплине «Системы и сети связи». – М.: 2005. – 15 с.
Похожие работы
... , если его длина n=qm-1 над GF(q). Если длина кода меньше длины примитивного кода, то код называется укороченным или непримитивным. Общее свойство кодовых слов циклического кода - это их делимость без остатка на некоторый многочлен g(x), называемый порождающим. Результатом деления двучлена xn+1 на многочлен g(x) является проверочный многочлен h(x). При декодировании циклических кодов используются ...
... , работавших в области электротехники, заинтересовалась возможностью создания технологии хранения данных, обеспечивающей более экономное расходование пространства. Одним из них был Клод Элвуд Шеннон, основоположник современной теории информации. Из разработок того времени позже практическое применение нашли алгоритмы сжатия Хаффмана и Шеннона-Фано. А в 1977 г. математики Якоб Зив и Абрахам Лемпел ...
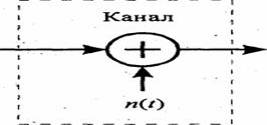
... за которым следует устройство дискретизации (рисунок 4.2), подастся известный сигнал s(t) плюс шум AWGN n(t). 4.4 Межсимвольная интерференция На рисунке 4.3 а) представлены фильтрующие элементы типичной системы цифровой связи. В системе - передатчике, приемнике и канале - используется множество разнообразных фильтров (и реактивных элементов, таких как емкость и индуктивность). В передатчике ...
... для кода исправляющего одиночную ошибку, а также эффективность использования канала связи. Для исправления двукратной ошибки или . (5) Введение избыточности в кодовые комбинации при использовании корректирующих кодов существенно снижает скорость передачи информации и эффективность использования канала связи. Например, для кода (31, 26) скорость передачи информации равна , т. е. ...
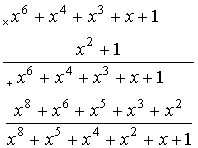
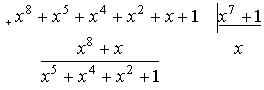



0 комментариев