Навигация
Курс: Теория информации и кодирования
Тема: КОРРЕКТИРУЮЩИЕ КОДЫ
Содержание
1. КОРРЕКТИРУЮЩИЕ КОДЫ. ОСНОВНЫЕ ПОНЯТИЯ
2. ЛИНЕЙНЫЕ ГРУППОВЫЕ КОДЫ
3. КОД ХЭММИНГА
Список Литературы
1. КОРРЕКТИРУЮЩИЕ КОДЫ. ОСНОВНЫЕ ПОНЯТИЯ
В соответствии с теоремой Шеннона для дискретного канала с помехами, вероятность ошибки при передаче данных по каналу связи может быть сколь угодно малой при выборе соответствующего метода кодирования сигнала, т. е. помеха не накладывает существенных ограничений на точность передачи информации (данных). Достоверность передаваемой информации может быть обеспечена применением корректирующих кодов.
Помехоустойчивыми или корректирующими кодами называются коды, позволяющие обнаружить и устранить ошибки при передаче информации из-за воздействия помех.
Наиболее распространенным является класс кодов с коррекцией одиночных и обнаружением двойных ошибок (КО-ОД). Самым известных среди этих кодов является код Хэмминга, имеющий простой и удобный для технической реализации алгоритм обнаружения и исправления одиночной ошибки.
В ЭВМ эти коды используются для повышения надежности оперативной памяти (ОП) и магнитных дисков. Число ошибок в ЭВМ зависит от типа неисправностей элементов схем (например, неисправность одного элемента интегральной схемы (ИС) вызывает одиночную ошибку, а всей ИС ОП - кратную). Для обнаружения кратных ошибок используется код КО-ОД-ООГ (коррекция одиночной, обнаружение двойной и обнаружение кратной ошибки в одноименной группе битов).
Среди корректирующих кодов широко используются циклические коды, в ЭВМ эти коды применяются при последовательной передаче данных между ЭВМ и внешними устройствами, а также при передаче данных по каналам связи. Для исправления двух и более ошибок (d0 ³ 5) используются циклические коды БЧХ (Боуза - Чоудхури - Хоквингема), а также Рида-Соломона, которые широко используются в устройствах цифровой записи звука на магнитную ленту или оптические компакт-диски и позволяющие осуществлять коррекцию групповых ошибок. Способность кода обнаруживать и исправлять ошибки достигается за счет введений избыточности в кодовые комбинации, т. е. кодовым комбинациям из к двоичных информационных символов, поступающих на вход кодирующего устройства, соответствует на выходе последовательность из n двоичных символов (такой код называется (n, k) - кодом).
Если N0 = 2n-общее число кодовых комбинаций, а N = 2k - число разрешенных, то число запрещенных кодовых комбинаций равно
N0-N = 2n -2k.
При этом число ошибок, которое приводит к запрещенной кодовой комбинации равно:
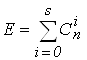 , (1)
, (1)
где S - кратность ошибки, т. е. количество искаженных символов в кодовой комбинации S = 0, 1, 2, ...
Cni- сочетания из n элементов по i, вычисляемое по формуле:
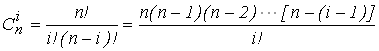 , (2)
, (2)
для S = 0 ; ![]()
S = 1 ; ![]()
S = 2 ; ![]()
S = 3 ; ![]() и т. д.
и т. д.
Для исправления S ошибок количество комбинаций кодового слова, составленного из m проверочных разрядов N = 2m, должно быть больше возможного числа ошибок (2), при этом количество обнаруживаемых ошибок в два раза больше, чем исправляемых
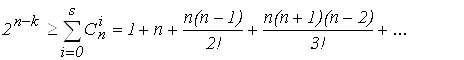 (3)
(3)
2m ³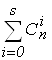 откуда
откуда 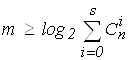 .
.
Для одиночной ошибки, как наиболее вероятной ![]() .
.
В зависимости от исходных данных кода (n или k) можно использовать
формулы
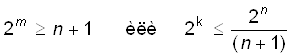 . (4)
. (4)
При этом, m = [log2(1+n)] или m = [log2 {(k+1)+ [log2(k+1)]}], где ква-дратные скобки обозначают округление до большего целого.
В таблице 1 приведены соотношения между длиной кодовой комбинации и количеством информационных и контрольных разрядов для кода исправляющего одиночную ошибку, а также эффективность использования канала связи.
Для исправления двукратной ошибки
![]() или
или ![]() . (5)
. (5)
Введение избыточности в кодовые комбинации при использовании корректирующих кодов существенно снижает скорость передачи информации и эффективность использования канала связи.
Например, для кода (31, 26) скорость передачи информации равна
![]() ,
,
т. е. скорость передачи уменьшается на 16%.
Таблица 1| n | 7 | 10 | 15 | 31 | 63 | 127 | 255 |
| k | 4 | 6 | 11 | 26 | 57 | 120 | 247 |
| m | 3 | 4 | 4 | 5 | 6 | 7 | 8 |
|
| 0,57 | 0,6 | 0,75 | 0,84 | 0,9 | 0,95 | 0,97 |
Как видно из таблицы 1, чем больше n, тем эффективнее используется канал.
Пример 1. Определить количество проверочных разрядов для систематического кода исправляющего одиночную ошибку и состоящего из 20 информационных разрядов.
Решение: Общая длина кодовой комбинации равна n = k+m, где k- количество информационных разрядов, а m- проверочных разрядов.
Для обнаружения двойной и исправления одиночной ошибки зависимости для разрядов имеют вид 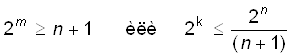 , при этом
, при этом
m = [log2 {(k+1)+ [log2(k+1)]}]=[log2 {(20+1)+ [log2(20+1)]}]=5,
т. е. получим (25, 20)-код.
Похожие работы
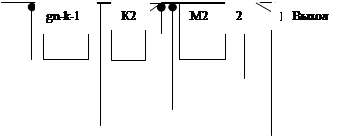
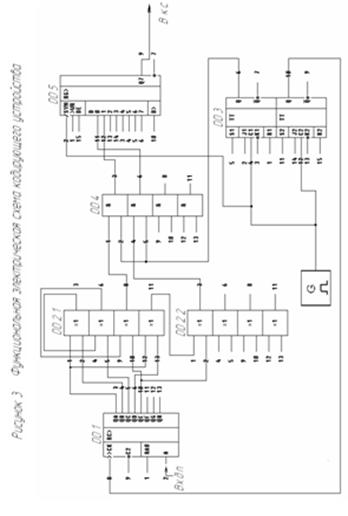
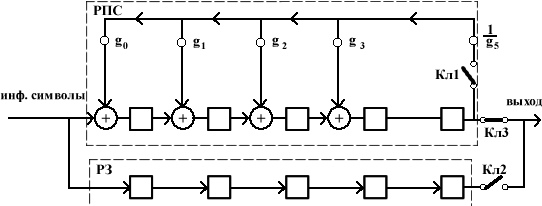
... обратной связи не через n-k сдвигов, а сразу с первого такта. Это позволяет устранить разрыв между информационными и проверочными символами. Рис. 1.1. Кодирующее устройство для циклического кода на основе (n-k) – разрядного регистра сдвига. В исходном состоянии ключ К1 находится в положении 1, а ключ К2 замкнут. Информационные символы одновременно поступают как ...
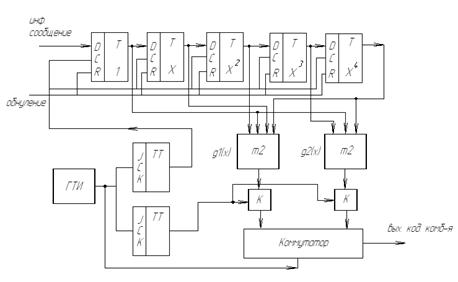
... по методу максимального правдоподобия, то есть оптимальным образом. Оптимальное декодирование предполагает, что декодер будет исправлять большее число ошибок, чем пороговое значение. 2. Разработка кодирующего устройства для формирования сверточного кода 2.1 Разработка структурной схемы кодирующего устройства для формирования сверточного кода Основой для построения структурной ...
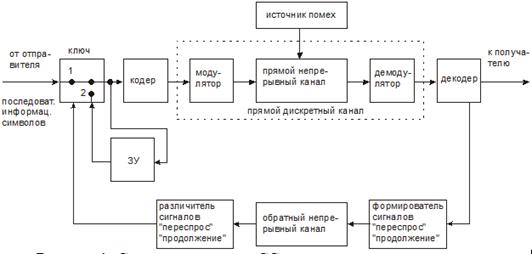
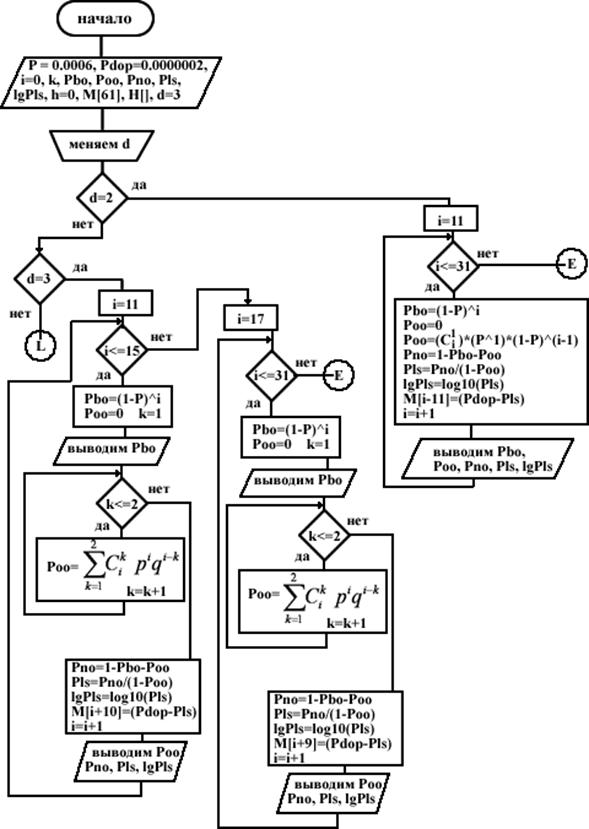
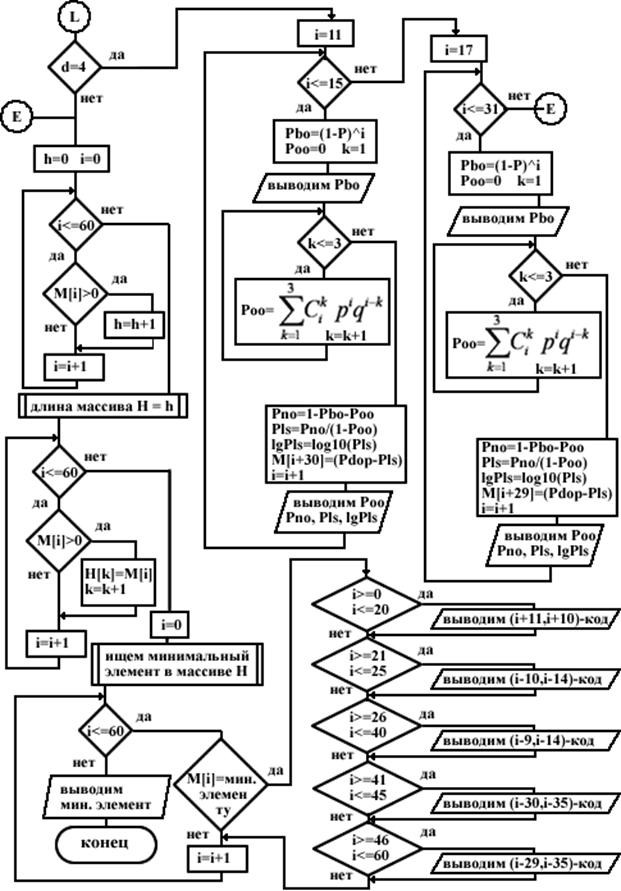
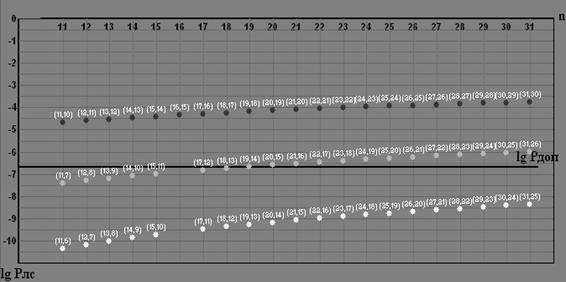
... из ЗУ передатчика очередной порции информации, следующая порция не передаётся до тех пор, пока не будет получен ответ по этой порции. Порядок расчета Рлс и пример расчета Рлс для циклического (n,k)–кода Хэмминга, обеспечивающего минимум разности Рдоп – Рлс(n,k): Произведем расчет для (18,13)-кода с d=3. Для этого введем обозначения: · Pбо – вероятность появления на выходе ДСК комбинации ...
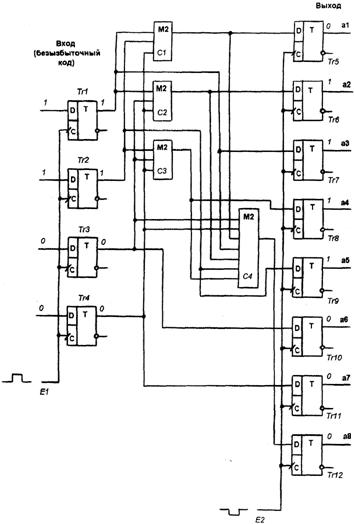
... , ещё одно: Мы получили окончательные правила построения кода, способного исправлять все одиночные и обнаруживать двойные ошибки: Используя правила построения корректирующего кода (*), построим таблицу разрешённых комбинаций группового кода объёмом 9 слов, способного исправлять все одиночные и обнаруживать двойные ошибки. В колонку «безызбыточный код» записываем девять (по заданию Q=9) ...
0 комментариев