Навигация
З'єднання фаз навантаження трикутником
4. З'єднання фаз навантаження трикутником
трифазний генератор коло потужність
Складемо розрахункову схему при з'єднанні навантаження трикутником (рис.4.15). При цьому:
iА, iВ, iС – лінійні струми навантаження, А;
iaв, ibc, ica – фазні струми навантаження, А;
![]() ,
, ![]() ,
, ![]() – лінійні (фазні) напруги навантаження, В.
– лінійні (фазні) напруги навантаження, В.
Як видно з розрахункової схеми, фазна напруга навантаження дорівнює лінійній напрузі навантаження, тобто
Uф = Uл .
За першим законом Кірхгофа знайдемо лінійні струми через фазні:
iА = iab – ica ;
iВ = ibc – iab ;
iС = ica – ibc .
Встановимо зв'язок між діючими значеннями фазних (Iф) і лінійних (Iл) струмів навантаження при з'єднанні його фаз трикутником, для чого розглянемо трикутник струмів (рис.4.17), який одержано з векторної діаграми.
З трикутника струмів знаходимо:
Iл = 2 Iф cos 30° = 2 Iф![]() =
= ![]() Iф .
Iф .
5. Потужності трифазного кола
Кожна фаза трифазного навантаження споживає активну, реактивну і повну потужності. При симетричному навантаженні та схемі з'єднання фаз навантаження зіркою ці потужності в кожній фазі можна розрахувати в такий спосіб:
![]() ;
;
![]() ;
;
![]() .
.
Потужності, які споживають три фази навантаження, можна розрахувати, помноживши на кількість фаз навантаження (тобто на три) потужності, які споживає одна фаза:
![]() ;
;
![]() ;
;
![]() .
.
Визначимо ці потужності через лінійні напруги і струми:
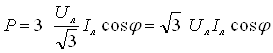 ;
;
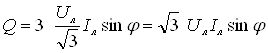 ;
;
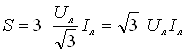 .
.
При з'єднанні фаз навантаження трикутником вирази (4.28) і (4.29) справедливі, тільки в цих виразах будуть свої фазні струми і напруги. Визначимо ці потужності через лінійні напруги і струми:
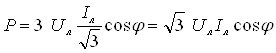 ;
;
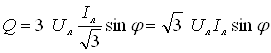 ;
;
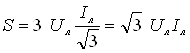 .
.
Таким чином, потужності, які споживає трифазне навантаження (незалежно від схеми його з'єднання), можна розрахувати в такий спосіб:
![]() ;
;
![]() ;
;
![]() .
.
6. Розрахунок нерозгалужених трифазних кіл синусоїдного струму
Розглянемо розрахункову схему трифазного трипровідного електричного кола, яке складається з ідеального генератора, з'єднаного зіркою, ідеальної лінії електропередачі, навантаження, з'єднаного зіркою (рис.4.18).
Нехай задано діюче значення електрорушійної сили Е в фазі симетричного генератора і повні опори фаз навантаження
![]() ,
,
а також коефіцієнти потужності фаз навантаження
cos jа = cos jb = cos jс = cos j .
Потрібно розрахувати діючі значення фазних і лінійних сил струмів генератора і навантаження, фазних і лінійних напруг генератора і навантаження, а також потужності, які віддаються генератором і споживаються навантаженням.
Алгоритм розрахунку наступний:
1. Складаємо розрахункову схему однієї фази кола.
Приймаємо, що потенціал точки 0 дорівнює нулю. Можна довести, що при симетричному режимі роботи кола потенціал точки 0’ також дорівнює нулю.
Тому можна з'єднати точки 0 і 0’, від чого режим роботи кола не зміниться.
Виділяємо одну фазу кола (рис.4.19).
2. Визначаємо діючі значення сил струмів.
У даному випадку фазний струм генератора дорівнює лінійному струму і дорівнює фазному струму навантаження. Наприклад, для фази А він дорівнює:
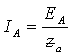 .
.
Інші струми Iв і Iс дорівнюють струму Iа.
3. Визначаємо діючі значення фазних напруг.
У даному випадку фазні напруги генератора дорівнюють фазним напругам навантаження. Наприклад, для фази а воно дорівнює:
![]() .
.
Інші напруги Uа, Uв, Uс, Ub, Uс дорівнюють Uа.
4. Визначаємо діючі значення лінійних напруг.
У даному випадку лінійні напруги генератора дорівнюють лінійним напругам навантаження. Наприклад:
![]() .
.
Інші напруги Uав, Uвс, Uса, Ubс, Uса дорівнюють Uаb.
5. Визначаємо активну потужність.
У даному випадку активна потужність, яка віддається генератором, дорівнює активної потужності, яку споживає навантаження:
![]()
![]() ,
,
де Uф і Uл – відповідно фазна і лінійна напруги, В;
Iф і Iл – відповідно фазний і лінійний струми, А.
Похожие работы
... ється в p і n областях: lp-n = lp + ln: , звідси , де ε – відносна діелектрична проникність матеріалу напівпровідника; ε0 — діелектрична постійна вільного простору. Товщина електронно-діркових переходів має порядок (0,1-10)мкм. Якщо , то і p-n-перехід називається симетричним, якщо , то і p-n-перехід називається несиметричним, причому він в основному розташовується у області напі ...
0 комментариев