Аналіз вимог до точності та стійкості слідкувальної системи

Аналіз вимог до точності та стійкості слідкувальної системи Аналіз інформаційних процесів предметної області дослідження Функціональна схема та математична модель слідкувальної системи

50871

знак

таблиц

изображений

Модель дослідження стійкості та якості перехідних процесів слідкувальної системи Читать далее: Аналіз інформаційних процесів предметної області дослідження

1.2 Аналіз вимог до точності та стійкості слідкувальної системи

Точність системи автоматичного управління, одна з найважливіших характеристик систем автоматичного управління (САУ), що визначає міру наближення реального керованого процесу (КП) до потрібного. Відхилення КП від потрібного викликається динамічними властивостями об'єкту управління (ОУ) і САУ, помилками вимірювальних і виконавчих пристроїв, що входять в САУ, внутрішніми шумами в деяких її елементах і зовнішніми перешкодами. Воно складається з систематичної і випадкової помилок. Систематична помилка є математичним чеканням випадкового відхилення КП від потрібного. Випадкова помилка зазвичай характеризується дисперсією або середнім квадратичним відхиленням (в разі одновимірного КП) або кореляційною матрицею (в разі багатовимірного КП). Співвідношення між систематичною і випадковою помилками визначається смугою пропускання системи (діапазоном частот коливань вхідного сигналу, на які система помітно реагує). З розширенням смуги пропускання система стає менш інерційною і систематична помилка зменшується, проте при цьому збільшується дисперсія випадкової помилки. Тому при проектуванні САУ шукають деяке компромісне рішення задачі вибору смуги пропускання. Точність тісно пов'язана з іншою важливою характеристикою САУ - її чутливістю.

На початковому етапі розвитку автоматики питання про облік випадкових помилок не виникало і точність САУ характеризували лише систематичною помилкою. Необхідність обліку випадкових помилок, що виникла вперше при вирішенні завдань прицілювання при стрілянині і бомбометанні з літака і збільшена з появою радіолокації, привела до створення і розвитку статистичної теорії КП, яка стала одннм з найважливіших напрямів теорії автоматичного управління. Основні завдання статистичної теорії КП: 1) розрахунок точності при заданих характеристиках ОУ, САУ і випадкових обурень - статистичний аналіз САУ; 2) визначення оптимальних характеристик САУ, при яких досягається найбільша можлива точність при заданих статистичних характеристиках сигналів управління і перешкод, - статистичний синтез САУ. Статистична теорія КП дає методи статистичного аналізу і синтезу систем різних класів (лінійних, таких, що приводяться до лінійних, описуваних стохастичними диференціальними або різницевими рівняннями), а також загальні методи оптимізації лінійних і нелінійних систем по різних критеріях і методи визначення гранично досяжною (потенційною) точністю при заданих статистичних характеристиках корисних сигналів і перешкод. Методи статистичної теорії КП складні і вимагають вживання ЕОМ.

Управління складними системами зазвичай здійснюється в умовах невизначеності - за відсутності достатньої інформації про характеристики

корисних сигналів і перешкод, а в деяких випадках і про ОУ. Тому виникає проблема підвищення точності САУ безпосередньо в процесі її роботи. Це досягається вживанням принципів адаптації, вчення або самонавчання. Статистична теорія УП дає теоретичні підстави для проектування адаптивних (зокрема самоналагоджувальних), таких, що вчаться і самонавчальних САУ, а також методи оцінки ефективності вчення - підвищення їх точності. Розвиток статистичної теорії КП привів до створення на початку 70-х рр. 20 ст. основ теорії стохастичних систем, поширюючий і узагальнювальний методи статистичної теорії КП (у тому числі методи розрахунку точності) на системи, що включають не лише машини, автоматичні пристрої і ЕОМ, але і колективи людей.

ССП підрозділяють на пошукові та без пошукові. У пошукових ССП необхідна якість управління досягається в результаті автоматичного пошуку оптимального (в деякому розумінні) налаштування. Якість налаштування характеризується деяким узагальненим показником, пов'язаним з первинними параметрами налаштування складним, зазвичай не цілком стабільним і недостатньо відомим співвідношенням. Цей показник вимірюється безпосередньо або обчислюється по виміряних значеннях первинних параметрів. Параметрам налаштування в ССП надають пошукові або пробні зміни. Аналіз коливань показника якості налаштування, викликаних пошуковими діями, дозволяє встановити, чи є налаштування оптимальним, тобто відповідною екстремуму (максимуму або мінімуму) показника якості. Якщо мають місце відхилення від екстремуму, то налаштування змінюється до тих пір, поки не наблизиться до оптимальної. Пошукові ССП можуть працювати при зміні зовнішніх умов в широких межах.

Без пошукові ССП мають перед пошуковими системами певну перевагу, обумовлену тим, що пошук оптимального стану віднімає значний час, тобто час само настройки пошукових систем обмежений знизу. У без пошукових ССП використовується деякий контрольований показник якості управління (наприклад, значення похідної контрольованого параметра за часом). Автоматичним налаштуванням параметрів цей показник підтримується в заданих межах. Залежно від вигляду показника розрізняють ССП з контролем перехідних процесів, з контролем частотних характеристик, з еталонною моделлю і ін. Все це - замкнуті без пошукові ССП із замкнутим контуром само настройки, в якому параметри налаштування автоматично змінюються при виході показника якості за допустимі межі. Деякі замкнуті без пошукові ССП близькі до звичайних нелінійних систем автоматичного управління із зниженою чутливістю до характеристик об'єкту - до таких, наприклад, як релейні системи або управління системи із змінною структурою. Поряд із замкнутими застосовують також розімкнені ССП - , наприклад, системи параметричної компенсації. У цих ССП контролюються дії, що викликають зміну властивостей об'єкту, і за заздалегідь розрахованою програмою змінюються параметри налаштування системи; контур само настройки в цьому випадку розімкнений. Така само настройка може бути майже миттєвою, проте її здійснення вимагає контролю довкілля і досить точного знання законів дії середовища на керований об'єкт. [3]

Само настройка реалізується як спеціальною апаратурою (у вигляді блоків само настройки або самоналагоджувальних екстремальних регулювальників), так і адаптивними алгоритмами центральних керуючих ЦВМ. Додання алгоритмам управління властивостей само настройки (адаптації) істотно розширює можливості управління всілякими процесами. Впровадження ССП дозволяє наблизитися до оптимальних режимів функціонування об'єктів, полегшує завдання уніфікації систем управління, скорочує час на випробування і наладку, знижує технологічні вимоги на виготовлення ряду вузлів пристроїв управління, звільняє обслуговуючий персонал від трудомістких операцій налаштування. Практичне використання ССП і самоналагоджувальних алгоритмів - одна з характерних меж технічного прогресу в області управління.

У статичному режимі роботи всі складові вектора стану САУ не залежать від моменту часу їх розгляду і залишаються постійними, відповідними умові рівноваги системи. Це стан залежно від структури і параметрів САУ може бути стійким або нестійким. Якщо після зміни вектора зовнішніх дій система приходить в стан, при якому всі складові вектора її стану стають постійними, тобто система повертається в положення рівноваги, то це стан рівноваги є стійким. У разі, коли після зміни вхідного сигналу або збурення, система не прагне в первинний стан, а вектор вихідних сигналів змінюється незалежно від зовнішньої дії, то такий стан є нестійким. В цьому випадку система автоматичного управління є нестійкою. Графічна інтерпретація таких режимів роботи САУ представлена на рисунок 1.1.

Рисунок 1.1- Графічна інтерпретація стійкості

Під стійкістю розуміється властивість САУ повертатися в початковий стан після виведення її з цього стану і припинення впливу задаючої або збурюючої дії. [2]

Тільки стійка система автоматичного управління може виконувати покладені на неї функції. Тому одним з основних завдань САУ є забезпечення її стійкості.

Основи теорії стійкості САУ були закладені А.М. Ляпуновим в його роботі "Загальне завдання стійкості рухів", опублікованої в 1882 р.

Якщо САУ представляється системою лінійних диференціальних рівнянь, то її стійкість не залежить від величини і точки додатку зовнішніх обурень.

Варто розрізняти стійкість системи управління, системи показників і стійкість функціонування самого підприємства, що залежить від ряду показників, життєвого циклу підприємства й етапу цього життєвого циклу.

Крім того, стійкість управління характеризує розтягнутість циклу управління. Чим оперативність управління вища, тобто відповідно тривалість циклу управління менша, тим і більш ефективний вплив системи управління на поведінку об'єкта.

Важливим фактором стійкості підприємства є його гнучкість, гнучкість системи управління. Під гнучкістю управління розуміється здатність системи пристосовуватися до умов управління, що змінюються.

Нелінійні системи можуть бути стійкі при малих обуреннях і нестійкі при великих обуреннях. Теорема Ляпунова встановлює, що про стійкість нелінійних систем при малих обуреннях можна судити по їх лінеаризованих рівняннях, достатньо адекватно тих, що описують поведінку САУ при малих відхиленнях від положення рівноваги. Тому розглядатимемо тільки питання стійкості САУ, що представляються лінійними або лінеаризованими диференціальними рівняннями.

При порушенні рівноваги САУ, викликаної зовнішнім дія, виникають перехідні процеси. Вид перехідного процесу залежить як від властивостей системи, так і від виду обурення. У перехідному процесі присутні 2 складові: — вільні рухи системи, визначувані початковими умовами і властивостями САУ; вимушені рухи, визначувані обуренням і властивостями системи. Вид перехідного процесу визначається як

Щоб САУ могла достовірно відображати інформацію, що задавалася, необхідно, щоб в перехідному процесі вільна складова з часом повинна прагнути до нуля, тобто повинна виконуватися умова вигляду:

Характер вільного руху системи визначає її стійкість або нестійкість.

Можливі види перехідних процесів в САУ представлені на рисунок. 1.2.

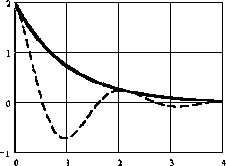
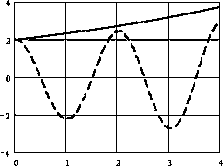
Рисунок 1.2 - Види кривих перехідних процесів

Прямий аналіз стійкості САУ, заснований на обчисленні коріння характеристичного рівняння, пов'язаний з необхідністю обчислення коріння, що є непростим завданням. Тому в інженерній практиці важливого значення набувають правила, що дозволяють визначати стійкість системи без обчислення коріння характеристичного рівняння.

Способи визначення стійкості САУ без обчислення коріння характеристичного рівняння називаються критеріями стійкості САУ. Розрізняють дві групи критеріїв стійкості: алгебра – засновані на аналізі коефіцієнтів характеристичного рівняння, і частотні – засновані на аналізі частотних характеристик САУ.

Критерії стійкості лінійних САУ

Критерій Рауса

Цей критерій є системою нерівностей, складених по особливих правилах з коефіцієнтів характеристичного рівняння замкнутої САУ:

1) У першому рядку таблиці записують коефіцієнти характеристичного рівняння, що мають парні індекси в порядку їх зростання.

2) У другому рядку таблиці записують коефіцієнти з непарними індексами в порядку їх зростання.

3) У подальші рядки вписують коефіцієнти, визначені як

де – i – індекс, що позначає номер рядка таблиці

– індекс, що позначає номер стовпця таблиці.

4) Число рядків таблиці Рауса на одиницю перевищує порядок характеристичного рівняння замкнутої САУ.

Умови стійкості Рауса: Щоб САУ була стійкою необхідно і достатньо, щоб всі коефіцієнти першого стовпця таблиці Рауса мали один і той же знак, тобто були позитивними. Якщо не всі коефіцієнти першого стовпця таблиці Рауса позитивні, тобто САУ нестійка, число правого коріння характеристичного рівняння рівне числу змін знаку в першому стовпці таблиці Рауса.

Критерій Гурвіца

Цей критерій дозволяє визначити стійкість САУ, якщо характеристичне рівняння замкнутої системи представлене у вигляді:

Для цього будується головний визначник Гурвіца за наступним правилом: по головній діагоналі виписуються всі коефіцієнти від до в порядку зростання коефіцієнтів. Стовпці вгору від головної діагоналі заповнюються коефіцієнтами характеристичного рівняння з послідовно зростаючими індексами, а стовпці вниз – коефіцієнтами з послідовно убиваючими індексами. На місці коефіцієнтів з індексами, великими порядку характеристичного рівняння і меншими нуля, проставляють нулі.

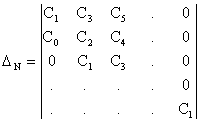
Виділяючи в головному визначнику Гурвіца діагональний мінор, отримуємо визначника Гурвіца нижчого порядку. Номер визначника Гурвіца визначається номером коефіцієнта по діагоналі, до якого складають даного визначника.

, , .

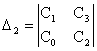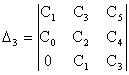Умовою даного критерію є, щоб САУ була стійка, необхідно і достатньо, щоб визначник Гурвіца і його діагональний мінор мали знаки, однакові із знаком першого коефіцієнта характеристичного рівняння замкнутої САУ. При для стійкості САУ необхідно і достатнє виконання умов:

Розглянемо замкнуту САУ, що складається з трьох послідовно включених аперіодичних ланок, охоплених 100% зворотним зв'язком.

Передавальна розімкненою САУ функція має вигляд:

Передавальна функція замкнутої САУ визначається як

Головний визначник Гурвіца має вигляд:

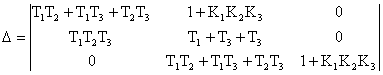Перший визначник Гурвіца . Ця умова виконується для всіх

можливих комбінацій параметрів САУ.

Другий визначник Гурвіца визначається як

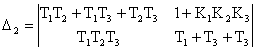Розкриваючи визначника отримуємо

Вирішуючи це рівняння щодо сумарного коефіцієнта посилення САУ, визначуваного як

отримуємо, що

З цього виходить, що сумарний коефіцієнт посилення САУ не може перевищувати деяку величину. Отже, межі зменшення погрішності стабілізації регульованої координати в такій системі обмежені. [2]

Частотний критерій Михайлова

Критерій Михайлова – це частотний критерій, що дозволяє судити про стійкість замкнутої системи по поведінці її характеристичного вектора на комплексній площині. Характеристичний вектор отримують шляхом підстановки у вираз для характеристичного полінома

Значення . Тоді характеристичний вектор представляється комплексною величиною, визначуваною як:

Де

Якщо задаватися різними значеннями і відкладати значення по горизонтальній, а – по вертикальній осям декартової системи координат, то буде отримана крива, звана годографом характеристичного вектора або годографом Михайлова. Інше формулювання: годографом Михайлова називається безліч крапок, утворених при русі характеристичного вектора САУ при зміні частоти від 0 до .

Тобто для стійкості САУ необхідне виконання умови вигляду:

Для виведення цього твердження представимо характеристичний поліном у вигляді

де – коріння характеристичного рівняння .

На комплексній площині кожному кореню відповідає певна точка. Підставивши, отримуємо

Кожен вектор може бути представлений у вигляді вектора, почало якого лежить в крапці, що визначає корінь а кінець лежить на уявній осі. Отже, можна представити сумарним вектором, рівним твору елементарних векторів. Модуль сумарного вектора буде рівний твору модулів окремих векторів, а фаза – сумі фаз цих векторів. При зміні частоти кінець кожного вектора переміщатиметься уздовж уявної осі. При зміні частоти від до кожен вектор, що становить, почало якого лежить на речовій осі, обернеться на кут, рівний, якщо його початок лежить в лівій на півплощині, і рівний –, якщо його початок лежить в правій на півплощині. Кожна пара комплексно-зв'язаного коріння – відповідно на кут +.

Якщо характеристичне рівняння має m коріння в правій на півплощині,

то в лівій на півплощині число цього коріння буде рівне n-m. При зміні частоти від до сумарний кут повороту вектора характеристичного полінома визначається як

Для стійкості САУ необхідне і достатньо, щоб все коріння характеристичного рівняння лежало в лівій на півплощині, тобто щоб . Таким чином, якщо вектор характеристичного полінома замкнутої САУ порядку "n" при зміні частоти від до описує в позитивному напрямі кут n, то така система регулювання буде стійка. Інакше САУ буде нестійка.

Через симетричність кривої, що описується кінцем вектора характеристичного полінома, можна обмежитися розглядом лише її частини, відповідної позитивним значенням частоти. При цьому кут, що описується вектором характеристичного полінома при зміні частоти від 0 до, зменшиться удвічі і визначатиметься як

алгоритм програмний слідкувальний система

Формулювання критерію: для стійкості системи необхідно і достатньо, щоб її характеристичний вектор при зміні частоти від 0 до обернувся в позитивному напрямі (проти годинникової стрілки), починаючи з позитивної речової осі на число квадрантів, рівне порядку характеристичного рівняння.

На рисунок 1.3 приведені годографи Михайлова для стійких і нестійких САУ. Зміну коефіцієнта викликає зрушення годографа Михайлова уздовж горизонтальної осі без його деформації. Це дає можливість оцінити граничне значення цього коефіцієнта, при якому зберігаються умови стійкої роботи САУ. [2]

Логарифмічний частотний критерій

Логарифмічний критерій – це частотний критерій, що дозволяє судити про стійкість замкнутої САУ по вигляду логарифмічної характеристики розімкненої системи. Цей критерій заснований на однозначному зв'язку ЛФЧХ і АФЧХ систем автоматичного управління.

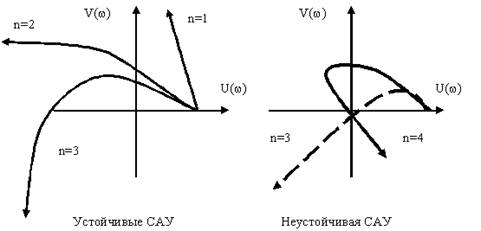
Рисунок 1.3 - Годографи Михайлова для стійких і нестійких САУ

При цьому розглядаються САУ, що базуються на використанні стійких розімкнених систем. Крім того, розглядаються системи з астатизмом не вище другого порядку.

Як випливає з критерію стійкості Найквіста в стійких САУ фазове зрушення може досягати значення тільки при модулях комплексної передавальної функції, меншому чим одиниця. Це дозволяє легко визначити стійкість по вигляду ЛАЧХ і ЛФЧХ.

Формулювання критерію: для стійкості системи в замкнутому стані необхідно і достатньо, щоб в діапазоні частот, де ЛАЧХ розімкненої системи більше нуля число переходів фазової характеристики прямої знизу верх перевищувало на число переходів зверху вниз, де а – число коріння характеристичного рівняння розімкненої системи, лежачого в правій на півплощині.

У окремому випадку для стійкої розімкненої системи (а=0) необхідною і достатньою умовою замкнутої системи є необхідність виконання наступної умови. У діапазоні частот, де, фазова частотна характеристика не повинна перетинати прямої, або перетинати її однакове число разів від низу до верху і зверху вниз.

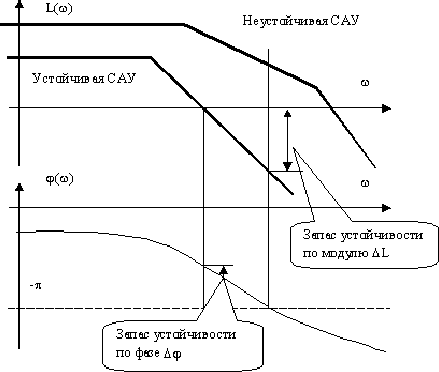
Рисунок 1.4 - ЛФЧХ стійкою і нестійкою САУ

Критичним значенням коефіцієнта перетворення називається таке його значення, при якому АФЧХ проходить через точку (-1, j0) і система знаходиться на межі стійкості.

Запасом по модулю називається величина в децибелах, на яку потрібно змінити коефіцієнт перетворення САУ, щоб привести її до межі стійкості.

де — частота, при якій фазова характеристика рівна .

Запасом стійкості по фазі називається кут, на який потрібно повернути амплітудно-фазову характеристику розімкненої системи, щоб замкнута САУ опинилася на межі стійкості.