Навигация
Пример синтеза структуры аналоговой части циклического фильтра Калмана – Бьюси
3. Пример синтеза структуры аналоговой части циклического фильтра Калмана – Бьюси
Исходными данными для синтеза схемы циклического фильтра Калмана – Бьюси (ФКБ) являются стартовая конфигурация его структурной схемы, значения коэффициентов усиления и времени функционирования на цикле ![]() .
.
Пусть необходимо производить измерения на интервале ![]() и значение скорости изменения входного сигнала на входе ФКБ не превышает
и значение скорости изменения входного сигнала на входе ФКБ не превышает ![]() , а интенсивность сигнала типа белого шума определяется значением
, а интенсивность сигнала типа белого шума определяется значением ![]() , причем
, причем ![]() . Следуя методике, изложенной в работе [4], зададим начальное значение ковариационной матрицы
. Следуя методике, изложенной в работе [4], зададим начальное значение ковариационной матрицы ![]() следующим образом:
следующим образом:
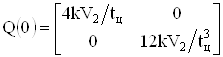 , (18)
, (18)
где ![]() – некоторый коэффициент пропорциональности. Тогда значения коэффициентов усиления [4], определяемые решениями матричного уравнения Риккати, будут иметь следующий вид:
– некоторый коэффициент пропорциональности. Тогда значения коэффициентов усиления [4], определяемые решениями матричного уравнения Риккати, будут иметь следующий вид:
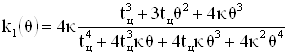 ,
(19)
,
(19)
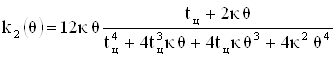 . (20)
. (20)
Дополнительные исследования показывают, что оптимальная точность фильтра достигается в случае, если функциональная зависимость этих коэффициентов для безразмерного времени q имеет вид, представленный на рис. 2.
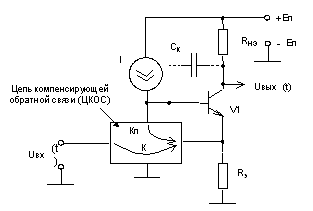
Из уравнения Риккати [2] легко синтезируется исходная принципиальная схема фильтра рис. 3. На приведенной принципиальной схеме в начальном (некомпенсированном) варианте отсутствуют операционный усилитель А9 и резисторы R13–R17, номинал резистора ![]() , а неинвертирующие входы ОУ А2, А3 и А7 соединены с землей. При указанных на схеме номиналах резисторов и конденсаторов максимальный коэффициент передачи умножающих ЦАП (ОУ А2 и А3) не превышает единицы. По формуле (7) определяем, что для
, а неинвертирующие входы ОУ А2, А3 и А7 соединены с землей. При указанных на схеме номиналах резисторов и конденсаторов максимальный коэффициент передачи умножающих ЦАП (ОУ А2 и А3) не превышает единицы. По формуле (7) определяем, что для ![]() в обоих каналах ФКБ необходимо использовать 10-разрядные ЦАП, что позволяет воспроизводить характеристики (19) и (20) в каждый момент времени с высокой точностью, то есть фактически непрерывно.
в обоих каналах ФКБ необходимо использовать 10-разрядные ЦАП, что позволяет воспроизводить характеристики (19) и (20) в каждый момент времени с высокой точностью, то есть фактически непрерывно.
Результаты численного моделирования схемы ФКБ (рис. 3) показывают, что в рассматриваемом случае достаточным является разбиение интервала времени цикла на 100 отсчетов. Таким образом, частота работы ЦАП составляет ![]() .
.
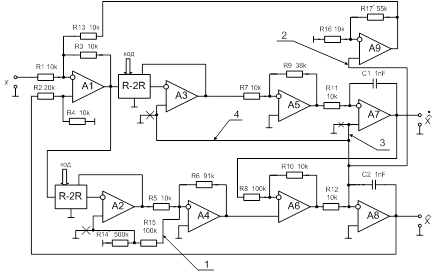
Рис. 3. Принципиальная схема гибридного циклического ФКБ 2-го порядка
Отметим, что в рассматриваемом случае каких-либо формальных строгих процедур определения допустимого интервала отклонения значений коэффициентов усиления нет. Знаменатель замороженной передаточной функции идеализированного ФКБ на ![]() -м фиксированном интервале времени следует из (6) и может быть представлен следующим образом:
-м фиксированном интервале времени следует из (6) и может быть представлен следующим образом:
![]() . (21)
. (21)
Из представленных на рис. 2 временных зависимостей коэффициентов усиления следует, что на каждом интервале времени (![]() ) указанный знаменатель является гурвицевым, так как выполняется условие
) указанный знаменатель является гурвицевым, так как выполняется условие ![]() . С учетом частотных свойств ОУ, входящих в состав реального ФКБ, и их идентичности полином (21) можно записать следующим образом:
. С учетом частотных свойств ОУ, входящих в состав реального ФКБ, и их идентичности полином (21) можно записать следующим образом:
![]() , (22)
, (22)
где ![]() .
.
В выражении (22) не учтены все члены, обратно пропорциональные произведениям площадей усиления ОУ, влияние которых на свойства реализуемого ФКБ пренебрежимо мало. Используя результат [9], условие гурвицевости полинома (22) можно представить следующим образом:
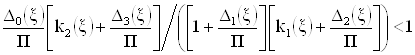 .
(23)
.
(23)
Учитывая, что ![]() , и пренебрегая членами второго порядка малости, неравенство можно записать в виде
, и пренебрегая членами второго порядка малости, неравенство можно записать в виде
![]() . (24)
. (24)
Как видно из (24), требования к минимально возможному значению площади усиления ОУ в основном определяются максимально возможным значением отношения коэффициентов усиления фильтра и могут быть снижены при компенсации (уменьшении) величины ![]() . Анализ неравенства (24) показывает, что в рассматриваемом случае условие гурвицевости полинома (22) при выполнении
. Анализ неравенства (24) показывает, что в рассматриваемом случае условие гурвицевости полинома (22) при выполнении ![]() не зависит от вариаций приращений
не зависит от вариаций приращений ![]() ,
, ![]() и
и ![]() . Поэтому дальнейший синтез схемы будем производить таким образом, чтобы обеспечить минимальное отклонение АЧХ и переходных характеристик реального фильтра от идеализированного. В этом случае допустимое (минимально возможное) значение площади усиления ОУ может быть определено из анализа отклонений временных характеристик реального фильтра от идеализированного.
. Поэтому дальнейший синтез схемы будем производить таким образом, чтобы обеспечить минимальное отклонение АЧХ и переходных характеристик реального фильтра от идеализированного. В этом случае допустимое (минимально возможное) значение площади усиления ОУ может быть определено из анализа отклонений временных характеристик реального фильтра от идеализированного.
В соответствии с предложенной методикой определим необходимые для анализа схемы наборы локальных передач ![]() ,
, ![]() ,
, ![]() и
и ![]() . Для этого по синтезированной принципиальной схеме путем сопоставления локальных передач ветвей схемы с ветвями графа обобщенной структуры определим компоненты матриц и векторов, входящих в систему, и составим блочную матрицу
. Для этого по синтезированной принципиальной схеме путем сопоставления локальных передач ветвей схемы с ветвями графа обобщенной структуры определим компоненты матриц и векторов, входящих в систему, и составим блочную матрицу ![]() , а также определим обратную
, а также определим обратную ![]() :
:
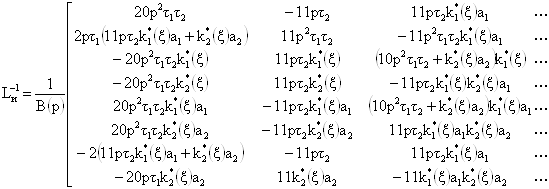
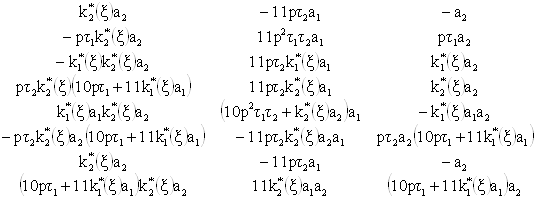
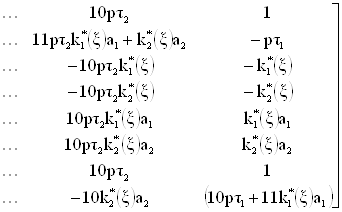 , (25)
, (25)
![]() . (26)
. (26)
нестационарный схема фильтр циклический
Из этой же матрицы легко определяется набор локальных передач ![]() ,
, ![]() ,
, ![]() и
и ![]() [4]. Результаты вычислений полиномов числителей указанных функций локальных передач схемы сведены в табл. 1. Знаменатель рассматриваемых передаточных функций определяется выражением (26).
[4]. Результаты вычислений полиномов числителей указанных функций локальных передач схемы сведены в табл. 1. Знаменатель рассматриваемых передаточных функций определяется выражением (26).
Таблица 1. Наборы локальных передач схемы ФКБ второго порядка (рис. 3)
| Вид локальной передачи | Числитель локальной передаточной функции |
| 1 | 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь верхний индекс «1» соответствует выходу ФКБ канала оценки измеряемой величины – ![]() , а индексом «2» обозначен выход ФКБ канала оценки производной измеряемой величины –
, а индексом «2» обозначен выход ФКБ канала оценки производной измеряемой величины – ![]() .
.
Используя результаты, представленные в табл. 1, по формулам и определяем приращения полиномов числителя и знаменателя передаточной функции идеализированного ФКБ:
 (27)
(27)
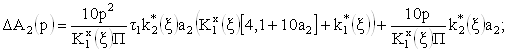
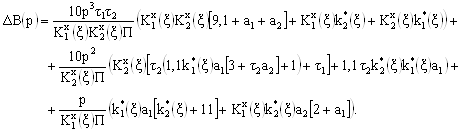 (29)
(29)
Синтез принципиальной схемы низкочувствительного ФКБ заключается во введении по определенным правилам компенсирующих контуров обратных связей, позволяющих произвести изменение значений приращений (27)–(29), с целью уменьшения активной составляющей функции чувствительности.
Примем значение частоты единичного усиления ОУ равным ![]() Гц; легко видеть, что при этом условие (24) выполняется. В качестве указан-ных активных элементов можно использовать отечественные микромощ-ные ОУ – К140УД12 (при соответствующем токе управления). По формуле (10) определяем значение верхней границы частотного диапазона ФКБ
Гц; легко видеть, что при этом условие (24) выполняется. В качестве указан-ных активных элементов можно использовать отечественные микромощ-ные ОУ – К140УД12 (при соответствующем токе управления). По формуле (10) определяем значение верхней границы частотного диапазона ФКБ ![]() . Решая оптимизационную задачу (8), определяем область из-менения параметров схемы, соответствующую «наихудшему случаю» –
. Решая оптимизационную задачу (8), определяем область из-менения параметров схемы, соответствующую «наихудшему случаю» – ![]() и
и ![]() . По результатам вычислений, представленным в табл. 1, определяем функции чувствительности передаточной функции схемы по каждому из ее выходов для каждого ОУ. Далее, решая ряд оптимизационных задач с учетом ограничений и полученной выше допустимой области вариаций параметров схемы, определяем значения модулей указанных функций чувствительности. Результаты ранжирования ОУ по степени их влияния представлены на диаграмме рис. 4.
. По результатам вычислений, представленным в табл. 1, определяем функции чувствительности передаточной функции схемы по каждому из ее выходов для каждого ОУ. Далее, решая ряд оптимизационных задач с учетом ограничений и полученной выше допустимой области вариаций параметров схемы, определяем значения модулей указанных функций чувствительности. Результаты ранжирования ОУ по степени их влияния представлены на диаграмме рис. 4.
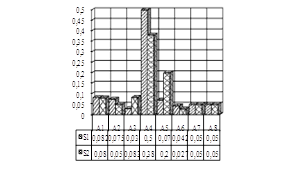
Рис. 4. Диаграмма модулей функций чувствительности ОУ
Здесь![]() – оценки модулей функций чувствительности для канала оценки измеряемой величины –
– оценки модулей функций чувствительности для канала оценки измеряемой величины – ![]() ,
, ![]() – оценки модулей функций чувствительности для канала оценки производной измеряемой величины –
– оценки модулей функций чувствительности для канала оценки производной измеряемой величины – ![]() .
.
Из приведенной на рис. 4 диаграммы видно, что наибольший вклад в качественную оценку показателей схемы вносит площадь усиления ОУ ![]() .
.
Результаты численного моделирования исходной схемы ФКБ (без дополнительных компенсирующих контуров ОС) в частотной и временной областях для указанного выше значения частоты единичного усиления ОУ представлены соответственно на рис. 5 и 6 (моделирование производилось с помощью пакета прикладных программ MicroCap. Из приведенных рисунков видно, что для принятой стартовой структуры ФКБ частотные свойства ОУ, входящих в состав реализуемого фильтра (рис. 3), оказывают достаточно большое влияние на реализуемые схемой частотные и переходные характеристики. С целью снижения влияния параметров доминирующих ОУ на характеристики в схемы вводятся дополнительные компенсирующие контуры обратных связей № 1, 2, 3 и 4 (рис. 3), позво-ляющие значительным образом снизить указанное влияние [4]. Основные результаты этапов синтеза дополнительных контуров схемы представлены в табл. 2.
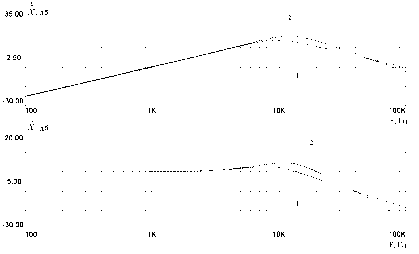
Рис. 5. АЧХ схемы ФКБ второго порядка без дополнительных контуров ОС
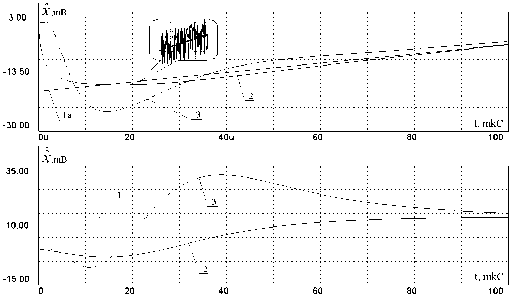
Рис. 6. Реакция схемы ФКБ второго порядка (без дополнительных контуров ОС) на линейно изменяющееся входное воздействие с заданным уровнем шума
Таблица 2. Основные результаты этапов синтеза компенсирующих контуров ОС
| Контур ОС | Поправочный член полиномов числителей и знаменателя передаточной функции ФКБ | Результат в частотной области | ||
| 1 |
| Уменьшение
| ||
| 2 |
| Уменьшение
| ||
| 3 |
| Уменьшение | ||
| 4 |
| Уменьшение
| ||
| Примечание. Здесь | ||||
Поясним методику синтеза дополнительных контуров ОС на примере построения контура № 2 (рис. 3). Из рис. 5 видно, что влияние инер-ционных свойств ОУ, входящих в состав схемы, приводит к увеличению относительного приращения коэффициента передачи и частоты среза реа-лизуемой АЧХ. Анализ диаграммы (рис. 4) и набора локальных передач ![]() , приведенного в табл. 1, показывает, что наибольший вклад при формировании указанных выше приращений вносят площади усиления ОУ А4 и А5. Путем анализа элементов строк и столбцов матрицы (25) опре-деляется необходимый вид поправочного члена для компенсации вклада указанных ОУ в качественные показатели реализуемой схемы ФКБ
, приведенного в табл. 1, показывает, что наибольший вклад при формировании указанных выше приращений вносят площади усиления ОУ А4 и А5. Путем анализа элементов строк и столбцов матрицы (25) опре-деляется необходимый вид поправочного члена для компенсации вклада указанных ОУ в качественные показатели реализуемой схемы ФКБ
![]() .
(30)
.
(30)
Для создания дополнительного узла схемы и обеспечения необходимого коэффициента усиления в схему был введен дополнительный ОУ А9 (см. рис. 3). С учетом введенной дополнительной связи и площади усиления ОУ А9 абсолютное приращение полинома знаменателя передаточной функции ФКБ определяется следующим образом:
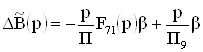 ; (31)
; (31)
![]() ;
;
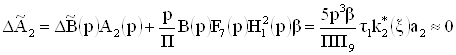 ,
,
где локальные передачи ![]() ,
, ![]() и
и ![]() определяются из табл.1.
определяются из табл.1.
Значения параметров ![]() и
и ![]() определяются в каждом конкретном случае путем решения оптимизационной задачи или моделирования схемы ФКБ в частотной и во временной областях. Аналогичным образом производится построение и других компенсирующих контуров схемы, введение которых приводит к уменьшению активной составляющей функции чувствительности.
определяются в каждом конкретном случае путем решения оптимизационной задачи или моделирования схемы ФКБ в частотной и во временной областях. Аналогичным образом производится построение и других компенсирующих контуров схемы, введение которых приводит к уменьшению активной составляющей функции чувствительности.
Результаты численного моделирования синтезированной схемы ФКБ (с введенными дополнительными компенсирующими контурами ОС), представленные на рис. 7–9, показывают высокий уровень приближения ее характеристик к соответствующим характеристикам идеализированной схемы как в частотной, так и во временной областях.
При снижении требований к точности реализации схемой ФКБ временных характеристик частота единичного усиления ОУ может быть снижена до ![]() , значение номинала сопротивления R14 в этом случае должно быть увеличено до
, значение номинала сопротивления R14 в этом случае должно быть увеличено до ![]() . Применение указанного подхода при использовании микромощных ОУ позволяет значительно снизить потребляемую от источников питания мощность. Результаты моделирования схемы ФКБ, соответствующие рассматриваемому случаю, представлены на рис. 9 и 10.
. Применение указанного подхода при использовании микромощных ОУ позволяет значительно снизить потребляемую от источников питания мощность. Результаты моделирования схемы ФКБ, соответствующие рассматриваемому случаю, представлены на рис. 9 и 10.
Следует отметить, что характеристики ФКБ во временной и частотной областях в случае применения ОУ с ![]() удается зна-чительным образом приблизить (вплоть до их практического совпадения) к соответствующим характеристикам схемы ФКБ с ОУ
удается зна-чительным образом приблизить (вплоть до их практического совпадения) к соответствующим характеристикам схемы ФКБ с ОУ ![]() при увеличении частоты единичного усиления дополнительного ОУ A9 до
при увеличении частоты единичного усиления дополнительного ОУ A9 до ![]() , требования к его статическому коэффициенту усиления при этом остаются невысокими (
, требования к его статическому коэффициенту усиления при этом остаются невысокими (![]() ).
).
Таким образом, результаты указывают на практическую осуществимость нестационарных электронных схем с высокими качественными показателями. Основные параметры схемы циклического ФКБ второго порядка при использовании различных типов отечественных ОУ с учетом определенных выше ограничений (![]() ,
,![]() ) приведены в табл. 3.
) приведены в табл. 3.
Таблица 3. Основные параметры схемы циклического ФКБ второго порядка
| Тип ОУ |
МГц |
ОУ, мА / ФКБ с доп. конт. ОС, мА | Погрешность оценивания на конец цикла, с дополнительными контурами ОС, % / без доп. конт. ОС, % | |
| канал оценки величины | канал оценки производной | |||
| К544УД2 | 15,0 | 6,0 / 54,0 | - / | - / |
| К140УД25 | 3,0 | 4,7 / 42,3 | 0,51 / 1,9 | 0,28 / 1,7 |
| К544УД1А | 1,0 | 3,5 / 31,5 | 2,2 / 7,6 | 1,1 / 6,8 |
| К140УД12* | 0,5 | 0,64 / 5,76 | 6,6 / 44,3 | 4,1 / 39,7 |
| К140УД12* | 0,2 | 0,36 / 3,24 | 18,2 / 84,5 | 16,4 / 81,2 |
| Примечание*. При соответствующем токе управления. | ||||
Из приведенной таблицы видно, что повышения точности оценивания схемой ФКБ можно достичь двумя способами. В первом случае указанного эффекта можно добиться путем увеличения частоты единичного усиления ОУ, входящих в состав схемы, однако это приведет к повышению потребляемой от источников мощности. Во втором случае указанный эффект достигается введением в схему дополнительных компенсирующих контуров ОС, что позволяет при практически неизменной потребляемой мощности получить лучшие результаты. Например, применение первого подхода, связанное с увеличением
Библиографический список
1. Ланкастер, П. Теория матриц [Текст] : пер. с англ. / П. Ланкастер. – М. : Наука, 2008. – 272 с.
2. Ланнэ, А.А. Оптимальная реализация линейных электронных цепей [Текст] / А.А. Ланнэ, Б.С. Саркисян // Радиотехника. – 2009. – Т. 34, № 7. – С. 14–20.
3. Ланнэ, А.А. Оптимальная реализация линейных электронных RLC-схем [Текст] / А.А. Ланнэ, Е.Д. Михвйлова, Б.С. Саркисян, Я.Н. Матвийчук. – Киев : Наукова думка, 2010. – 205 с.
4. Лурье, О.Б. Интегральные микросхемы в усилительных устройствах [Текст] / О.Б. Лурье. – М. : Радио и связь, 2008. – 175 с.
5. Лыпарь, Ю.И. Проектирование оптимальных структур активных RC-фильтров [Текст] / Ю.И. Лыпарь, Д.А. Скобейка // Избирательные системы с обратной связью. – 2007. – Вып. 6. – С. 141.
6. Лыпарь, Ю.И. Структурный синтез электронных цепей [Текст] / Ю.И. Лыпарь. – Л. : ЛПИ, 2008. – 84 с.
7. Максимович, Н.Г. Методы топологического анализа электрических цепей [Текст] / Н.Г. Максимович. – Львов : Изд-во Львовского ун-та, 2010. – 258 с.
8. Масленников, В.В. Избирательные RC-усилители [Текст] / В.В. Масленников, А.П. Сироткин. – М. : Энергия, 2010. – 215 с.
9. Мееров, М.В. Синтез структур систем автоматического регулирования высокой точности [Текст] / М.В. Мееров. – М. : Наука, 2007. – 423 с.
10. Немудров, В.Г. Системы на кристалле. Проектирование и развитие [Текст] / В.Г. Немудров, Г. Мартин. – М. : Техносфера, 2008. – 216 с.
11. Остапенко, А.Г. Анализ и синтез линейных радиоэлектронных цепей с помощью графов [Текст] / А.Г. Остапенко. – М. : Радио и связь, 2009. – 280 с.
12. Прокопенко, Н.Н. Архитектура и схемотехника быстродействующих операционных усилителей [Текст] / Н.Н. Прокопенко, А.С. Будяков. – Шахты : Изд-во ЮРГУЭС, 2006. – 230 с.
13. Прокопенко, Н.Н. Архитектура и схемотехника с собственной и взаимной компенсацией импедансов [Текст] / Н.Н. Прокопенко, Н.В. Ковбасюк. – Шахты : Изд-во ЮРГУЭС, 2007. – С. 325.
14. Прокопенко, Н.Н. Быстродействующий СВЧ-операционный усилитель с нелинейной токовой обратной связью [Текст] / Н.Н. Прокопенко, А.С. Будяков, Н.В. Ковбасюк // Актуальные проблемы твердотельной электроники и микроэлектроники : труды 10-й Междунар. науч. конф. и школы-семинара. – Таганрог, 2006. – Ч. 2. – С. 161–164.
15. Прокопенко, Н.Н. Нелинейная активная коррекция в прецизионных аналоговых микросхемах [Текст] / Н.Н. Прокопенко. – Ростов н/Д. : Изд-во СКНЦ ВШ, 2010. – 224 с.
16. Свирщева, Э.А. Алгоритм и программа синтеза RC-схем с операционными усилителями в дифференциальном включении [Текст] / Э.А. Свирщева, А.И. Минаев // Избирательные системы с обратной связью. – Таганрог, 2008. – Вып. 4. – С. 185–186.
17. Сигорский, В.П. Проблемная адаптация систем автоматизированного проектирования [Текст] / В.П. Сигорский // Автоматизация проектирования в электронике. – Киев : Техника, 2009. – Вып. 26. – С. 3–14.
18. Синтез активных RC-цепей. Современное состояние и проблемы [Текст] / под ред. А.А. Ланнэ. – М. : Связь, 2007. – С. 296.
19. Старченко, Е.И. Мультидифференциальные операционные усилители [Текст] / Е.И. Старченко // Проблемы современной аналоговой микросхемотехники : сборник трудов МНПС. – Шахты, 2009. – С. 35–42.
20. Тафт, В.А. Спектральные методы расчета нестационарных цепей и систем [Текст] / В.А. Тафт. – М. : Энергия, 2008. – 272 с.
21. Торговников, Р.А. Приборно-технологическое моделирование SiDe биполярных и МОП-транзисторов структур СБИС [Текст] / Р.А. Торговников // Проблемы разработки перспективных микроэлектронных систем : материалы Всерос. науч.-техн. конф. – Подмосковье, 2006. – С. 173–178.
22. Фаддеева, В.И. Вычислительные методы линейной алгебры [Текст] / В.И. Фаддеева, Д.К. Фаддеев. – М. : Физматгиз, 2009. – 655 с.
23. Филаретов, Г.А. Организация структуры критериев в задачах векторной оптимизации радиотехнических цепей и систем [Текст] / Г.А. Филаретов, Л.Б. Шустерман, Т.В. Мазюкевич // Информатика. Сер. Автоматизация проектирования. – 2009. – Вып. 3. – С. 45–54.
24. Чибизов, Д.Г. Автоматизация процедур поиска решений при структурном синтезе нестационарных ARC-схем с расширенным частотным и динамическим диапазонами [Текст] / Д.Г. Чибизов // Интеллектуальные САПР. Тем. вып. Известия ТРТУ. – 2009. – № 3. – С. 224–228.
25. Чибизов, Д.Г. Структурный синтез гибридных фильтров Калмана-Бьюси [Текст] : дис. … канд. техн. наук / Чибизов Д.Г. – Таганрог, 2009. – 202 с.
26. Штойер, Р. Многокритериальная оптимизация [Текст] / Р. Штойер. – М. : Радио и связь, 2008. – 504 с.
27. Akerberg, D. A versative RC building block with inherent compensation for the finite bandwidth of the amplifier / D. Akerberg, К. Mossberg // IEEE Trans. – 2008. – V. CAS-21. – Р. 75–78.
28. Applications handbook. Burr-Brown Corp. – 2009. – Р. 425.
29. Brackett, P. Active compensation for high frequensy effects in op-amp circuits with applications to active RC-filters / Р. Brackett, А. Sedra // IEEE Trans. – 2006. – V. CAS-23, № 2. – Р. 68–72.
Похожие работы
... постоянной времени усилителя и, следовательно, его граничной частоты определяется соотношениями (42)–(44). Завершая обсуждение найденных принципов собственной и взаимной компенсации влияния паразитных емкостей полупроводниковых компонентов, целесообразно отметить два обстоятельства, имеющих, возможно, самостоятельное значение в аналоговой микросхемотехнике. Во-первых, относительно хорошая ...
... Для уменьшения массы и габаритных размеров готового устройства выбираются планарные корпуса микросхем мА741, R01374 и вМ324. 2. Расширенное техническое задание Наименование изделия: "Эквалайзер с активными фильтрами". Эквалайзер представляет собой многополосный регуляторы тембра, позволяющий осуществлять одновременную и взаимонезависимую регулировку на нескольких частотах, предназначен для ...
... сим=()*tg(k*l)/=(7,5/π)* tg(0,837*1,875)/7,5 =8,72*10-3м; Нд несим=0,5*Нд сим=4,36*10-3 м. UД=ЕД*НД=0,0000394*4,36*10-3=1,72*10-6 В Проверено выполнение следующего условия: UДUтр1,72*10-60,21*10-6. Из этого вытекает, что радиоприёмное устройство будет уверенно принимать сигнал. Рассчитано номинальное значение отношения сигнал/шум на входе приёмника: 9(1,72*10-6/0,21*10-6)2 = ...
... коэффициенты линейного расширения материалов подложек, корпусов и вспомогательных материалов должны быть согласованы для обеспечения работы микросхем при повышенных уровнях мощности. Конструирование СВЧ микросхем включает расчет и проектирование изделия по заданным электрическим параметрам с учетом процессов сборки и регулировки. При этом определяют вариант схемы узла, материал и геометрические ...
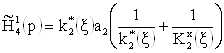 ,
,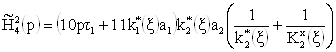 ,
,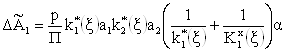 ,
,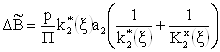 ,
,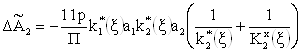 .
.

0 комментариев