Навигация
6. Сделать выводы
– какие значения массива экспериментальных данных являются случайными ошибками, и с помощью какого правила определялось наличие ошибок;
– как изменяются показатели вариации после исключения случайных ошибок;
– как изменяется доверительный интервал при изменении доверительной вероятности.
Исходные данные для выполнения задания
| Вариант | Задание |
| 1 | 8,5 7,7 8,4 7,3 8,4 8,4 8,3 7,6 8,7 8,4 8,4 6,1 6,2 7,3 8,4 8,3 7,8 8,3 7,5 2,1 11,2 18,1 8,2 8,7 9,9 Доверительные вероятности: p1 =0,85 p2 =0,95 p3 =0,995 |
| 2 | 22 24 28 22 24 24 24 33 24 25 24 25 24 24 25 27 26 24 25 25 27 12 34 Доверительные вероятности: p1 =0,8 p2 =0,9 p3 =0,99. |
| 3 | 1,3 1,2 1,2 0,9 0,9 0,8 1,2 1,1 1,2 1,5 0,3 1,2 1,3 1,2 1,2 1,2 1,1 1,2 1,2 1,1 2,1 1,2 1,3 Доверительные вероятности: p1 =0,88 p2 =0,98 p3 =0,997. |
| 4 | 40 45 44 45 35 46 47 48 43 50 45 47 38 45 44 73 41 44 40 46 44 15 43 Доверительные вероятности: p1 =0,85 p2 =0,99 p3 =0,997. |
| 5 | 2 11 10 10 9 10 11 10 9 10 10 10 11 10 9 10 11 10 10 11 10 11 19 Доверительные вероятности: p1 =0,8 p2 =0,85 p3 =0,95. |
| 6 | 8,5 8,3 8,4 8,4 8,4 8,4 8,3 8,5 8,6 8,4 1,8 8,4 8,4 7,4 6,2 8,4 8,4 8,3 14,7 8,3 8,3 8,4 8,3 Доверительные вероятности: p1 =0,95 p2 =0,99 p3 =0,997. |
| 7 | 8,5 7,7 8,4 1,1 8,4 8,3 7,6 8,7 8,4 7,2 8,4 8,4 6,1 14,5 8,4 8,4 8,3 7,8 8,3 7,5 8,3 7,7 8,8 Доверительные вероятности: p1 =0,86 p2 =0,95 p3 =0,995. |
| 8 | 8,5 4,2 8,4 8,3 8,4 8,4 8,3 8,6 8,7 8,4 8,2 8,4 8,4 12,3 9,2 8,3 8,4 8,3 8,4 8,3 8,8 8,8 8,5 8,9 Доверительные вероятности: p1 =0,85 p2 =0,99 p3 =0,997. |
| 9 | 12,5 12,8 13,3 12,8 12,7 13,1 12,6 12,9 13 13,8 14,6 12,9 13 13,1 13,3 12,9 13,3 11,4 12,8 2,1 12,2 22,4 13,3 7,8 Доверительные вероятности: p1 =0,95 p2 =0,99 p3 =0,997. |
| 10 | 22 24 22 29 24 24 24 24 41 24 25 24 25 24 25 24 25 22 26 24 25 25 8 24 Доверительные вероятности: p1 =0,8 p2 =0,85 p3 =0,9. |
| 11 | 1,3 1,2 1,1 1,3 1,3 2,4 1,2 1,3 1,2 1,4 0,1 1,2 1,3 1,1 1,2 1,1 1,2 1,3 1,2 1,2 1,2 1,3 1,2 1,2 Доверительные вероятности: p1 =0,83 p2 =0,88 p3 =0,92. |
| 12 | 2,3 2,2 2,1 2,2 3,8 1,8 2,20 2,2 2,2 2,3 0,8 2,2 2,3 2,2 2,3 2,2 2,3 2,2 2,4 2,5 2,5 2,2 2,3 2,8 Доверительные вероятности: p1 =0,8 p2 =0,9 p3 =0,99. |
| 13 | 5,3 5,2 5 5,1 4,8 8,8 5,20 5,5 5,2 5,3 5,2 5,5 5,1 5,2 5,3 5,2 2,1 5,5 5,2 5,2 5,5 5,5 5,2 5,3 Доверительные вероятности: p1 =0,9 p2 =0,99 p3 =0,997. |
| 14 | 10,3 10,2 13,3 10,9 10,9 10,8 10,20 10,1 10,2 10,5 10,2 10,3 10,2 10,2 10,1 10,2 10,2 10,1 10,1 10,2 10,3 7,1 10,4 Доверительные вероятности: p1 =0,8 p2 =0,92 p3 =0,98. |
| 15 | 23 25 26 21 24 25 23,00 35 24 25 24 25 24 22 25 27 26 22 25 25 21 23 27 11 26 22 Доверительные вероятности: p1 =0,83 p2 =0,88 p3 =0,99. |
| 16 | 11 12 10 12 10 11 13 22 12 11 14 11 11 13 11 13 14 13 12 10 12 11 12 11 2 17 12 Доверительные вероятности: p1 =0,85 p2 =0,91 p3 =0,98. |
| 17 | 12 13,8 13,1 11,8 10,7 11,1 12,20 12,1 13,6 12,8 21,1 10,9 13,1 13,3 13,8 11,9 13,3 3,5 11,1 12,3 11 11,3 12,1 11,9 Доверительные вероятности: p1 =0,82 p2 =0,9 p3 =0,96. |
| 18 | 2,1 2,3 2 2,2 2,5 2,3 2,10 2,3 2,2 2,1 2,3 5,2 2,5 2,1 2,1 2,2 2,2 2,2 2,2 2,2 1,9 5,1 2,1 2,3 Доверительные вероятности: p1 =0,81 p2 =0,91 p3 =0,997. |
| 19 | 1,1 1,3 1,2 0,95 0,99 1,3 1,10 1,4 1,1 1,7 0,1 1,5 1,2 1,2 1,1 1,2 1,3 1,2 1,2 1,1 1,15 1,2 1,5 2,2 Доверительные вероятности: p1 =0,89 p2 =0,95 p3 =0,97. |
| 20 | 22,5 22,8 23,3 22,8 22,7 11,5 22,60 22,9 23,1 23,8 24,6 22,9 23 23,1 22,9 23,3 35,5 23,1 25,5 27,1 23,1 22,1 22,3 23,3 Доверительные вероятности: p1 =0,92 p2 =0,98 p3 =0,995. |
Похожие работы
... видно, с ростом числа измерений различие между результатами, вычислениями по распределению Стьюдента и по нормальному распределению уменьшается. Контрольные вопросы 1. Цель математической обработки результатов эксперимента; 2. Виды измерений; 3. Типы ошибок измерения; 4. Свойства случайных ошибок; 5. Почему среднеарифметическое значение случайной величины при нормальном законе ее ...
... Как видно, с ростом числа измерений различие между результатами, вычислениями по распределению Стьюдента и по нормальному распределению уменьшается. Контрольные вопросы Цель математической обработки результатов эксперимента; Виды измерений; Типы ошибок измерения; Свойства случайных ошибок; Почему среднеарифметическое значение случайной величины при нормальном законе ее распределения является ...
... с ценой деления 1 сек. Области применения: построение геодезических сетей сгущения (триангуляция 4 класса, полигонометрия IV класса), в прикладной геодезии (строительство, изыскания и т.д.), астрономо- геодезических измерениях (определение азимута по Солнцу и по Полярной Звезде). Модель 3Т5КП предназначена для измерения горизонтальных и вертикальных углов и не имеет микрометра. Области ...
... у возводимого в степень числа. 4. В промежуточных результатах брать на одну десятичную цифру больше, чем по правилам округления, а для оценки порядка вычислений округлять все числа до первой значащей. Математическая обработка результатов анализа На любом из перечисленных этапов количественного анализа могут быть допущены и, как правило, допускаются погрешности, поэтому, чем меньшее число ...
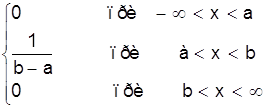
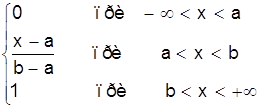
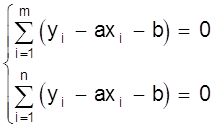
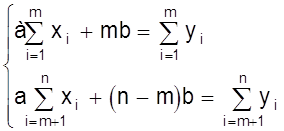
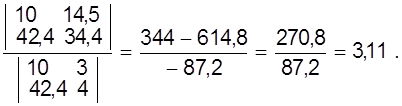
0 комментариев