Исследование влияния прямоугольного проводящего экрана на ТВ передающую антенну с режекторной ДН

Исследование влияния прямоугольного проводящего экрана на ТВ передающую антенну с режекторной ДН

1. Постановка задачи

В настоящее время происходит интенсивное развитие сети телевизионного и УКВ ЧМ радиовещания. Сети ТВ-ретрансляторов планируются для расширения зоны действия мощных РПС, расположенных в краевых административных и культурных центрах. Развитие сети осуществляется в основном за счет увеличения числа станций малой мощности, особенно в зоне действия спутниковых систем, внедрения систем коллективного приема и кабельного телевидения, освоения диапазона дециметровых волн.

Расширение сети радиовещания на метровых и дециметровых волнах требует разрешения таких сложных вопросов, как определение зон обслуживания станций и зон помех на пересеченной и гористой местности, а также обеспечения ЭМС между радиопередающими станциями вещательной службы, между службами ТВ и ОВЧ ЧМ вещания (УКВ ЧМ) и другими службами, совместно использующими общие частотные полосы. Некоторые спутниковые системы, например «Экран», работают в полосах частот, используемых для наземного ТВ вещания. Мешающее влияние других радиостанций всегда уменьшает зону обслуживания. Измерить в месте приема уровень помех от других радиостанций практически невозможно. Использование ретрансляторов не гарантирует высокого качества вещания, так как при протяженной трассе в связи с малой напряженностью поля при приеме увеличивается вероятность воздействия помех тропосферного и ионосферного распространения сигналов. [2]

Одновременно с увеличением территории, обеспечиваемой ТВ и ОВЧ ЧМ вещанием, растет число каналов транслируемых в одном пункте. Таким образом, появляется значительная потребность в антенно-фидерных устройствах для новых радиоканалов. Для уплотнения радиоканалов и учитывая электромагнитную обстановку в регионах будем использовать электромагнитные экраны.

Антенны 55 телевизионного канала (ТВК) – это антенны дециметрового диапазона, этот канал входит в V частотный диапазон, занимающий полосу частот 582 – 790 МГц. В отличие от метрового диапазона он обусловлен уменьшением элементов антенн, в связи с уменьшением длины волны. Поэтому панели антенн дециметрового диапазона целесообразно выполнять с числом вибраторов более одного, объединяя их конструктивно в этажи.

Обычно антенно-фидерные устройства (АФУ) данного диапазона располагаются на верхней площадке, на опорах или мачтах высотой около 180 м. Как правило, это верхняя площадка на тонкой опоре. [1]

В связи с наличием сложной электромагнитной обстановки в диапазоне 742,0-750,0 МГц (55 канала) возникает проблема электромагнитной совместимости радиоэлектронных средств, а именно - различных ТВ передатчиков, Чтобы гарантировать допустимое качество приема у населения, проживающего в зоне обслуживания. Телевизионные передатчики обеспечивают широкий сектор покрытия. Поэтому, исходя из реальной электромагнитной обстановки, сектор работы ТВ-антенн отличается от желаемого наличием секторов, где излучение подавляется. Так, например, применение передающих антенн с диаграммой направленности (ДН) излучения 180° позволяет вдвое увеличить значение мощности в нужном направлении.

Основной критерий подавления излучения от мешающих радиоэлектронных средств - это снижение на 10 дБ в секторе около 30 градусов. Коэффициент усиления без экрана – 5 дБ. [3]

Допускаемая нормативами неравномерность реальной ДН в зависимости от азимута излучения может достигать 3 дБ, что эквивалентно изменению излучаемой мощности вдвое и соответственно приводит к искажению идеального вида ДН.

Затенение участка зоны обслуживания при угле излучения ц° (угол, образованный горизонтальной плоскостью, проведенной через центр передающей антенны и направлением на точку приема) может быть существенно для гористой местности при решении проблем ЭМС.

Для решения поставленной задачи воспользуемся электромагнитным экраном с отверстием. Основное достоинство антенны с экраном это не только в регулирование диаграммы направленности антенны, но и в том, что благодаря наличию экрана антенна практически не возбуждаются металлоконструкцией опоры и допускает большие варианты размещения на опоре. [2]

Поскольку антенны исследуемого диапазона ТВ антенн располагаются на верхних этажах опоры, благодаря малости электрических расстояний, а также наличию экрана интерференция излучаемых волн проявляется слабо и неравномерность круговой диаграммы направленности оказывается малой.

ДН ТВ антенны с экраном рассчитаны на основе решения электродинамической задачи методом интегрального уравнения.

 

2. Алгоритм численного решения

Расчет параметров антенн выполнялся на основе предварительного решения электродинамической задачи о распределении тока по излучающим элементам методом интегрального уравнения (ИУ). Ниже приводится краткое описание использованного метода.

Электродинамическая задача решается в так называемом тонкопроволочном приближении [1.2, 1.5, 1.6]. Исследуемая антенна представляется системой электрически тонких проводников круглого сечения (сплошные поверхности аппроксимируются сетками таких проводников), которые считаются идеально проводящими, и задача формулируется следующим образом: требуется найти такое распределение тока, при котором на поверхности проводников выполняется граничное условие для электрического поля - равенство нулю тангенциальной составляющей [1.5, 1.6]. При этом в рамках тонкопроволочного приближения учитываются только продольные (параллельные оси провода) составляющие электрического поля и тока, причем последний считается нитевидным (линейным), текущим по оси провода.

Введем контур L' (необязательно гладкий и непрерывный), представляющий собой совокупность осей проводников. На этом контуре определим скалярную токовую функцию I(l') (l' - координата, отсчитываемая вдоль L').

Электрическое поле, создаваемое током I(l'), полностью определяется векторным А и скалярным f электрическими потенциалами [П.2.1]:

У = -оцФ - пкфв цю (П2ю1)

Электрические потенциалы в однородной среде (ток I(l') считается излучающим в свободном пространстве [1.5]) удовлетворяют неоднородным уравнениям Гельмгольца [П.2.1], решения которых в данном случае могут быть записаны в виде:

A(v) = m_a ò l' + I(l') G(v,v') dl' , (П2.2)

^L'

j(v) = - (jwea)^-1 ò {dI(l') / dI'} G(v,v') dl', (П2.3)

^L

где G(v,v') - ехр(-jb |v - v'|) / {|v -v'|} - функция Грина, используемая при интегрировании уравнений Гельмгольца;

v и v' - радиус-векторы точки наблюдения (в которой вычисляются потенциалы) и переменной интегрирования l', соответственно;

l' - единичный вектор, касательный к L' в точке v' (направление вектора соответствует положительному направлению L');

b = 2p/l - волновое число;

l - длина волны, м.

В (П2.3) учтен закон сохранения заряда в случае линейного тока:

jwr(l') = - dI(l')/dl'

(здесь - r(l') - погонная плотность заряда на контуре L').

Подстановка (П2.2, П2.3) в (П2.1) приводит к интегральному выражению для электрического поля, создаваемого током I(l'). Учитывая только продольную составляющую тангенциального электрического поля на поверхности проводников, введем контур L, который представляет собой контур L', перенесенный на поверхность проводников. На контуре L определим скалярные функции E_e(1) и E_t(1) - продольные составляющие тангенциальных электрических полей, создаваемых сторонними источниками (возбуждающими антенну) и током I(l'), соответственно (I - координата, отсчитываемая вдоль L). В дальнейшем под v будем подразумевать радиус-векторы точек L, соответствующих конкретным значениям l (при этом G(v,v') = G(l,l')).

С учетом введенных обозначений окончательно получим интегральное уравнение, имеющее смысл граничного условия

Е_е(1)= - Е_t(1)

для электрического поля на поверхности идеального проводника (в тонкопроволочном приближении):

оwm_ф (дбд_к) вП(к) вШ(дэ)

У_у(Ш)= òх -------- (1бд) П(к) Ш(дэ) + --------- -------- --------- ъ вдэ (П2ю4)

^Дэ 4p 4pоwe_ф вк вдэ

где к = /м - мэ/ - вспомогательная координата, отсчитываемая вдоль прямой, соединяющей точки v и v';

l_r - единичный вектор - орт оси, вдоль которой отсчитывается координата г (положительное направление - от v' к v).

Правая часть ИУ (П2.4) имеет смысл функции -E_t(l) - взятого с обратным знаком тангенциального поля, создаваемого током I(1'). Производная по r в (П2.4) соответствует градиенту в (П2.1). Круглыми скобками в (П2.4) обозначены скалярные произведения векторов (это обозначение используется и в дальнейшем).

ИУ (П2.4) в литературе иногда называют уравнением Харрингтона [1.5]. Аналогичным образом может быть получено известное уравнение Поклиигтона (при этом потенциал j из (2.1) исключается посредством условия лоренцевой калибровки потенциалов [П.2.1]).

Для решения ИУ использован широко распространенный метод моментов [1.5, 1.6], в рамках которого токовая функция для антенной решетки, состоящей из N излучателей, находится в виде разложения по базису линейно-независимых функций:

_N

I(l') = S I_k b_k (l'), (П2.5)

^K=1

N - число базисных функций;

b₁(l'), b₂(l'),... b_NM(l') - базисные функции;

I₁, I₂,... I_NM - неизвестные (искомые) коэффициенты.

Граничные условия на поверхности проводников накладываются посредством определенных на контуре L линейно-независимых весовых функций W₁(l), W₂(l), ... W_NM(l), образующих базис разложения полного тангенциального поля Е_e(l) + E_t(l), т.е. невязки приближенного решения ИУ. При этом задача о нахождении токовой функции, удовлетворяющей ИУ (П2.4), сводится к решению системы линейных алгебраических уравнений (СЛАУ):

_N(П2.6)

S Z_ik I_k = E_i , i = 1, 2, … N ,

^k=l

где коэффициенты Z_ik образуют так называемую матрицу импедансов и вычисляются по формуле:

(дбд_к) вП(к) ви_л(дэ)

Z_шл = о30 ò Ц_ш(д) ò х (1бдэ) в П(к) и_л(дэ) --------- -------- --------- ъ (П2ю7)

Дэ Дэ ввк вдэ

свободные члены СЛАУ E_i - по формуле:

E_i = ò W_i(l) E_e (l) dl . (П2.7)

L'

Что касается функции распределения стороннего поля Е_e(1), обусловливающей свободные члены СЛАУ E₁, E₂,... E_N, то способ ее определения зависит от используемой модели возбуждения (формализации сторонних источников [П.2.1]). В данном случае использована известная модель возбуждения типа "дельта-генератор", в рамках которой функция Е_e(1) = 0 всюду, за исключением зазоров активных вибраторов, к которым подведено питающее напряжением (в этих зазорах стороннее поле соответствует нормированным комплексным амплитудам питающих напряжений).

В качестве базисных использованы кусочно-синусоидальные функции, позволяющие использовать замкнутые выражения для вычисления поля в точке [1.5, 1.6] (при этом в (П2.7) исчезает интеграл по l'). Базисные функции данного типа определяются следующим образом. Контур L' разбивается на частично перекрывающиеся электрически короткие отрезки (сегменты) L'₁, L'₂, ... L'_N. Центральные точки сегментов - значения l'₁, l'₂, ... l'_N координаты l' (подстрочный индекс соответствует номеру сегмента). Начало k-го сегмента совпадает с центром предыдущего (l'_k-1), конец - с центром следующего (l'_к+1). Некоторая k-я кусочно-синусоидальная базисная функция b_k(l') отлична от нуля в пределах k-го сегмента, максимальна в его центре и убывает по синусоидальному закону до нуля при перемещении к его крайним точкам.

Сегмент, в сущности, представляет собой короткий вибратор, плечи которого могут иметь разную длину и не лежать на одной прямой ("уголковый" сегмент). Гальванические контакты между проводами (в узлах разветвления) описываются посредством сегментов, центры которых совпадают с точками контактов, а плечи расположены на разных проводах (нетрудно убедиться, что при этом автоматически выполняется закон Кирхгофа для узла цепи).

Для определения весовых функций контур L аналогичным образом разбивается на сегменты L₁, L₂, ... L_N, причем каждый сегмент L_k соответствует сегменту L'_k и находится на кратчайшем от него расстоянии. В качестве весовых использованы функции двух типов (в разных задачах):

- кусочно-синусоидальные, равные соответствующим базисным

Ц_л(д) = и_л(дэ)б д -Ю дэж

- дельта-функций Дирака

W_k(l) = 8(l-l_k).

Разновидность метода моментов при выборе весовых функций первого типа называют методом Галеркина [1.5, 1.6], при выборе весовых функций второго типа - методом сшивания в дискретных точках.

Метод Галеркина обеспечивает сравнительно быструю сходимость решения [1.5, 1.6]. Решение, получаемое методом сшивания в точках (его физическая сущность заключается в наложении граничных условий в отдельных точках контура L - точках сшивания), сходится медленнее, однако, данный метод обеспечивает наименьшие затраты машинного времени на расчет Z_ik, поскольку в силу известного свойства дельта-функции в (П2.7) исчезает интеграл по 1. Как показывает практика в зависимости от характера задачи следует использовать как метод Галеркина, так и метод сшивания.

Решением СЛАУ (П2.6) находятся коэффициенты I₁, I₂, ... I_N, которые совместно с базисными функциями аппроксимируют истинное распределение тока.

По найденному распределению тока вычисляются значения ненормированной ДН как величины, совпадающие с точностью до постоянного множителя с напряженностями поля в дальней зоне, являющегося суперпозицией полей, создаваемых отдельными сегментами (каждый сегмент рассматривается как элементарный вибратор) по формуле:

 

_N

f(и,ц) = S I_k L_k f_k (и,ц) exp [j в (r_k , 1_ИЗ)] , (П2.8)

^k=l

где и и ц - углы, определяющие направление на точку наблюдения (и - полярное расстояние, ц - азимут в сферической системе координат);

L_k - длина k-гo сегмента, м;

f_k (и,ц) - векторная (т.е. учитывающая ориентацию сегмента) диаграмма направленности элементарного вибратора, образованного k-м сегментом;

r _k - радиус-вектор центра k-rо сегмента;

1_ИЗ - единичный вектор направления на точку наблюдения (в сферической системе координат).

При исследовании многоэтажных антенн электродинамическим методом находилась ДН одного этажа. ДН антенны в горизонтальной плоскости будет, очевидно, такой же, ненормированная ДН в вертикальной плоскости вычислялась по формуле:

_L

F_ВП(и,ц) = S A_k f_эт (и) exp (j p H_k cosи), (П2.12)

^k=l

где

L - число этажей;

А_к - комплексная амплитуда возбуждения k-гo этажа;

H_k - высота k-гo этажа относительно условного центра антенны.

радиовещание антенна прямоугольный экран

 

3. Анализ влияния прямоугольного проводящего экрана на ТВ передающую антенну

3.1 ТВ антенна 5 телевизионного канала без корректировки диаграммы направленности

Рассмотрим антенну ТВК, представленную на Рис. 5.1.

Рис. 1.1 Общий вид ТВ антенны 5 ТВК

Антенна представлена в виде трех пар электрических вибраторов, расположенных на расстоянии л/4 (0,1 м) друг от друга. Пара вибраторов имеет одинаковое значение токов с фазой равной 0 и 90 градусов.

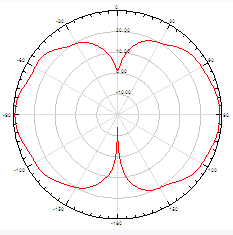
Рис. 1.2 Двухмерная диаграмма направленности для телевизионной антенны без экрана на частоте 742 МГц

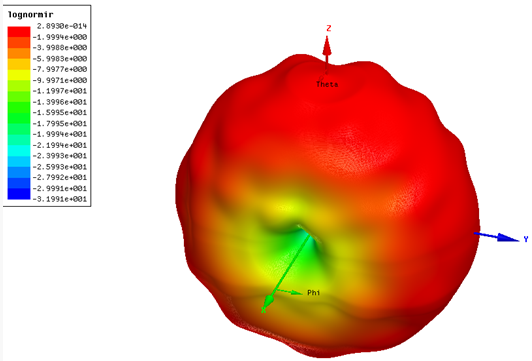
Рис. 1.3 Трехмерная диаграмма направленности для телевизионной антенны без экрана на частоте 742 МГц