Навигация
Экспертов сообщили следующие оценки из отрезка [40,100] 65, 90, 45, 80, 75, 90
6 экспертов сообщили следующие оценки из отрезка [40,100] 65, 90, 45, 80, 75, 90.
Определить решение Центра в соответствии с открытого управления.
Решение:
Вычисляют n чисел по формуле:
![]() (9)
(9)
![]()
v1=90; v2=90-10=80; v3=90-20=70; v4=90-30=60; v5=90-40=50; v6=90-50=40;
х 45 65 75 80 90 90
v 90 80 70 60 50 40
min 45 65 70 60 50 40
В качестве итогового решения берется максимальное число в последней строке: х* = 70.
Таким образом, решение Центра следующее: 70.
Задача 7
В 2003 г. в отрасли функционируют 128 фирм одинакового размера, мощностью 1000 ед. продукции в год каждая. Исследования показали, что любая фирма с вероятностью 0,5 может сохранить свой размер, с вероятностью 0,25 может увеличить размер коэффициентом пропорциональности 2,5 и с вероятностью 0,25 может уменьшить размер с коэффициентом пропорциональности 0,4.
1) Рассчитать распределение фирм по размеру в 2004 и 2005 г. в соответствии с процессом Жибера.
2) Проанализировать изменение уровня концентрации в отрасли.
Решение:
160 ед. - 400 ед. - 1000 ед. - 2500 ед. - 6250 ед.
![]() 2003г.
2003г.
 |  | ||||
![]()
![]()


![]()
![]() 2004г.
2004г.





![]()
![]()
![]() 8 ф. 16 ф. 8 ф. 16 ф. 32 ф. 16 ф. 8 ф. 16 ф. 8 ф.
8 ф. 16 ф. 8 ф. 16 ф. 32 ф. 16 ф. 8 ф. 16 ф. 8 ф.
2005г
Коэффициент концентрации:
![]() (10)
(10)
где n – число продавцов на рынке.
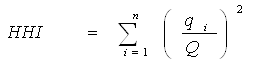 (11)
(11)
где: n – число продавцов на рынке;
qi – объем продаж i – фирмы.
1) ![]() t=2003 г.
t=2003 г.
Q3=128∙1000=128000
![]()
2) ![]() t=2004 г.
t=2004 г.
Q4=32∙400+64∙1000+32∙2500=156800
![]()
3) ![]() t=2005 г.
t=2005 г.
![]() Q5=8∙160+32∙400+48∙1000+32∙2500+8∙6250=192080
Q5=8∙160+32∙400+48∙1000+32∙2500+8∙6250=192080
У3=У4=У5
HHI3=HHI4=HHI5
Вывод: с увеличением времени, уровень концентрации в отрасли увеличился, так как в каждый следующий момент времени, увеличивается неравномерное распределение рыночных долей фирм.
Данная модель отражает стохастический подход к изменению уровня концентрации в отрасли. Данный подход делает упор на распределение рыночных долей фирмы.
Существует детерминистический подход, который делает упор на изменение количества фирм в отрасли, что в данный задаче не актуально. На практике нужно учитывать оба подхода в комплексе.
Задача 8
В сервисный центр по ремонту компьютерной техники ежемесячно поступает 300 серверов. Среднеожидаемое время ремонта (обслуживания) Тоб = 10 суток. Среднеожидаемая продолжительность времени между ремонтами Ттр = 0,1 суток. Необходимо рассчитать математическое ожидание числа серверов, ремонтируемых в месяц (в соответствии с законом Пуассона).
Решение: в соответствии с законом Пуассона математическое ожидание числа серверов, ремонтируемых в месяц равно:
М = l × t,(12)
где l – интенсивность ремонта серверов в сутки;
t – время, выбранное для определения математического ожидания (30 дней).
l = 300/ 10,1 = 29,7 сервера в сутки
М = 29,7 × 30 = 891 сервер в месяц.
Ответ: математическое ожидание числа серверов, ремонтируемых в месяц (в соответствии с законом Пуассона) равно 891 серверу.
Задача 9
Среднеожидаемое время безотказной работы (т. е. время между отказами – требованиями на обслуживание) составляет:
1. Для дешевого ненадёжного типа оборудования Ттр = 10 часов
2. Для дорогого надёжного типа оборудования Ттр = 100 часов
Среднеожидаемое время обслуживания (ремонта в случае выхода из строя) обоих видов оборудования равно Тоб = 2 часа.
Стоимость одной единицы дорогого типа оборудования – 172 000 руб., дешёвого – 10 000 руб. стоимость одного часа простоя системы – 1000 руб. определить, какой тип оборудования экономически целесообразно предпочесть в расчёте на 1000 часов работы (в соответствии с теорией массового обслуживания).
Решение: Интенсивность периодов «работа – ремонт» для ненадёжного типа оборудования составляет:
λ = 1000/12 ≈ 83,3 периода
для надёжного типа оборудования:
λ = 1000/102 ≈ 9,8 периода
Таким образом, стоимость эксплуатации ненадёжного оборудования составит: 10 000 + 83,3×2000 = 176 600 руб.
стоимость эксплуатации надёжного оборудования составит: 172 000 + 9,8×2000 = 191 600 руб.
Ответ: экономически целесообразно предпочесть более дешёвый тип оборудования.
Задача 10
Магазин «Молоко» продаёт молочные продукты. Директор магазина должен определить, сколько контейнеров сметаны следует закупить у производителя для торговли в течение недели. Вероятность того, что спрос на сметану в течение недели будет 7, 8, 9 или 10 контейнеров, равны соответственно 0,2; 0,2; 0,5; 0,1. Покупка одного контейнера сметаны обходится магазину в 700 руб., а продаётся по цене 1100 руб. Если сметана не продаётся в течение недели, она портится, и магазин несёт убытки. Сколько контейнеров сметаны желательно приобретать для продажи? Какова ожидаемая стоимостная ценность этого решения?
Решение:
7 0,2
8 0,2
9 0,5
10 0,1
К=(7·0,2+8·0,2+9·0,5+10·0,1)/(0,2+0,2+0,5+0,1)≈9 контейнеров сметаны желательно приобретать для продажи.
Значения математического ожидания или ожидаемой ценности альтернатив определяется по формуле:
EVi = ∑ pjЧVij , где(13)
EVi – ожидаемая ценность (ожидаемый доход) для i-й альтернативы
Pj – вероятность наступления j-го состояния внешней среды
Vij – ценность исхода, получаемого про выборе i-й альтернативы и наступлении j-го состояния внешней среды
Vij = 110-700=400 руб.
EVi = 7·0,2·400+8·0,2·400+9·0,5·400+10·0,1·400=560+640+1800+400=3400 руб.
ожидаемая стоимостная ценность этого решения.
Похожие работы
... и организационные меры. 6. Ресурсное обеспечение сделки. 7. Эффективность сделки (проекта). ГЛАВА 2. ОСНОВЫ ПРОГНОЗИРОВАНИЯ И ПЛАНИРОВАНИЯ НАРОДНОГО ХОЗЯЙСТВА В СОВРЕМЕННЫХ УСЛОВИЯХ 2.1. Сущность экономического прогнозирования и планирования Прогнозирование — разработка прогнозов, это специальное научное исследование конкретных перспектив развития каких либо явлений. ...
... внешнеэкономической деятельности. Балансы применяются также для выявления диспропорций в текущем периоде, вскрытия неиспользованных резервов и обоснования новых пропорций. Система балансов, используемых в прогнозировании и планировании, включает: материальные, трудовые и финансовые. В каждую из указанных групп входит ряд балансов. 2.6 Нормативный метод Нормативный метод является одним из ...
... их вклад в общественное развитие. Важными задачами, которые обычно ставятся перед исполнителями при прогнозировании и планировании, разработке соответствующей концепции, программы, мероприятия, является сохранение и развитие высокоэффективной структуры экономики, достаточного уровня доходов и социальной защищенности населения, поддержание имеющихся и налаживание новых многообразных экономических ...
... видам их деградации. 3.2 Землеустройство как основной инструмент государственной земельной политики Землеустройство включает в себя мероприятия по изучению состояния земель, планированию и организации рационального использования земель и их охраны, образованию новых и упорядочению существующих объектов землеустройства и установлению их границ на местности (территориальное землеустройство), ...
0 комментариев