Задание 1.1
Вычислить значение функции y(x) на промежутке [1;2.8] с шагом h=0.3.
![]()
В Pascal:
program z1;
uses crt;
var Xn,Xk,X,Y,H,Z:REAL;
begin
clrscr;
write('‚Enter Xn,Xk,H=');
readln(Xn,Xk,H);
X:=Xn;
repeat
z:= 1-exp((0.5)*x);
if z=0 then writeln('NO') else
Y:=ln(6.8*sqrt(x))*(exp((1/3)*(ln(abs(Z))))*(abs(Z)/Z));
writeln('X=',X:6:1,' Y=',Y:8:3);
X:=X+H;
until X>=Xk+H/2;
readkey;
end.
Результаты вычислений:
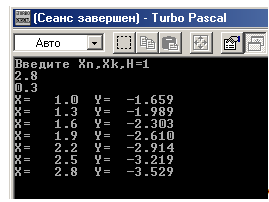
В Excel:
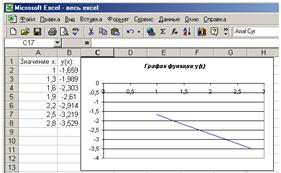
В MathCAD:
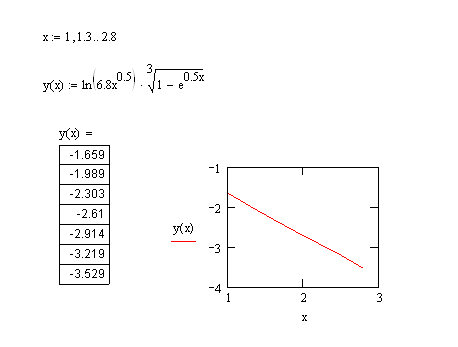
В Delphi:
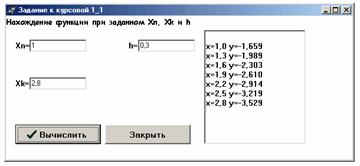
var
i:integer;
s,Xn,z,F,h,Xk:real;
procedure TForm1.BitBtn1Click(Sender: TObject);
begin
Xn:=strtoFloat(edit1.text);
h:=strtoFloat(edit2.text);
Xk:=strtoFloat(edit3.text);
repeat
z:= 1-exp((0.5)*Xn);
F:=ln(6.8*sqrt(Xn))*(exp((1/3)*(ln(abs(Z))))*(abs(Z)/Z));
Memo1.Lines.Add('x='+FormatFloat('0.0',xn)+' y='+FormatFloat('0.000',F));
Xn:=Xn+h;
until Xn>Xk;
end;
procedure TForm1.BitBtn2Click(Sender: TObject);
begin
form1.close;
end;
end.
Вывод: т.к. ответы в Pascal,Excel,MathCAD и Delphi сошлись – решение верно.
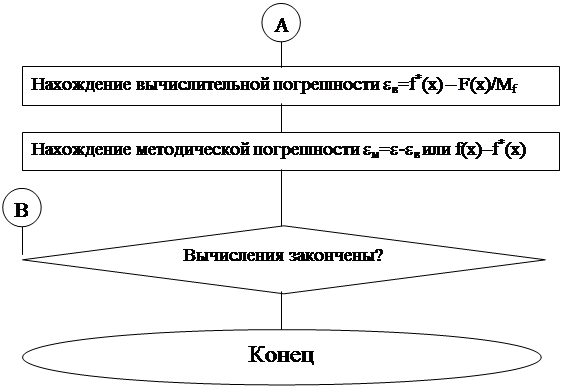
Блок-схема алгоритма решения задания №1.1
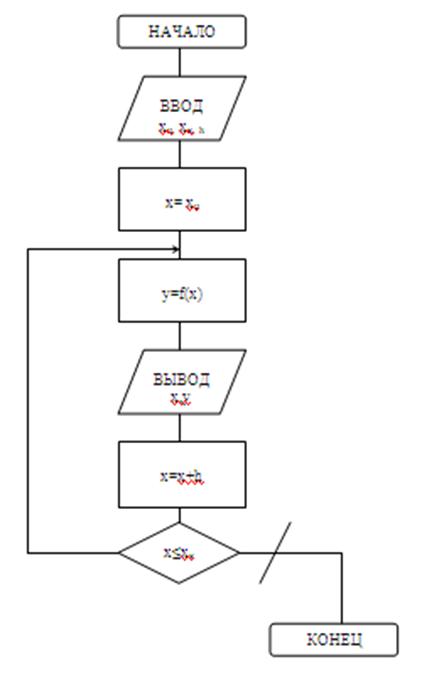
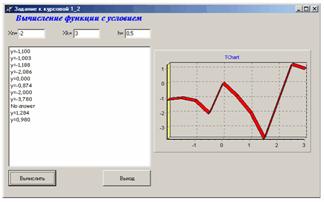
Задание 1.2
Вычислить значение функции y(x) с условием на промежутке [-2;3] с шагом h=0.5

В Pascal:
program z2;
uses crt;
label 20;
var x,y,Xn,Xk,h:real;
begin clrscr;
writeln('Please ENTER Xn,Xk,h=');
readln(Xn,Xk,h);
x:=Xn;
while x<=Xk+h/2 do
begin
if x<0 then y:=1/sin(x) else
if (x>=0) and (x<2) then y:=(2*x)/((abs(x-2)/(x-2))*(exp(1/3*(ln(abs(x-2)))))) else
if x>2 then y:=sqr(cos(x))/(x-2)
else
begin
writeln('NO answer');
goto 20;
end;
writeln('x=',x:3:1,' y=',y:6:3);
20: x:=x+h;
end;
readkey;
end.
Результаты вычислений:
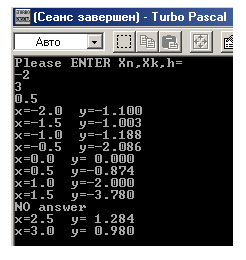
компьютерный вычисление функция алгоритм
В Excel:
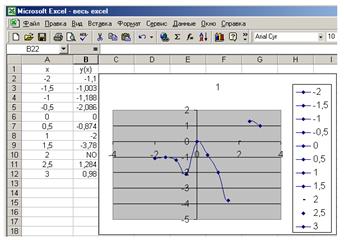
В MathCAD:
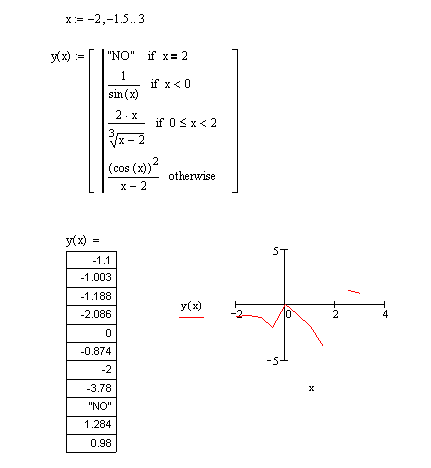
В Delphi:
var
x,Xn,Xk,h,y: Real;
begin
Xn:=strtoFloat(edit1.text);
Xk:=strtoFloat(edit2.text);
h:=strtoFloat(edit3.text);
begin
x:=Xn;
while x<=Xk+h/2 do
begin
If (x=2) then
begin
memo1.Lines.Add('No answer');
end
else
begin
if x<0 then y:=1/sin(x) else
if (x>=0) and (x<2) then y:=(2*x)/((abs(x-2)/(x-2))*(exp(1/3*(ln(abs(x-2)))))) else
if x>2 then y:=sqr(cos(x))/(x-2);
memo1.Lines.Add('y='+FormatFloat('0.000',y));
Series1.AddXY(x,y,'',clred);
end;
x:=x+h;
end;
end;
end;
end.
Вывод: т.к. ответы в Pascal, Excel, MathCAD и Delphi сошлись – решение верно.
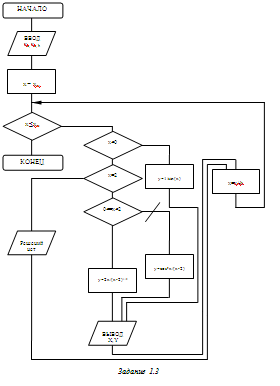
Блок-схема алгоритма решения задания: 1.2
Нахождение функции, заданной условием:
Вычислить функцию y(x) по заданному массиву x
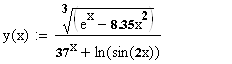

В Pascal:
program zadanie3;
uses crt;
const n=4;
var x,y:array[1..n] of real;
i:integer;
z,j,d:real;
begin
clrscr;
for i:=1 to n do
begin
write('Enter x[i]=');
readln(x[i]);
end;
for i:=1 to n do
begin
j:=exp(x[i])-8.35*x[i]*x[i];
z:=exp(1/3*ln(abs(j)))*(abs(j)/j);
d:=exp(x[i]*ln(37))+ln(abs(sin(2*x[i])))*(abs(2*x[i])/2*x[i]);
y[i]:=z/d;
writeln('x[i]=',x[i]:5:1,' y[i]=',y[i]:5:3);
end;
readkey;
end.
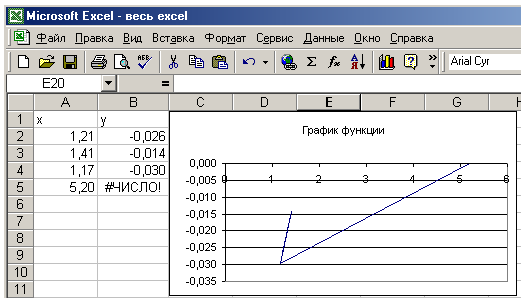
Результаты вычислений:
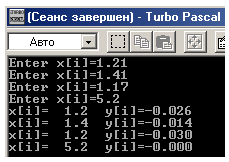
В Excel:
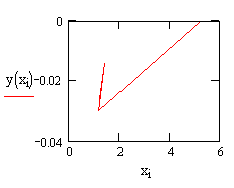
В MathCAD:

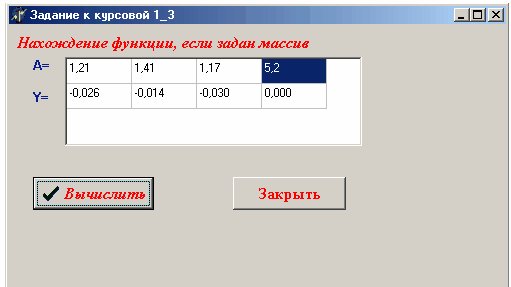
В Delphi:
var x,y:array[0..3]of real;
i:integer;
z,j,d:real;
begin
randomize;
for i:=0 to 3 do
begin
x[i]:=strtofloat(stringGrid1.cells[i,0]);
j:=exp(x[i])-8.35*x[i]*x[i];
z:=exp(1/3*ln(abs(j)))*(abs(j)/j);
d:=exp(x[i]*ln(37))+ln(abs(sin(2*x[i])))*(abs(2*x[i])/2*x[i]);
y[i]:=z/d;
stringgrid1.Cells[i,1]:=FormatFloat('0.000',y[i]);
end;
end;
procedure TForm1.BitBtn2Click(Sender: TObject);
begin
form1.close;
end;
end.
Вывод: т.к. ответы в Pascal,Excel,MathCAD и Delphi сошлись – решение верно.
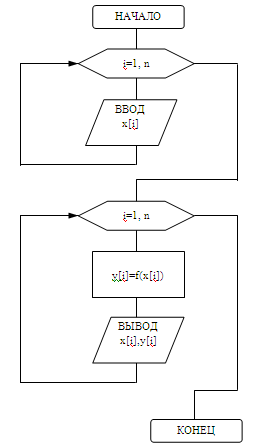
Блок-схема алгоритма решения задания №1.3
Нахождение функции заданном массиве:
Задание 1.4
Найти сумму, если задана функция y(x), задан массив а, даны Xn, n, h.
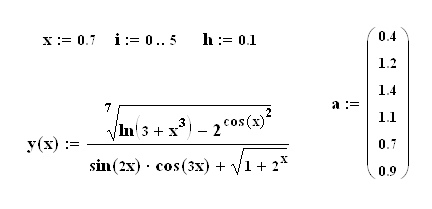
В Pascal:
Program Summa;
uses crt;
const n=6;
Var x,j,z,d,Xn,h,F,S:Real;
i:Integer;
a:array [1..n] of Real;
BEGIN
clrscr;
randomize;
Write('enter please Xn,h=');
ReadLN(Xn,h);
for i:=1 to n Do
begin
Write('enter please a[i]=');
ReadLN(a[i]);
end;
x:=Xn;
S:=0;
for i:=1 to n Do
begin
j:=(ln(abs(3+x*x*x))*(abs(3+x*x*x)/(3+x*x*x)))-(exp((cos(x)*cos(x))*ln(2)));
z:=exp(1/7*ln(abs(j)))*abs(j)/j;
d:=sin(2*x)*cos(3*x)+sqrt(1+exp((x)*ln(2)));
F:=z/d;
S:=S+F*a[i];
x:=x+h;
end;
WriteLN('S=',S:10:3);
END.
Результаты вычислений:
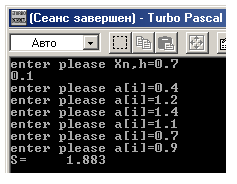
В Excel:

В MathCAD:

В Delphi:
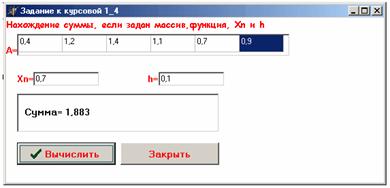
var a:array[0..5]of real;
i:integer;
x,s,Xn,z,F,j,d,h:real;
begin
Xn:=strtoFloat(edit1.text);
h:=strtoFloat(edit2.text);
x:=Xn;
s:=0;
for i:=0 to 5 do
begin
j:=(ln(abs(3+x*x*x))*(abs(3+x*x*x)/(3+x*x*x)))-(exp((cos(x)*cos(x))*ln(2))); j:=(ln(abs(3+x*x*x))*(abs(3+x*x*x)/(3+x*x*x)))-(exp((cos(x)*cos(x))*ln(2)));
z:=exp(1/7*ln(abs(j)))*abs(j)/j;
d:=sin(2*x)*cos(3*x)+sqrt(1+exp((x)*ln(2)));
F:=z/d;
a[i]:=strtofloat(stringGrid1.cells[i,0]);
s:=s+F*a[i];
x:=x+h;
end;
memo1.Lines.Add(' Ñóììà= '+FormatFloat('0.000',s));
end;
procedure TForm1.BitBtn2Click(Sender: TObject);
begin
form1.close;
end;
end.
Вывод: т.к. ответы в Pascal, Excel, MathCAD и Delphi сошлись – решение верно.
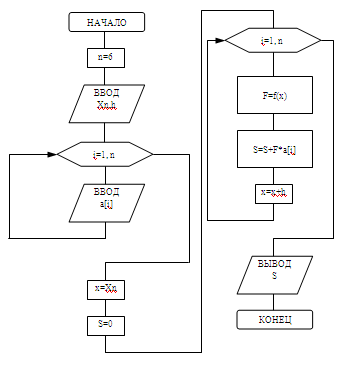
Блок-схема алгоритма решения задания №1.4
Нахождение функции, если дан x, h, n, задан массив:
Похожие работы
... при построении итерационных методов решения уравнения =0. Например взяв за корень линейного интерполяционного алгебраического многочлена, построенного по значениям и в узле или по значениям и в узлах и , приходят соответственно к методу Ньютона и метода секущих , где - разделенная разность функций для узлов и . Другой подход к построению численных методов решения уравнения ...
... вычисления значений этой функции на интервале аппроксимации. Приведение аргумента к интервалу аппроксимации является обязательным этапом как при использовании итеративных методов вычисления элементарных функций, так и при многочленной и рациональной аппроксимации. Этот прием позволяет сократить число операций необходимых для вычисления значения элементарной функции за счет уменьшения количества ...
... к гамма-функции с положительным целым параметром, гамма-функции с положительным параметром, гамма-функции для множества точек. Созданная функциональная модель реализации основных способов вычисления гамма функции и ее программная реализация могут служить органической частью решения более сложных задач. СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ и литературы 1. Бронштейн, И.Н. Справочник по ...
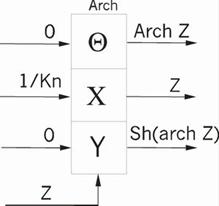
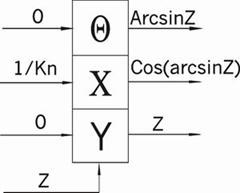
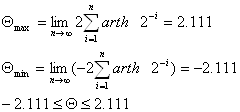
ть специализированный математический процессор для вычисления элементарных функций arcSin(Z) и arCth(Z). Эти функции можно реализовать методом Волдера «Цифра за цифрой», метод Меджита и др. Оба эти метода основаны на ряде итерационных формул, которые приведены в таблице 1.1. Основное их различие заключается в том, что в методе Меджита на первом этапе сразу рассчитываются все направляющие ...


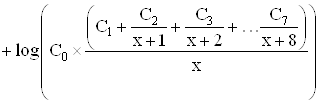
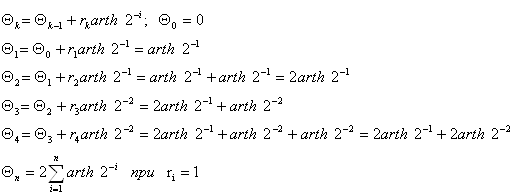
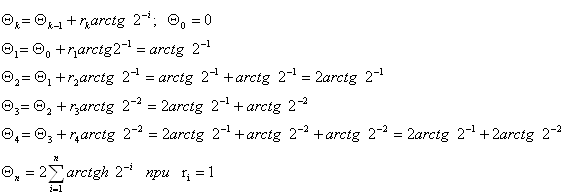
0 комментариев