Навигация
ЛИСП-реализация основных способов вычисления гамма-функции
СОДЕРЖАНИЕ
Введение
1. Постановка задачи
2. Математические и алгоритмические основы решения задачи
2.1 Понятие гамма-функции
2.2 Вычисление гамма функции
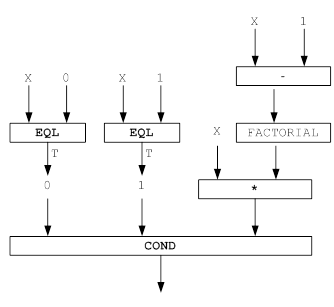
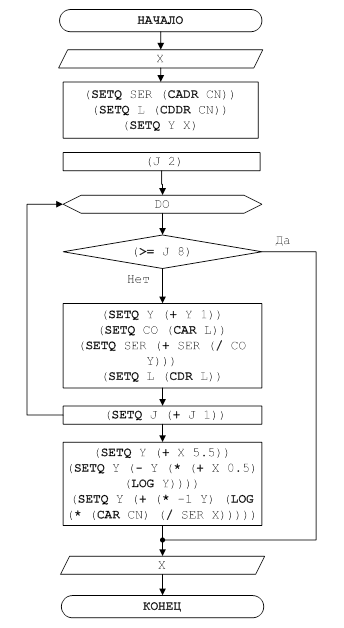
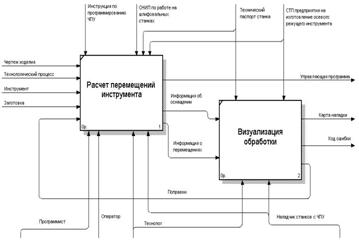
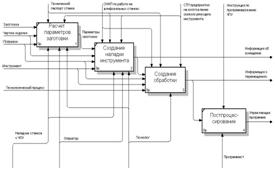
3. Функциональные модели и блок-схемы решения задачи
4. Программная реализация решения задачи
5. Пример выполнения программы
Заключение
Список использованных источников и литературы
ВВЕДЕНИЕ
Выделяют особый класс функций, представимых в виде собственного либо несобственного интеграла, который зависит не только от формальной переменной, а и от параметра.
Такие функции называются интегралами зависящими от параметра. К их числу относится гамма функции Эйлера.
Гамма функция представляется интегралом Эйлера второго рода:
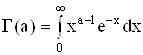 .
.
Гамма-функция расширяет понятие факториала на поле комплексных чисел. Обычно обозначается Γ(z).
Была введена Леонардом Эйлером, а своим обозначением гамма-функция обязана Лежандру.
Через гамма-функции выражается большое число определённых интегралов, бесконечных произведений и сумм рядов.
1. Постановка задачи
Требуется реализовать основные способы вычисления гамма-функции:
1. Гамма-функции для целых положительных n равна
Г (n) = (n - 1)! = 1·2... (n - 1). (1)
2. Для x>0 гамма-функция получается из ее логарифма взятием экспоненты.
![]() . (2)
. (2)
3. Гамма-функции для ряда точек:
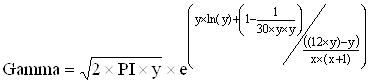 (3)
(3)
Пример 1.
Вычислить гамма-функции Г(6).
Решение:
Так как 6 – положительное целое число, воспользуемся формулой (1):
Г(6) =(6-1)! = 5! = 120
Ответ: 120.
Пример 2.
Вычислить гамма-функции Г(0,5).
Решение:
Воспользуемся формулой (2):
![]() .
.
![]() .
.
Ответ: ![]() .
.
Пример 3.
Вычислить гамма-функции Г(1,5).
Решение:
Воспользуемся формулой (3):
y = 1.5 + 2 = 3.5.
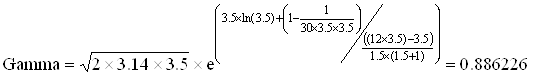 .
.
Ответ: ![]() .
.
2. Математические и алгоритмические основы решения задачи
2.1 Понятие гамма-функции
Гамма функцию определяет интеграл Эйлера второго рода
G(a) =![]() (2.1)
(2.1)
сходящийся при ![]() .
.
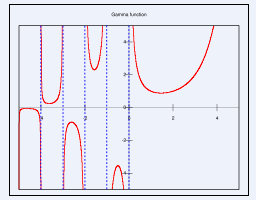
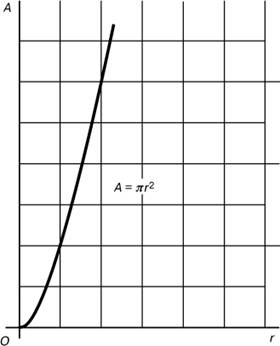
Рисунок 1. График гамма-функции действительного переменного
Положим ![]() =ty, t > 0 , имеем
=ty, t > 0 , имеем
G(a) =![]()
и после замены ![]() , через
, через ![]() и t через 1+t ,получим
и t через 1+t ,получим
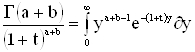
Умножая это равенство и интегрируя по t и пределах от 0 до ![]() , имеем:
, имеем:
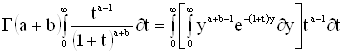
или после изменения в правой части порядка интегрирования ,получаем:
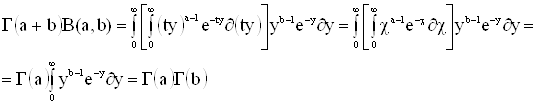
откуда
 (2.2)
(2.2)
заменяя в (2,1) ![]() , на
, на ![]() и интегрируем по частям
и интегрируем по частям
![]()
получаем рекурентною формулу
![]() (2.3)
(2.3)
так как
![]()
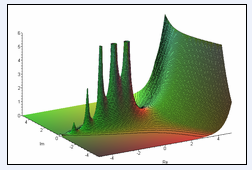
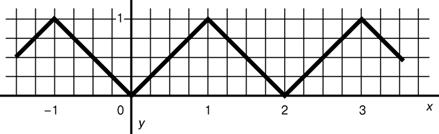
Рисунок 2. График модуля гамма-функции на комплексной плоскости
При целом ![]() имеем
имеем
![]() (2.4)
(2.4)
то есть при целых значениях аргумента гамма-функция превращается в факториал, порядок которого на единицу меньше взятого значения аргумента. При n=1 в (2.4) имеем
![]()
Похожие работы
... информационных технологий, которое заключается как в совершенствовании методов организации информационных процессов, так и их реализации с помощью конкретных инструментов – сред и языков программирования. Итогом работы можно считать созданную функциональную модель вычисления неэлементарных функций. Данная модель применима к функциям, если она не задана одной формулой посредством конечного числа ...
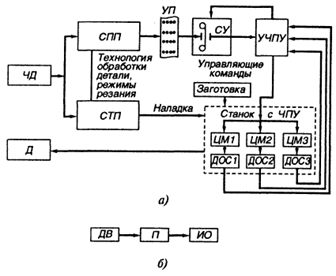
... ряде прикладных программ. Сферы применения Лиспа многообразны: наука и промышленность, образование и медицина, от декодирования генома человека до системы проектирования авиалайнеров. 3. Технологическая реализация системы подготовки обработки детали станка с ЧПУ 3.1 Описание кодов программного модуля Любой проект в Delphi состоит из нескольких частей (набора файлов, каждый из которых ...
... с приглашением по запросу (в машинной графике)required parameter обязательный параметрrequired space обязательный пробел (в системах подготовки текстов)requirements specification 1. техническое задание 2. описание требований к программному средствуrerun перезапуск, повторный запускreschedule переупорядочивать очередь (о диспетчере операционной системы)reschedule interval период переупорядочения ...
ие MSX-DOS, учитывала необходимость поддержки обширного программного обеспечения, разработанного для СР/М, и одновременно ориентировалась на новые в то время разработки, связанные с DOS. 4. Операционные системы, основанные на графическом интерфейсе Помимо широко распространенных машин, проектируемых в соответствии со сложившимися стандартами, часто создаются машины, в которых особо выделяется ...
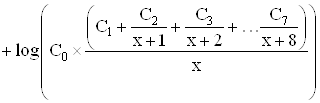

0 комментариев