Поиск минимального и максимального элемента массива и его порядкового номера (индекса)

2.9 Поиск минимального и максимального элемента массива и его порядкового номера (индекса)

Пусть требуется найти минимальный элемент (min) и его индекс (n_min) во всем массиве (in=0 и ik=n) или какой то его части (с in – го по ik – ый), в этом случаи алгоритм решения задачи можно записать так:

1.   в качестве начального значения переменной min выберем любой из рассматриваемых элементов (обычно выбирают первый). Тогда min=a_in, n_min= in;

2.  затем в цикле по параметру i начиная со следующего элемента (i=in+1, …, ik) будем сравнивать элементы массива a_i текущим минимальным min. Если окажется, что текущий (i – ый) элемент массива меньше минимального (a_i < min), то переменная min принимает значение a_i, а n_min – на i: min=a_i, n_min= i.

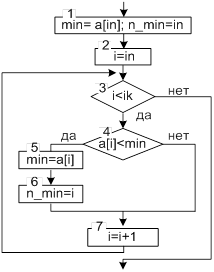
Графическая схема алгоритма и фрагмент программы поиска минимального элемента в массиве приведены на рисунке 2.16.

min=a[in]; n_min=in; for(i=in+1; i<ik; i++) if(a[i]<min) { min=a[i]; n_min=i; }

Рисунок 2.16. Графический алгоритм и фрагмент программы поиска минимального элемента в массиве

Заметим, что при наличии в массиве нескольких минимальных элементов, найден будет первый из них (самый левый минимальный элемент) при просмотре массива слева направо. Если в неравенстве a_i< min знак > поменять на знак ≥, то будет найден последний из них (самый правый минимальный элемент).

Для поиска максимального элемента max и его индекса n_max используется аналогичный алгоритм, в котором сначала надо принять max =a_in, n_ max = in, вместо неравенства a_i < min используется неравенство a_i > max. В случаи выполнения условия a_i > max записать в max =a_i и в n_ max = i.

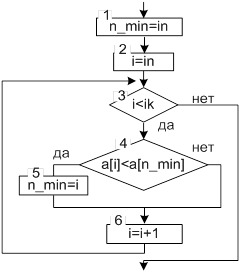
Для поиска в массиве экстремума можно не использовать вспомогательную переменную min (max). В этом случаи минимальный элемент массива определяется только по его индексу n_min (n_max) (рисунок 2.17).

/*поиск минимального элемента*/ n_min=in; for(i=in+1; i<ik; i++) if(a[i]<a[n_min]) n_min=i; /*поиск максимального элемента*/ n_max=in; for(i=in+1; i<ik; i++) if(a[i]>a[n_max]) n_max=i;

Рисунок 2.17. Графический алгоритм и фрагмент программы поиска минимального элемента в массиве по его индексу

Пример использования рассмотренных алгоритмов представлен в приложении 2.

2.10 Копирование массивов

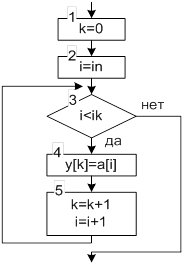
В ряде задач для организации дополнительных или промежуточных вычислений, требуется создание копии всего массива или части его элементов. Для этого можно воспользоваться алгоритмом представленным на рисунке 2.18.

k=0; for(i=in;i<ik;i++) { y[k]=a[i]; k++; }

Рисунок 2.18 Алгоритм и фрагмент программы создания копии массива

В зависимости от параметров in и ik, в массив y[ ] копируются элементы из исходного массива a[ ]. Так для копирования всех элементов массива a[ ] необходимо задать in=0, ik=n (n – количество элементов массива a[ ]). При копировании части массива, например с 3 по 9, принимаем in=2 (поскольку нумерация элементов массива в С++, начинается с нуля) и ik=9.

2.10 Формирование нового массива

В задачах формирования нового массива требуется создать массив из элементов существующего массива (массивов) удовлетворяющих заданному условию. В новый массив элементы заносятся, последовательно начиная с нулевого индекса. Максимально число элементов в формируемом массиве может достигать количества элементов в исходном массиве (массивах), минимальное значение равняется нулю. В этом случаи считается, что новый массив не сформирован.

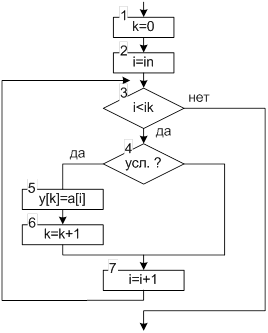
При формировании новых массивов удобно использовать динамические массивы, поскольку число его элементов заранее не известно. Алгоритм создания нового массива схож с алгоритмом копирования (рисунок 2.19).

k=0; for(i=in;i<ik;i++) { if (условие)  { y[k]=a[i]; k++; } }

Рисунок 2.19 Алгоритм и фрагмент программы формирования нового массива

Для последовательной записи элементов в новый массив используется дополнительная переменная k – счетчик элементов в новом массиве. Начальное значение этой переменной принимается равной нулю, т.е считается что в новом массиве нет элементов. При обнаружении в исходном массиве элемента удовлетворяющего заданному условию, его значение заносится в новый массив на позицию k, а после счетчик элементов увеличивается на единицу (k=k+1). Таким образом, после обработки всего исходного массива по значению счетчика k можно определить, сформирован новый массив (k>0) и сколько в нем элементов (k).

Пример 2.8

Даны два одномерных массива X и Y. Необходимо сформировать массив Z из положительных элементов массива X стоящих на четных местах и элементов массива Y больших первого элемента массива X.

массив одномерный программа алгоритм

Решение

Если число элементов массива X – n, а массива Y – m, то с учетом того, что из первого массива выбираются элементы стоящие только на четных местах, максимальное число элементов в новом массиве Z может достигать m+n/2 элементов. Поэтому для массива Z с помощью оператора динамического выделения памяти (new) выделим m+[n/2] ячейки памяти ([n/2] – целая часть от деления). Начальное значение счетчика элементов нового массива k принимается равным нулю.

При обработке массива X необходимо проверять только элементы, стоящие на четных местах, т.е. параметр цикла i изменяется от in=1 до ik=n с шагом 2. Условие отбора элементов из первого массива X[i]>0. При обработке массива Y учитываются все его элементы, т.е. параметр цикла i изменяется от in=0 до ik=m с шагом 1. Условие отбора элементов из второго массива – Y[i]> X[0].

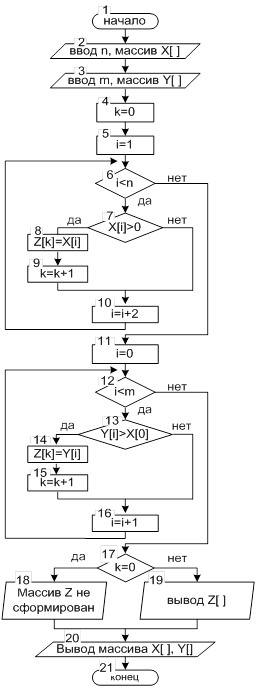
Описанный алгоритм формирования нового массива и программа представлены на рисунке 2.20.

Используемые переменные:   x[] – статический (исходный) массив; n – число элементов массива X; y[] – статический (исходный) массив; m – число элементов массива; z[] – динамический (формируемый) массив k – счетчик элементов нового массива Z; i – параметр цикла;

#include <stdio.h> main() { int k, n, m, i, x[10], y[10]; puts("Введите число элементов массива X:"); scanf("%d",&n); for(i=0;i<n;i++) { printf("x[%2d]=",i); scanf("%d",&x[i]); } puts("Введите число элементов массива Y:"); scanf("%d",&m); for(i=0;i<m;i++) { printf("y[%2d]=",i); scanf("%d",&y[i]); } int *z=new int[15]; // выделение памяти под массив Z k=0; for(i=1;i<n;i+=2) { if(x[i]>0) { z[k]=x[i]; k++; } } for(i=0;i<m;i++) { if(y[i]>x[0]) { z[k]=y[i]; k++; } } puts("Массив X:"); for(i=0;i<n;i++) printf("x[%d]=%d\n",i,x[i]); puts("Массив Y:"); for(i=0;i<m;i++) printf("y[%d]=%d\n",i,y[i]); if(k==0) puts("Массив Z не сформиро-ван."); else { puts("Массив Z:"); for(i=0;i<k;i++) printf("z[%d]=%d\n",i,z[i]); } delete[] z; // освобождение памяти }

Рисунок 2.20. Графический алгоритм и программа для примера 2.8

Литература

1.  М\ук №3089. Кравченко О.А., Мартыненко А.М. Программирование ввода–вывода данных и линейных вычислительных алгоритмов на языке С: практ. пособие к выполнению лаб. и контрол. работ по дисциплине "Вычислительная техника и программирование" для студентов техн. специальностей днев. и заоч. форм обучения Гомель: ГГТУ им. П.О. Сухого, 2005. – 33 с.

2.  М\ук №3106. Кравченко О.А., Коробейникова Е.В. Программирование разветвляющихся и циклических алгоритмов на языке С: пособие по выполнению лабораторных и контрольных работ по дисциплине"Вычислительная техника и программирование" для студентов техн. специальностей днев. и заоч. форм обучения Гомель: ГГТУ им. П.О. Сухого, 2005. – 33 с

3.  Информатика. Базовый курс : учеб. пособие / под ред. С. В. Симоновича. - 2-е изд. - Санкт-Петербург : Питер, 2007. - 639с. : ил. - (Учебник для вузов). - Библиогр.: с.631-632. - ISBN 5-94723-752-0

4.  С/С ++. Программирование на языке высокого уровня / Т. А. Павловская. - Санкт-Петербург : Питер, 2006. - 460с. : ил. - (Учебник для вузов). - Библиогр.:с.383. - ISBN 5-94723-568-4.

5.   С#. Программирование на языке высокого уровня / Т. А. Павловская. - Сант-Петербург : Питер, 2007. - 432с. : ил. - (Учебник для вузов). - Библиогр.: с.425-426. - ISBN 5-91180-174-4.

6.   Информатика : учеб. для вузов / В. А. Острейковский. - Москва : Высш. шк., 2000. - 511с. : ил. - Библиогр.: с.508. - ISBN 5-06-003533-6.

7.  Информатика: Учебник /Под ред. Проф. Н.В.Макаровой. –М.: Финансы и статистика, 1998.

8.  Касаткин А.И., Вальвачев А.Н. Профессиональное программирование на языке СИ: от Turbo C к Borland C++: Справ.пособие. – Мн.: Выш.шк., 1992. – 240 с.

9.  Топп У., Форд У. Структуры данных в С++: Пер. с англ.–М.: БИНОМ, 1994. – 816 с.

10.  Крячков А.В., Сухина И.В., Томшин В.К. Программирование на С и С++. Практикум: Учебн. Пособие для вузов. – М.: Горячая лининия – Телеком, 2000 – 344 с.

11.  Страуструп Б. Язык программирования Си++: Пер. с англ.– М.: Радио и связь, 1991. – 352 с.

Приложение Примеры решения задач по обработке одномерных массивов   Задача 1. Вычисление сумм, количеств и произведений элементов массива

Предполагается, что задан массив чисел. Программа должна:

1) вводить размерность и элементы массива;

2) вводить некоторые дополнительные числа;

3) выполнять действия в соответствии с условием задачи;

4) выводить исходные данные и результаты вычислений.

Исходные данные для отладки программы выбрать самостоятельно. Массив объявить как статический.

Задание:

В одномерном массиве A размерностью n, найти количество чисел, меньших заданного X, и произведение отрицательных чисел, стоящих на четных местах.

Решение

Таблица соответствия переменных

Переменные в задаче	Имя на языке Си	Тип	Комментарий
A[]	A[]	float	Одномерный статический массив
n	n	int	Количество элементов массива
P	P	float	Произведение отрицательных чисел
X	x	float	Заданное число
k	k	int	Количество чисел меньших X
–	k1	int	Количество отрицательных чисел
–	i	int	Номер элемента массива; параметр цикла

 

Графическая схема алгоритма

 

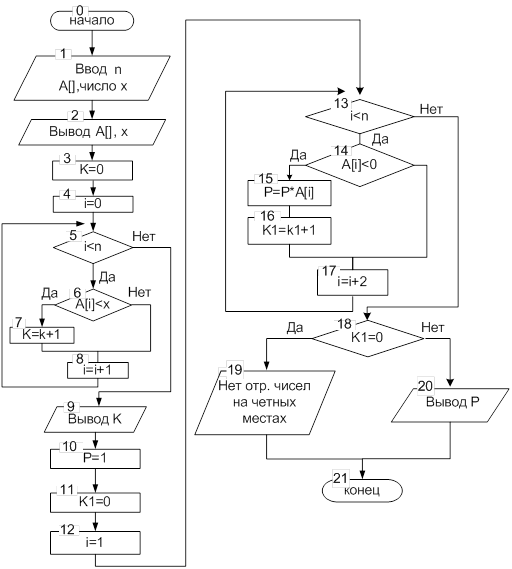
Описание алгоритма

1.  блоки 1 – 2 вводятся исходные данные;

2.  блоки 3 – 9 вычисление и вывод количества K меньших заданного X;

3.  блоки 10 – 18 вычисление количества K1 и произведения P отрицательных элементов массива стоящих на четных местах;

4.  блоки 18 – 20 проверка на наличие в массиве отрицательных чисел на четных местах и в случаи выполнения проверки вывод их произведения P.

Листинг программы

 

 #include <stdio.h>

 #include <math.h>

 main ()

 {

float P, A[10], x; //Описание переменных

int i, k1, k, n;

puts (“ Введите число x”);

scanf (“%f”, &x); // Ввод x

puts (“ Введите число элементов массива А”);

scanf (“%d”, &n);

for (i=0; i<n; i++) // Ввод массива

{

printf(“Введите число A[%d]=”, i);

scanf(“%f”, &A[i]);

}

puts(“Массив А”); // Вывод массива

for (i=0; i<n; i++)

printf(“%.2f “, A[i]);

printf(“\n”);

printf(“ x=%.3f \n”, x); // Вывод x

k=0;

for (i=0; i<n; i++)

if (A[i]<x) k=k+1; // Определение кол-ва чисел <x

printf(“ k=%d\n” ,k);

P=1;

k1=0;

for (i=1; i<n; i=i+2)

if (A[i]<0)

{  // Вычисление произведения

P=P*A[i]; // отрицательных чисел

k1=k1+1;  // стоящих на четных местах

}

if (k1==0)

printf(“В массиве на чётных местах нет отрицательных чисел \n”);

else

printf(“ P=%6.2f \n” ,P);

}

Тесты

1)   

Массив А

3.00 6.00 10.00 -7.00 -3.00 -7.00 -5.00 17.00 6.00 10.00

 x=10.000

 k=7

 P= 49.00

2)

Массив А

2.00 9.00 4.00 6.00 7.00 8.00

 x=0.000

 k=0

В массиве на чётных местах нет отрицательных чисел

Задача 2. Вычисление сумм, количеств и произведений элементов массива

Предполагается, что задан массив чисел. Программа должна:

1) вводить размерность и элементы массива;

2) вводить некоторые дополнительные числа;

3) выполнять действия в соответствии с условием задачи;

4) выводить исходные данные и результаты вычислений.

Исходные данные для отладки программы выбрать самостоятельно. Массив объявить как динамический.

Задание:

В одномерном массиве A размерностью n, найти максимальный элемент, расположенный между первым и последним нулевыми элементами массива.

Решение

Таблица соответствия переменных

Переменные в задаче	Имя на языке Си	Тип	Комментарий
max	max	int	Максимальное число
A[]	A[]	int	Одномерный динамический массив
n	n	int	Количество элементов
–	t1	int	Индекс первого нулевого элемента
–	t2	int	Индекс последнего нулевого элемента
–	i	int	Номер элемента массива; параметр цикла

 

Описание алгоритма

1.  блоки 1 – 2 ввод/вывод исходного массива A[];

2.  блоки 3 – 5 поиск первого нулевого элемента в массиве;

3.  блоки 6 – 7 проверка на наличие в массиве хотя бы одного нулевого элемента и в случаи их отсутствия вывод сообщения «В массиве нет нулей» и переход на конец алгоритма;

4.  блоки 8 – 12 поиск последнего нулевого элемента в массиве и сохранение позиции первого нуля в t1, а последнего в t2;

5.  блоки 13 – 14 проверка расположения нулевых элементов в массиве и в случаи ошибки вывод сообщения «В массиве только один ноль или они располагаются друг за другом» » и переход на конец алгоритма;

6.  блоки 15 – 21 в случаи выполнения проверки (блок 13) поиск максимального элемента между крайними нулевыми элементами и вывод полученного результата.

Графическая схема алгоритма

 

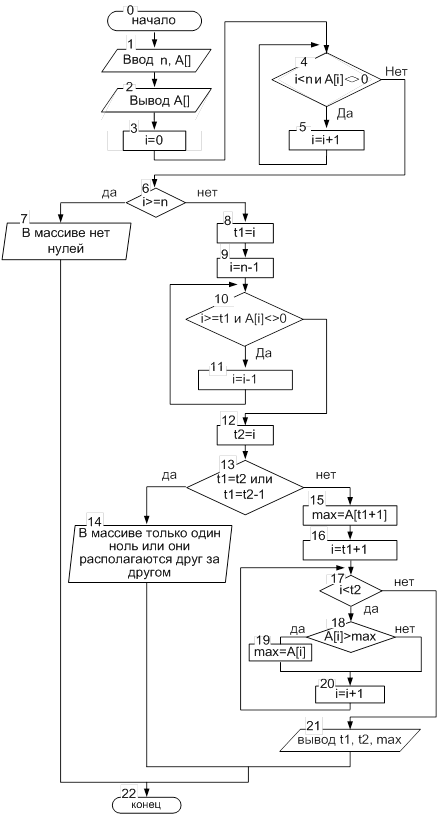
Листинг программы

 

#include <stdio.h>

main()

{

int i,t1,t2,n,max;

puts("Введите число элементов массива А");

scanf ("%d", &n);

int*A=new int[n]; //выделение памяти под массив

for(i=0;i<n;i++) //ввод массива

{

printf("a[%2d]=",i);

scanf("%d",&A[i]);

}

puts("Массив A:");

for(i=0;i<n;i++) //вывод массива

printf("a[%d]=%d\n",i,A[i]);

i=0;

while(i<n && A[i]!=0) i=i+1; //поиск позиции первого нуля

if(i>=n)

printf("В массиве нет нулей \n");

else

{

t1=i;

i=n-1;

while(i>=t1 && A[i]!=0) i=i-1; //поиск позиции последнего нуля

t2=i;

if(t1==t2 || t1==t2-1)

printf("В массиве только один ноль или они располагаются друг за другом\n");

else

{

max=A[t1+1];

for(i=t1+1;i<t2;i++)

if(A[i]>max) max=A[i]; //поиск максимального элемента

printf("t1=%d t2=%d max=%d \n",t1,t2,max);

}

}

delete[] A; // освобождение динамической памяти

 }

Тесты

 

1) Массив A: a[0]=1 a[1]=3 a[2]=0 a[3]=x6 a[4]=-3 a[5]=7 a[6]=4 a[7]=0 a[8]=1 t1=2 t2=7 max=7	2) Массив A: a[0]=0 a[1]=1 a[2]=-2 a[3]=4 a[4]=0 t1=0 t2=4 max=4	3) Массив A: a[0]=1 a[1]=2 a[2]=0 a[3]=5 a[4]=0 a[5]=3 a[6]=8 a[7]=0 a[8]=3 a[9]=1 t1=2 t2=7 max=8
4) Массив A: a[0]=1 a[1]=2 a[2]=3 a[3]=4 В массиве нет нулей	5) Массив A: a[0]=1 a[1]=0 a[2]=2 a[3]=3 a[4]=4 В массиве только один ноль или они располагаются друг за другом t1=1 t2=1 max=0	6) Массив A: a[0]=1 a[1]=2 a[2]=0 a[3]=0 a[4]=5 a[5]=2 В массиве только один ноль или они располагаются друг за другом