Движение тела, брошенного под углом к горизонту

1.1.2 Движение тела, брошенного под углом к горизонту

Точное описание характера движения тела, брошенного под углом к горизонту возможно только при рассмотрении некоторой идеальной ситуации. Будем считать, что влиянием воздуха на движение можно пренебречь.

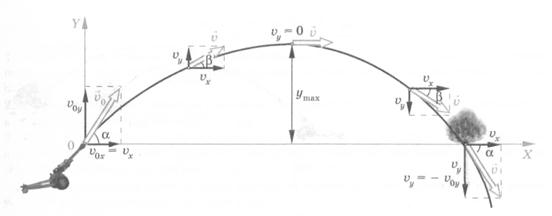
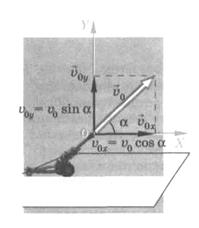
На рисунке 1.3 показана траектория движения шарика, брошенного под некоторым углом к горизонту. Траекторией движения называется кривая, отображающая положение тела в любой момент движения этого тела в выбранной системе координат. Как покажет дальнейший анализ, это знакомая из алгебры кривая, называемая параболой.

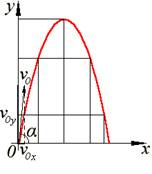
Рис. 1.3. Траектория тела, брошенного под углом а к горизонту

Если пренебречь влиянием воздуха на тело, то на тело, брошенное под углом к горизонту, как и на тело, свободно падающее, или на тело, получившую начальную скорость, направленную вертикально, действует только сила тяжести. Как бы тело не двигалось, сила тяжести может сообщить ему только ускорение g, направленное вниз. Этим и определяются и траектория движения тела, и характер его движения.

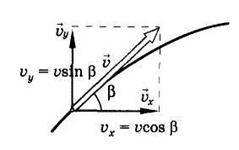
Пусть из некоторой точки O брошено тело с начальной скоростью v0, направленной под углом α к горизонту. Примем за начало отсчета координат точку, из которой брошено тело. Ось X направим горизонтально, а ось Y – вертикально вверх. Из рисунка видно, что проекции вектора v0 на оси X и Y соответственно равны v0cosα и v0sinα:

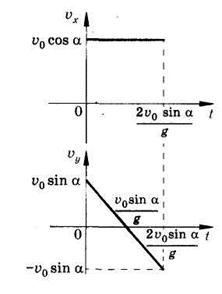
Так как на тело действует только сила тяжести, то при движении тела будет изменяться только проекция скорости v0y. Проекция же v0x изменяться не будет так же, как при прямолинейном равномерном движении:

 (1)

Координата же y изменяется так же, как при прямолинейном равномерном движении:

 (2)

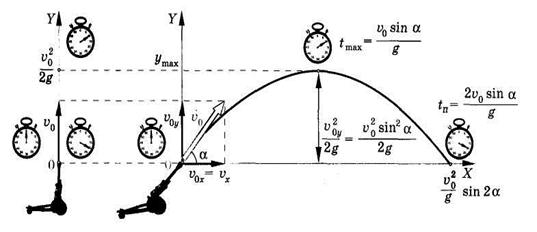
Чтобы найти траекторию движения тела, надо подставить в уравнения последовательно увеличивающиеся значения t и вычислить координаты x и y и для каждого значения t при известных значениях модуля начальной скорости v0 и угла α. По полученным данным значениям x и y нанести точки, изображающие последовательное положение тела. Соединив их плавной кривой, мы и получим траекторию движения тела. Она окажется подобной той, что изображена на рисунке 1.1. Уравнение траектории можно очень просто получить из выражений (1) и (2). Подставив выражение для времени, полученное из выражения (1) в выражение (2), легко получаем уравнение траектории движения шарика, которая оказывается параболической:

2. Рабочий проект

 

2.1 Общие сведения о работе программе (на чем написано, какие технологии использованы)

Программа написана на языке высокого уровня Visual Basic.

При разработке были использованы следующие технологии:

·  работа с массивами данных;

·  работа с таблицей DataGridView;

·  работа с библиотекой ZedGraph.dll и компонентом ZedGrarh, используемого для вывода графиков на экран;

·  работа с компонентом MenuStrip, используемого для создания меню программы.

2.2 Основные процедуры/классы системы

В программе используются следующие основные процедуры:

1.  Вычисление координат X и Y в момент времени t и заполнение списка координат list1 данными:

Dim t As New Integer

Dim Vx, Vy, x, y, g, rad, b, a1 As Double

g = 9.80665

Vx = 0, Vy = 0

x = 0, y = 0

rad = Math.PI / 180

Dim list1 As New ZedGraph.PointPairList

Dim ex As New Boolean

ex = False

t = 0

While ex = False

Vx = V * Math.Cos(a * rad)

x = Vx * t

Vy = V * Math.Sin(a * rad)

y = Vy * t - g * t * t / 2

If y < 0 Then

Dim x1, x2, y1, y2 As Double

x2 = x

y2 = y

x1 = Vx * (t - 1)

y1 = Vy * (t-1) - g * (t-1) * (t-1) / 2

a1 = (x2 - x1) / (y2 - y1)

b = y1 - a1 * x1

x = -b / a1

y = 0

ex = True

End If

list1.Add(x, y)

t = t + 1

End While

CreateGraph(zg1, list1)

zg1.Refresh()

2.  Вывод графика на экран

Private Sub CreateGraph(

ByVal zg As ZedGraph.ZedGraphControl,

ByVal list1 As ZedGraph.PointPairList)

Dim myPane As ZedGraph.GraphPane

myPane = zg1.GraphPane

myPane.Title.Text = "Движение тела, брошенного

под углом к горизонту"

myPane.XAxis.Title.Text = "X(м)"

myPane.YAxis.Title.Text = "Y(м)"

myPane.CurveList.Clear()

myPane.AddCurve("График функции", list1,

Color.DarkGray, ZedGraph.SymbolType.VDash)

myPane.Chart.Fill = New ZedGraph.Fill(

Color.WhiteSmoke, Color.Azure, 45.0F)

myPane.Fill = New ZedGraph.Fill(Color.White,

Color.FromArgb(220, 220, 255), 45.0F)

zg1.AxisChange()

End Sub

Создание новых классов для реализации в программе методов движения тела, брошенного под углом к горизонту, не потребовалось.