Поиск экстремума двумерной функции

4.  Поиск экстремума двумерной функции

Целью моделирования является, как правило, получение новых знаний об объекте моделирования. При проектировании – это определение лучшего варианта устройства, оптимальных параметров и т. д.

Любой объект исследования можно представить в виде “черного ящика” с определенным количеством входов X = (x₁, x₂, …, x_n) и выходов Y = (y₁, y₂, …, y_m). Входную переменную x_i называют фактором, а выходную переменную y_j – окликом. Зависимость Y(X) называется функцией отклика. Для получения полной информации о свойствах функции отклика в принципе необходимо проведение опытов во всех точках области определения факторов. Такой эксперимент называют экспериментом с полным перебором всех входных состояний или полным факторным анализом. Ясно, что если фактор является непрерывной переменной, то число испытаний должно быть бесконечным. Уменьшение количества испытаний при условии получения достаточно полной информации о функции отклика является целью планирования эксперимента.

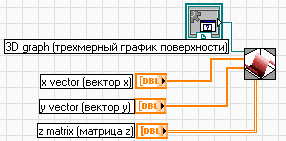
Рис. 1

В LabVIEW предусмотрена возможность визуального представления двумерной функции отклика, когда отклик и факторы заданы массивами. Для этого используется графический индикатор 3D Surface Graph (рис. 1).

На его входы “x vector” и “y vector” подаются массивы переменных х и y, а на вход “z matrix” – трехмерный массив z(x,y).

При проектировании типичной является задача оптимизации, то есть определения такой комбинации значений факторов, при которых отклик принимает экстремальное значение. Эта задача может быть решена аналитически, если установлена функциональная связь отклика с факторами, или экспериментально, когда функция отклика Y(X) неизвестна, но имеется возможность измерить значения Y при различных комбинациях уровней факторов х₁, х₂, …х_п. В последней ситуации используются поисковые методы.

5.  Поиск экстремума

В поисковых методах экстремальное значение достигается с помощью последовательных процедур:

а) определение направления движения из данной точки по результатам специально организованного эксперимента;

б) организации движения в найденном направлении и

в) многократное повторение этих процедур до достижения точки экстремума.

В LabVIEW реализованы два метода поиска экстремума: симплекс-метод наискорейшего спуска (Downhill Simplex nD) и метод сопряженных градиентов (Conjugate Gradient nD). На рис. 2 показана процедура поиска экстремума симплекс-методом. Здесь тонкими линиями изображены линии постоянного уровня отклика.

Рис 2

Рис 3

Пусть начальное значение факторов отображается точкой 1. Для организации поиска минимума двумерного отклика задаются произвольно еще две точки, так чтобы треугольник 123 был равносторонним. Для каждой точки находится значение отклика, и та точка, для которой значение отклика максимально, зеркально отображается относительно линии, соединяющей две другие точки. На рисунке – это точка 2, и она отображается в положение 4. Теперь рассматривается треугольник 134: максимальным значение отклика будет для точки 3 и она отображается в положение 5. Процедура продолжается пока не достигается точка минимума. Это будет соответствовать круговому или возвратному движению точки.

На рис. 3 показана организация градиентного поиска. Градиентом функции y(x₁, x₂) называется вектор с координатами, равными частным производным функции по соответствующим факторам. Градиент направлен в сторону максимальной крутизны поверхности отклика. Движение по направлению к минимуму производится следующим образом. Для начальной точки 1 находится градиент и в направлении обратном градиенту осуществляется перемещение на один шаг. Для новой точки опять находится градиент и производится перемещение на один шаг. И т. д., пока не будет достигнут экстремум. Признак достижения экстремума – изменение аргумента градиента на 180 градусов.

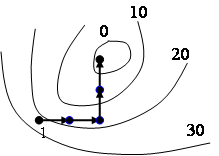
Рис. 4

Наиболее простым в реализации является метод покоординатного поиска (метод Гаусса – Зейделя). Поиск производится сначала по одной из координат до достижения местного экстремума, потом аналогично по другой координате и т.д., пока не будет достигнут экстремум функции (рис. 4). В процессе поиска постоянно сравнивается текущее значение отклика с предыдущим значением. Изменение знака этой разности говорит о достижении местного экстремума и о необходимости перехода к поиску по другой координате.

6.  Метод Гаусса-Зейделя

В лабораторной работе метод Гаусса-Зейделя используется для поиска максимума двумерной функции

z = exp{[(x – x₀)² + (y – y₀)²]/b}. (1)

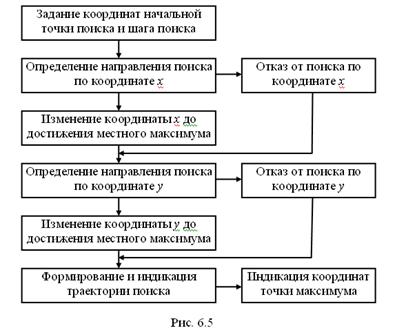
Эта функция симметрична относительно плоскостей x = x₀ и y = y₀, поэтому поиск завершается за два этапа: поиск по координате х и поиск по координате у. Структурная схема программы виртуального прибора приведена на рис. 5.

экстремум двумерная функция программный

Координаты начальной точки x_нач и y_нач и величина шага поиска Δ задаются с лицевой панели. Напомним, что шаг поиска это величина приращения координаты за одну итерацию. Шаг поиска берем одинаковым по обеим координатам: Δх = Δу = Δ.

Рассмотрим, как производится определение направления поиска. Считаем, что поиск начинается по координате х. Сначала рассчитываются значения отклика в начальной точке z = z(x_нач, y_нач) и отстоящих от нее по координате х на величину δх в сторону увеличения и уменьшения координаты: z₁ = z(x_нач + δх, y_нач) и z₂ = z(x_нач – δх, y_нач). Величина δх должна быть не больше шага поиска Δх. В зависимости от соотношения между z, z₁ и z₂ принимается решение о направлении поиска. Если z₂ < z < z₁, то координата х в процессе поиска должна увеличиваться, шаг Δх = Δ положителен. Если z₂ > z > z₁, то координата х должна уменьшаться, шаг Δх = -Δ отрицателен. Эти ситуации показаны на рис. 6 а) и в) для начальной точки, находящейся вблизи максимума.

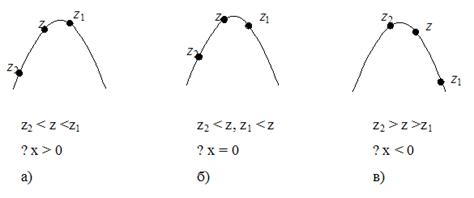
Рис. 6

Если же z > z₁ и z > z₂ (рис. 6 б), то поиск проводить не нужно, так как точки, более близкой к экстремуму, при выбранном шаге поиска нет. Анализируя записанные соотношения между z, z₁ и z₂, замечаем, что шаг Δx должен быть положительным, если z <z₁, и отрицательным, если z <z₂. В противном случае достигнут максимум и поиск не производится.

Блок-схема программы определения направления поиска приведена на рис. 7а). Текст программы записывается в структуре Formula Node (пример текста представлен на рис. 7 б).

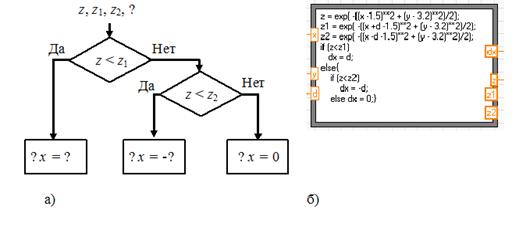
Рис. 7

После определения направления поиска производится изменение координаты х в сторону достижения максимума добавлением к х значения Δх в структуре While (рис. 8), пока вычисленное текущее значение z не станет меньше предыдущего. За максимальное значение z принимается предыдущее значение.

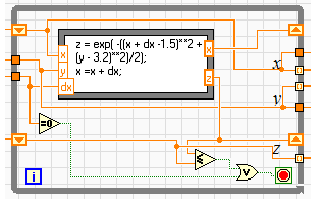
Рис. 8

Условием выхода из цикла While является равенство нулю шага поиска dx или отрицательная разность текущего и предыдущего значений z. Выводятся массивы переменных х, у и z для формирования траектории поиска и последние значения переменных х и у, которые являются начальными координатами для поиска по координате у.

Оценим ошибку определения экстремума. Ее значение можно определить, исследуя процесс поиска вблизи максимума. Рассмотрим подробнее эту ситуацию (рис. 9).Так как z(x) < z₁, то принимается решение об изменении координаты х в сторону увеличения на величину шага Δx. Тогда вычисленное значение z(х + Δх) окажется меньше предыдущего z(х) и за максимальное значение будет принято z(х).

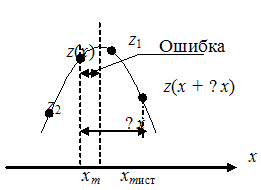
Рис. 9

Ошибка – это разность между истинной x_mист и рассчитанной x_m координатами максимума. Чему равно максимальное значение ошибки? Если уменьшать х, то z(x) будет уменьшаться, а z(х + Δх) увеличиваться. Когда они сравняются, ошибка будет равна Δх/2. При дальнейшем уменьшении х значение z(х + Δх) становится больше значения z(х) и за максимальное значение принимается z(х + Δх). Ошибка становится равной -Δх/2. Таким образом, ошибка может принимать значения от -Δх/2 до Δх/2. Если координаты начальной точки поиска равномерно распределены в области определения функции z(x, y), то и ошибка равномерно распределена в интервале (-Δх/2, Δх/2).

Видим, что на ошибку не влияет величина отклонения координаты δх, использованная при определении направлении поиска. Малое отклонение δх обеспечивает более точное измерение производной, но приводит к дополнительному шагу поиска и возвращению к исходной точке, что мы видели на примере рис. 9. Поэтому целесообразно брать δх равным максимально возможному значению, то есть шагу поиска.

Аналогично осуществляется поиск по координате у. Выходные переменные х, у и z структуры While, осуществляющей изменение координаты у, выводятся в виде массивов (как на рис 8) для формирования траектории поиска. А для индикации координат точки максимума выводятся последние значения переменных х, у и z.

Объединение массивов координат х, у и z, сформированных структурами While, производится функцией Build Array, поставленной в режим формирования одномерного массива (щелкнуть ПКМ на Build Array и в раскрывшемся меню активизировать Concatenate Inputs).

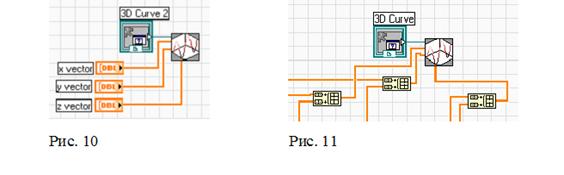
Для индикации траектории поиска используется графический индикатор 3D Curve Graph (рис. 10). Схема подсоединения к входам “x vector”, “y vector” и “z vector”, а также схема формирования массивов показана на рис. 11. На входы функций подаются одномерные массивы.

Заключение

LabVIEW обладает огромным арсеналом достоинств, таких как полноценный язык программирования, интуитивно понятный процесс графического программирования, широкие возможности сбора, обработки и анализа данных, управления приборами, генерации отчетов и обмена данных через сетевые интерфейсы.

Вместе с тем LabVIEW – очень простая и интуитивно понятная система. Неискушённый пользователь, не являясь программистом, за сравнительно короткое время (от нескольких минут до нескольких часов) способен создать сложную программу для сбора данных и управления объектами, обладающую красивым и удобным человеко-машинным интерфейсом. Например, средствами LabVIEW можно быстро превратить старый компьютер, снабжённый звуковой картой, в мощную измерительную лабораторию.

Специальный компонент LabVIEW – Application Builder, позволяет выполнять LabVIEW-программы на тех компьютерах, на которых не установлена полная среда разработки.

Список литературы

1.  Н.А. Виноградова, Я.И. Листратов, Е.В. Свиридов. «Разработка прикладного программного обеспечения в среде LabVIEW». Учебное пособие – М.: Издательство МЭИ, 2005.

2.  http://www.automationlabs.ru/

3.  http://digital.ni.com/

4.  http://www.labview.ru/

5.  http://ru.wikipedia.org/