Навигация
Слово алгоритм содержит в своем составе преобразованное географическое название Хорезм. Термин «алгоритм» обязан своим происхождением великому ученому средневекового Востока – Муххамад ибн Муса ал-Хорезми (Магомет, сын Моисея, из Хорезма). Он жил приблизительно с 783 по 850 годы, и в 1983 году отмечалось 1200-летие со дня его рождения в городе Ургенче – областном центре современной Хорезмской области Узбекистана. В латинских переводах с арабского арифметического трактата ал-Хорезми его имя транскрибировалось как algorismi. Откуда и пошло слово «алгоритм» – сначала для обозначения алгоритмов цифровых вычислений десятичной позиционной арифметики, а затем для обозначения процессов, в которых искомые величины решаемых задач находятся последовательно из исходных данных по определенным правилам и инструкциям.
Во всех сферах своей деятельности, и в особенности в сфере обработки информации, человек сталкивается с различными способами или методиками решения задач. Они определяют порядок выполнения действий для получения желаемого результата – можно трактовать это как первоначальное или интуитивное определение алгоритма. Некоторые дополнительные требования приводят к неформальному определению алгоритма.
Алгоритм – это заданное на некотором языке конечное предписание, задающее конечную последовательность выполнимых элементарных операций для решения задачи, общее для класса возможных исходных данных. Пусть D – область (множество) исходных данных задачи, а R – множество возможных результатов, тогда мы можем говорить, что алгоритм осуществляет отображение D → R. Поскольку такое отображение может быть не полным, то вводятся следующие понятия: алгоритм называется частичным алгоритмом, если мы получаем результат только для некоторых ![]() , и полным алгоритмом, если алгоритм получает правильный результат для всех
, и полным алгоритмом, если алгоритм получает правильный результат для всех ![]() .
.
Несмотря на все усилия исследователей, отсутствует одно исчерпывающе строгое определение понятия «алгоритм». Поэтому в теории алгоритмов были введены различные формальные определения алгоритма. При этом удивительным научным результатом является доказательство эквивалентности этих формальных определений в смысле их равномощности.
Варианты словесного определения алгоритма принадлежат российским ученым А.Н. Колмогорову и А.А. Маркову.
Алгоритм по Колмогорову – это всякая система вычислений, выполняемых по строго определенным правилам, которая после какого-либо числа шагов заведомо приводит к решению поставленной задачи.
Алгоритм по Маркову – это точное предписание, определяющее вычислительный процесс, идущий от варьируемых исходных данных к искомому результату.
Следует отметить, что различные определения алгоритма, в явной или неявной форме, постулируют следующий ряд требований:
− алгоритм должен содержать конечное количество элементарно выполнимых предписаний, т.е. удовлетворять требованию конечности записи;
− алгоритм должен выполнять конечное количество шагов при решении задачи, т.е. удовлетворять требованию конечности действий;
− алгоритм должен быть единым для всех допустимых исходных данных, т.е. удовлетворять требованию универсальности;
− алгоритм должен приводить к правильному по отношению к поставленной задаче решению, т.е. удовлетворять требованию правильности.
Вплоть до 30-х годов прошлого столетия понятие алгоритма оставалось интуитивно понятным и имело скорее методологическое, а не математическое значение. К началу ХХ века много ярких примеров дала алгебра и теория чисел. Среди них можно упомянуть алгоритм Евклида нахождения наибольшего общего делителя двух натуральных чисел или двух целочисленных многочленов, алгоритм Гаусса решения системы линейных уравнений над полем, алгоритм нахождения рациональных корней многочленов одного переменного с рациональными коэффициентами. К ним также можно отнести алгоритм Штурма определения числа действительных корней многочлена с действительными коэффициентами на некотором отрезке действительных чисел, алгоритм разложения многочлена одного переменного над конечным полем на неприводимые множители. Указанные алгоритмические проблемы решены путем указания конкретных разрешающих процедур. Очевидно, что для получения результатов такого типа достаточно понятия алгоритма в интуитивной интерпретации, т.е. в суждениях не алгоритмизированных, а основанных на особой проницательности, позволяющей угадывать правду. Достаточно подробно об этом пишет Р. Пенроуз в своих работах «Новый ум короля» и «Тени разума».
Однако в начале ХХ века были сформулированы алгоритмические проблемы, положительное решение которых представлялось маловероятным. Решение таких проблем потребовало привлечения новых логических средств. Ведь одно дело доказать существование разрешающего алгоритма – это можно сделать, используя интуитивное понятие алгоритма. Другое дело – доказать отсутствие алгоритма – для этого нужно знать точно, что такое алгоритм.
Начальной точкой отсчета современной теории алгоритмов можно считать работу немецкого математика Курта Гёделя (1931 год – теорема о неполноте символических логик), в которой было показано, что некоторые математические проблемы не могут быть решены алгоритмами из некоторого класса. Общность результата Гёделя связана с тем, совпадает ли использованный им класс алгоритмов с классом всех (в интуитивном смысле) алгоритмов. Эта работа дала толчок к поиску и анализу различных формализаций алгоритма.
Задача точного определения понятия алгоритма была решена в 30-х годах в работах Д. Гильберта, А. Чёрча, С. Клини, Э. Поста, А. Тьюринга в двух формах: на основе понятия рекурсивной функции и на основе описания алгоритмического процесса. Рекурсивная функция – это функция, для которой существует алгоритм вычисления ее значений по произвольному значению аргумента. Класс рекурсивных функций был определен строго как конкретный класс функций в некоторой формальной системе. Был сформулирован тезис (называемый «тезис Чёрча»), утверждающий, что данный класс функций совпадает с множеством функций, для которых имеется алгоритм вычисления значений по значению аргументов. Другой подход заключался в том, что алгоритмический процесс определяется как процесс, осуществимый на конкретно устроенной машине (называемой «машиной Тьюринга»). Был сформулирован тезис («тезис Тьюринга»), утверждающий, что любой алгоритм может быть реализован на подходящей машине Тьюринга. Оба данных подхода, а также другие подходы (А.А. Марков, Э. Пост) привели к одному и тому же классу алгоритмически вычислимых функций и подтвердили целесообразность использования тезиса Чёрча или тезиса Тьюринга для решения алгоритмических проблем.
Поскольку понятие рекурсивной функции строго математическое, то с помощью математического подхода можно доказать, что решающая некоторую задачу функция не является рекурсивной, что эквивалентно отсутствию для данной задачи разрешающего алгоритма. Аналогично, отсутствие разрешающей машины Тьюринга для некоторой задачи равносильно отсутствию для нее разрешающего алгоритма. Указанные результаты составляют основу так называемой дескриптивной теории алгоритмов, основным содержанием которой является классификация задач по признаку алгоритмической разрешимости, то есть получение высказываний типа «Задача алгоритмически разрешима» или «Задача алгоритмически неразрешима».
В данном направлении получен ряд фундаментальных результатов. Среди них – отрицательное решение в 1952 году П.С. Новиковым классической проблемы тождества для конечно определенных групп, сформулированной Деном в 1912 году. Алгоритмическая неразрешимость знаменитой десятой проблемы Гильберта, сформулированной им среди других 23 проблем в 1900 году. Задача о разрешимости диофантова уравнения. Пусть задано диофантово уравнение с произвольными неизвестными и целыми рациональными числовыми коэффициентами. Указать способ, при помощи которого возможно после конечного числа операций установить, разрешимо ли это уравнение в целых рациональных числах»), была доказана в 1970 году Ю.В. Мятиясевичем.
В технику термин «алгоритм» пришел вместе с кибернетикой. Понятие алгоритма помогло, например, точно определить, что значит эффективно задать последовательность управляющих сигналов. Применение ЭВМ послужило стимулом к развитию теории алгоритмов и изучению алгоритмических моделей, к самостоятельному изучению алгоритмов с целью их сравнения по рабочим характеристикам (числу действий, расходу памяти), а также их оптимизации. Возникло важное направление в теории алгоритмов – сложность алгоритмов и вычислений (Колмогоров). Начала складываться так называемая метрическая теория алгоритмов, основным содержанием которой является классификация задач по классам сложности. Сами алгоритмы стали объектом точного исследования, как и те объекты, для работы с которыми они предназначены. В этой области, естественно, выделяются задачи получения верхних и задачи получения нижних оценок сложности алгоритмов, и методы решения этих задач совершенно различны.
Для получения верхних оценок достаточно интуитивного понятия алгоритма. Для этого строится неформальный алгоритм решения конкретной задачи, после чего он формализуется для реализации на подходящей алгоритмической модели. Если показывается, что сложность (время или память) вычисления для этого алгоритма не превосходит значения подходящей функции при всех значениях аргумента, то эта функция объявляется верхней оценкой сложности решения рассматриваемой задачи. В области получения верхних оценок получено много ярких результатов для конкретных задач. Среди них разработаны быстрые алгоритмы умножения целых чисел, многочленов, матриц, решения линейных систем уравнений, которые требуют значительно меньше ресурсов, чем традиционные алгоритмы.
Установить нижнюю оценку – значит доказать, что никакой алгоритм вычисления не имеет сложности меньшей, чем заданная граница. Для получения результатов такого типа необходима точная фиксация рассматриваемой алгоритмической модели, и такие результаты получены только в очень жестких вычислительных моделях. В связи с этим получила развитие проблематика получения «относительных» нижних оценок, так называемая теория NP-полноты, связанная с трудной решаемостью переборных задач.
В результате продолжительных теоретических и практических изысканий были сформулированы основные требования к алгоритмам:
1. Каждый алгоритм имеет дело с данными – входными, промежуточными, выходными. Для того чтобы уточнить понятие данных, фиксируется конечный алфавит исходных символов (цифры, буквы и т.п.) и указываются правила построения алгоритмических объектов. Типичным используемым средством является индуктивное построение. Например, определение идентификатора во многих алгоритмических языках: идентификатор – это либо буква, либо идентификатор, к которому приписана справа либо буква, либо цифра. Слова конечной длины в конечных алфавитах – наиболее обычный тип алгоритмических данных, а число символов в слове – естественная мера объема данных. Другой случай алгоритмических объектов – формулы. Примером могут служить формулы алгебры предикатов и алгебры высказываний.
2. Алгоритм для размещения данных требует памяти. Память обычно считается однородной и дискретной, т.е. она состоит из одинаковых ячеек, причем каждая ячейка может содержать один символ данных, что позволяет согласовать единицы измерения объема данных и памяти.
3. Алгоритм состоит из отдельных элементарных шагов, причем множество различных шагов, из которых составлен алгоритм, конечно. Типичный пример множества элементарных шагов – система команд ЭВМ.
4. Последовательность шагов алгоритма детерминирована, то есть после каждого шага указывается, какой шаг следует выполнять дальше, либо указывается, когда следует работу алгоритма считать законченной.
5. Алгоритм должен обладать результативностью, то есть останавливаться после конечного числа шагов (зависящего от исходных данных) с выдачей результата. Данное свойство иногда называют сходимостью алгоритма.
6. Алгоритм предполагает наличие механизма реализации, который по описанию алгоритма порождает процесс вычисления на основе исходных данных. Предполагается, что описание алгоритма и механизм его реализации конечны.
Можно заметить аналогию с вычислительными машинами. Требование 1 соответствует цифровой природе ЭВМ, требование 2 – памяти ЭВМ, требование 3 – программе машины, требование 4 – её логической природе, требования 5, 6 – вычислительному устройству и его возможностям.
Имеются также некоторые черты неформального понятия алгоритма, относительно которых не достигнуто окончательного соглашения. Эти черты можно сформулировать в виде вопросов и ответов.
1. Следует ли фиксировать конечную границу для размера входных данных?
2. Следует ли фиксировать конечную границу для числа элементарных шагов?
3. Следует ли фиксировать конечную границу для размера памяти?
4. Следует ли ограничить число шагов вычисления?
На все эти вопросы далее принимается ответ «НЕТ», хотя возможны и другие варианты ответов, поскольку у физически существующих ЭВМ соответствующие размеры ограничены. Однако теория, изучающая алгоритмические вычисления, осуществимые в принципе, не должна считаться с такого рода ограничениями, поскольку они преодолимы, по крайней мере, в принципе (например, любой фиксированный размер памяти всегда можно увеличить на одну ячейку).
Таким образом, уточнение понятия алгоритма связано с уточнением алфавита данных и формы их представления, памяти и размещения в ней данных, элементарных шагов алгоритма и механизма реализации алгоритма. Однако эти понятия сами нуждаются в уточнении. Ясно, что их словесные определения потребуют введения новых понятий, для которых, в свою очередь, снова потребуются уточнения и т.д. Поэтому в теории алгоритмов принят другой подход, основанный на конкретной алгоритмической модели, в которой все сформулированные требования выполняются очевидным образом. При этом используемые алгоритмические модели универсальны, то есть моделируют любые другие разумные алгоритмические модели, что позволяет снять возможное возражение против такого подхода: не приводит ли жесткая фиксация алгоритмической модели к потере общности формализации алгоритма? Поэтому данные алгоритмические модели отождествляются с формальным понятием алгоритма.
Всякому алгоритму соответствует задача, для решения которой он был построен. Обратное утверждение в общем случае является неверным по двум причинам: во-первых, одна и та же задача может решаться различными алгоритмами; во-вторых, можно предположить (пока), что имеются задачи, для которых алгоритм вообще не может быть построен.
Как уже отмечалось, термин «алгоритм» появился в математике достаточно давно и использовался долго – под ним понималась процедура, позволявшая путем выполнения последовательности определенных элементарных шагов получать однозначный результат, не зависящий от того, кто эти шаги выполнял. Таким образом, само проведенное решение служило доказательством существования алгоритма. Однако был известен целый ряд математических задач, разрешить которые в общем виде не удавалось. Примерами могут послужить три древние геометрические задачи: о трисекции угла, о квадратуре круга и об удвоении куба – ни одна из них не имеет общего способа решения с помощью циркуля и линейки без делений.
Интерес математиков к задачам подобного рода привел к постановке вопроса: возможно ли, не решая задачи, доказать, что она алгоритмически неразрешима, т.е. что нельзя построить алгоритм, который обеспечил бы ее общее решение? Ответ на этот вопрос важен, в том числе и с практической точки зрения, например, бессмысленно пытаться решать задачу на компьютере и разрабатывать для нее программу, если доказано, что она алгоритмически неразрешима. Именно для ответа на данный вопрос и понадобилось сначала дать строгое определение алгоритма, без чего обсуждение его существования просто не имело смысла. Построение такого определения, как мы знаем, привело к появлению формальных алгоритмических систем, что дало возможность математического доказательства неразрешимости ряда проблем. Оно сводится к доказательству невозможности построения рекурсивной функции, решающей задачу, либо к невозможности построения машины Тьюринга для нее, либо несостоятельности любой другой модели. То есть задача считается алгоритмически неразрешимой, если не существует машины Тьюринга (или рекурсивной функции, или нормального алгоритма Маркова), которая ее решает.
Первые доказательства алгоритмической неразрешимости касались некоторых вопросов логики и самой теории алгоритмов. Оказалось, например, что неразрешима задача установления истинности произвольной формулы исчисления предикатов – эта теорема была доказана в 1936 г. Чёрчем.
В 1946-47 гг. А.А. Марков и Э. Пост независимо друг от друга доказали отсутствие алгоритма для распознавания эквивалентности слов в любом ассоциативном исчислении.
В теории алгоритмов к алгоритмически неразрешимой относится «проблема остановки»: можно ли по описанию алгоритма (Q) и входным данным (x) установить, завершится ли выполнение алгоритма результативной остановкой? Эта проблема имеет прозрачную программистскую интерпретацию. Часто ошибки разработки программы приводят к зацикливанию – ситуации, когда цикл не завершается и не происходит завершения работы программы и остановки. Неразрешимость проблемы остановки означает, что нельзя создать общий, пригодный для любой программы алгоритм отладки программ. Неразрешимой оказывается и проблема распознавания эквивалентности алгоритмов: нельзя построить алгоритм, который для любых двух алгоритмов выяснял бы, всегда ли они приводят к одному и тому же результату или нет.
Важность доказательства алгоритмической неразрешимости в том, что если такое доказательство получено, оно имеет смысл закона-запрета, позволяющего не тратить усилия на поиск решения, подобно тому, как законы сохранения в физике делают бессмысленными попытки построения вечного двигателя. Вместе с этим необходимо сознавать, что алгоритмическая неразрешимость какой-либо задачи в общей постановке не исключает возможности того, что разрешимы какие-то её частные случаи. Справедливо и обратное утверждение: решение частного случая задачи еще не дает повода считать возможным её решения в самом общем случае, т.е. не свидетельствует об ее общей алгоритмической разрешимости.
Роль абстрактных алгоритмических систем в том, что именно они позволяют оценить возможность нахождения общего решения некоторого класса задач. Для специалиста в области информатики важно сознавать, что наличие алгоритмически неразрешимых проблем приводит к тому, что оказывается невозможным построить универсальный алгоритм, пригодный для решения любой задачи. К подобным проблемам приводят и попытки алгоритмизировать сложную интеллектуальную деятельность человека, например, обучение других людей, сочинение стихов и пр.
2. Алгоритм как абстрактная машинаПонятие, в особенности частично рекурсивной функции, является одним из главных понятий теории алгоритмов. Значение его состоит в следующем. С одной стороны, каждая стандартно заданная частично рекурсивная функция вычислима путем некоторой процедуры механического характера, отвечающей интуитивному представлению об алгоритмах. С другой стороны, какие бы классы точно очерченных алгоритмов ни строились, во всех случаях неизменно оказывалось, что вычислимые посредством них числовые функции являлись частично рекурсивными. Поэтому общепринятой является научная гипотеза, формулируемая как тезис Чёрча: «Класс осуществляемых операций, попадающих, таким образом, под определение «алгоритма» (или «вычисления», или «выполнимой процедуры», или «рекурсивной операции»), остался бы в точности тем же самым, если мы расширим определение наших машин...».
Этот тезис дает алгоритмическое истолкование понятия частично рекурсивной функции. Его нельзя доказать, поскольку он связывает нестрогое математическое понятие интуитивно вычислимой функции со строгим математическим понятием частично рекурсивной функции. Однако исследования, проводившиеся весьма многими математиками в течение нескольких десятилетий, выявили полную целесообразность считать понятие частично рекурсивной функции научным эквивалентом интуитивного понятия вычислимой частичной функции.
Тезис Чёрча оказался достаточным, чтобы придать необходимую точность формулировкам алгоритмических проблем и в ряде случаев сделать возможным доказательство их неразрешимости. Причина заключается в том, что обычно в алгоритмических проблемах математики речь идет не об алгоритмах, а о вычислимости некоторых специальным образом построенных функций. В силу тезиса Чёрча вопрос о вычислимости функции равносилен вопросу о ее рекурсивности. Понятие рекурсивной функции строгое. Поэтому обычная математическая техника позволяет иногда непосредственно доказать, что решающая задачу функция не может быть рекурсивной. Именно этим путем самому Чёрчу удалось доказать неразрешимость основной алгоритмической проблемы логики предикатов – проблемы тождественной истинности формул исчисления первой ступени.
Точное описание класса частично рекурсивных функций вместе с тезисом Чёрча дает одно из возможных решений задачи об уточнении понятия алгоритма. Однако это решение не вполне прямое, так как понятие вычислимой функции является вторичным по отношению к понятию алгоритма. Спрашивается, нельзя ли уточнить непосредственно само понятие алгоритма и уже затем при его помощи определить точно и класс вычислимых функций? Такое направление поиска привело к построению иного, нежели рекурсивные функции, класса моделей алгоритма. Основная его идея состоит в том, что алгоритмические процессы – это процессы, которые может осуществлять определенным образом устроенная машина, моделирующая тем самым выполнение отдельных операций человеком. Функционирование такой машины и есть выполнение некоторого алгоритма.
Исходя из свойств алгоритма, можно сформулировать общие требования к таким машинам:
1. характер их функционирования должен быть дискретным, т.е. состоять из отдельных шагов (команд), каждый из которых выполняется только после завершения предыдущего;
2. действия должны быть детерминированы, т.е. шаги выполняются в строгом порядке, а их результат определяется самим шагом и результатами предыдущих шагов;
3. перед началом работы машине предоставляются исходные данные из области определения алгоритма;
4. за конечное число шагов работы машины должен быть получен результат или информация о том, что считать результатом;
5. машина должна быть универсальной, т.е. такой, чтобы с её помощью можно было бы выполнить любой алгоритм.
Чем проще структура (устройство) описанной машины и чем элементарнее ее шаги, тем больше оснований считать, что ее работа и есть выполнение алгоритма. Чтобы ответить на вопрос, какие шаги работы машины следует отнести к элементарным, вернемся к тому обстоятельству, что нас интересует преобразование информации, представленной с помощью некоторого конечного алфавита. Требование конечности алфавита является очевидным следствием того обстоятельства, что решение должно быть получено за конечное число шагов. Если информация не представлена в дискретной форме, например вещественное число, то его обработка в общем случае может содержать бесконечное число шагов, например нахождение цифр числа π или извлечение квадратного корня из числа 2. Таким образом, алгоритм оказывается конечной последовательностью действий, производимых над данными, представленными с помощью конечного алфавита. С учетом сказанного становится понятным определение алгоритма, которое дает В.М. Глушков: «Алгоритм – это любая конечная система правил преобразования информации (данных) над любым конечным алфавитом».
Пусть исходные данные из области определения алгоритма представлены посредством алфавита A и образуют при этом конечную последовательность знаков {a1…an} – такая последовательность называется словом. В результате выполнения алгоритма сформируется новое слово {b1…bm}, представленное, в общем случае, в другом алфавите B. На первый взгляд для проведения такого преобразования в качестве элементарных выделяются следующие операции (шаги):
1. замена одного знака исходного слова ai знаком bj из алфавита B;
Похожие работы
... ячейка, а имя переменной превращается в адрес ячейки. Появление этого адреса происходит в результате работы специального оператора языка (NEW), однако его значение в большинстве случаев не используется при программировании на алгоритмических языках типа Паскаль. Условимся считать, что адрес ячейки, которая будет хранить переменную А, есть А. Или, другими словами, А - это общее имя переменной и ...
... методом сведения. Идея этого метода состоит в том, что для исследуемой проблемы П доказывается, что она сводится к другой проблеме П¢, о которой известно, что она неразрешима. Взаимосвязь алгоритмических систем. В связи с существованием неразрешимых алгоритмических проблем возникает вопрос: А не может ли оказаться так, что алгоритмическая проблема, неразрешимая в одной алгоритмической ...
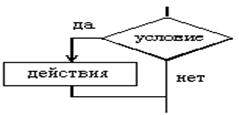
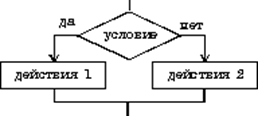
... THEN действия Полное IF Условие THEN действия 1 ELSE действия 2 Пример алгоритма ветвления на алгоритмическом языке QBasic: INPUT «1 или 2?» IF=1 OR I=2 THEN PRINT “Ок” ELSE PRINT “Вне диапазона” END IF Основные алгоритмические конструкции: Циклический алгоритм. Повторяющееся выполнение действий (групп действий),зависящее от выполнения условия, ...
... . Объясните, для чего служат разрешения и привилегии в Windows NT. Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету СИСТЕМНОЕ ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ Билет № 22 Перечислите возможности и инструменты системы программирования Microsoft Developer Studio. Укажите для чего предназначается буфер в системах ввода-вывода, ...

0 комментариев