Навигация
Является стационарным белым шумом
1. Является стационарным белым шумом.
2. Некоррелирован со входным сигналом.
3. Распределение шума равномерное в пределах ![]() .
.
Для этой статистической модели определим отношение сигнал – шум квантования:
![]() ,
( 10)
,
( 10)
где M – оператор усреднения.
Для B-разрядного квантователя можно записать соотношения:
![]() .
( 11)
.
( 11)
Тогда дисперсия шумов квантования ![]() при равномерном распределении ошибки
при равномерном распределении ошибки ![]() равна:
равна:
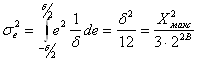 .
( 12)
.
( 12)
В случае, если ![]() , то получим выражение для отношения сигнал – шум квантования:
, то получим выражение для отношения сигнал – шум квантования:
![]() . ( 13)
. ( 13)
Обычно отношение сигнал – шум задается в дБ:
![]() .
( 14)
.
( 14)
Из выражения ( 14) следует, что добавление одного разряда кодового слова улучшает отношение сигнал – шум квантования на 6 дБ. Выражение для отношения сигнал – шум квантования получено при предположении, что диапазон квантования используется полностью, если энергия сигнала изменится, то отношение сигнал – шум квантования уменьшится. В реальных условиях дисперсия телеметрического сигнала можно меняться на 20-30дБ. По этой причине для поддержания отношения сигнал – шум квантования на заданном уровне в случае равномерного квантования необходимо увеличивать число уровней квантования, при этом увеличивается избыточность сообщения. Желательно иметь устройство квантования, при котором отношение сигнал – шум квантования не зависит от уровня сигнала. Это достигается использованием неравномерного распределения уровней квантования.
Глава 2. Неравномерное квантование мгновенных значений
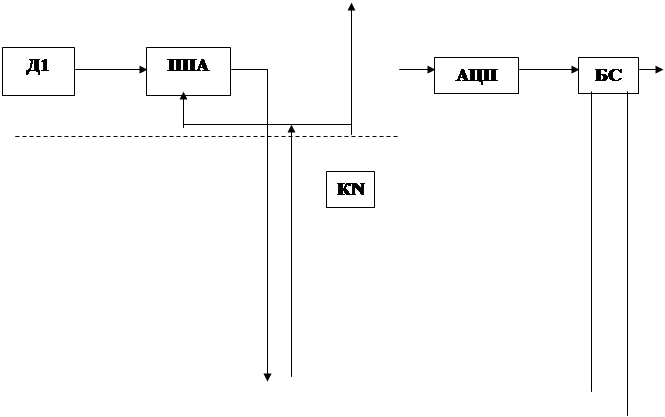
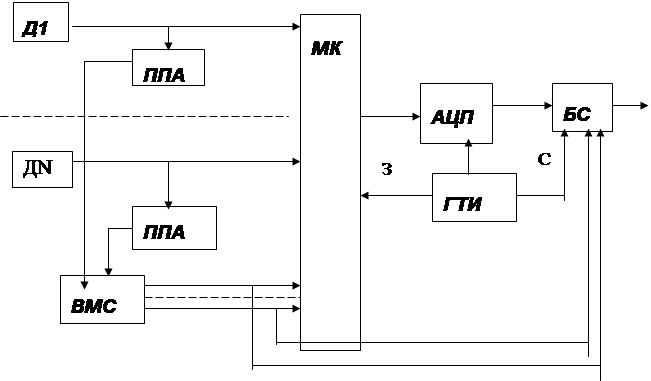
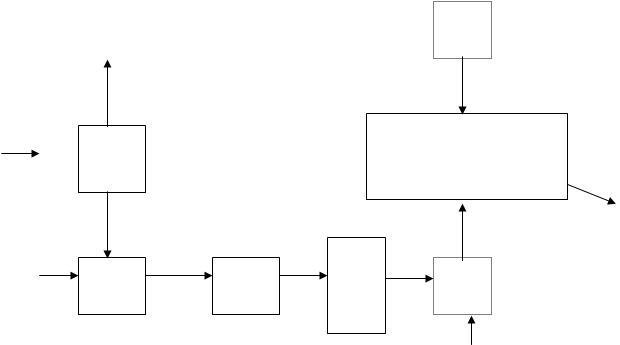
Для того чтобы относительная ошибка была постоянна при изменении дисперсии входного сигнала уровни квантования должны быть распределены по логарифмическому закону. Вместо квантования исходного сигнала можно равномерно квантовать его логарифм. В этом случае структурная схема квантователя имеет вид (рисунок 5).
Докажем, что в случае ![]() отношение сигнал – шум квантования не зависит от изменения дисперсии входного сигнала.
отношение сигнал – шум квантования не зависит от изменения дисперсии входного сигнала.
Выражение для квантованного логарифма входного сигнала имеет вид:
![]() .
( 15)
.
( 15)
Предполагается, что шумы квантования и ![]() независимы.
независимы.
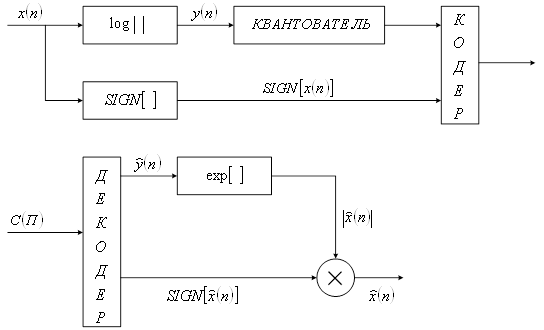
Рисунок 5
Тогда применяя обратное преобразование, получим:
![]() .
( 16)
.
( 16)
Если значение ошибки ![]() мало, то можно аппроксимировать экспоненту первыми членами ряда, т.е.:
мало, то можно аппроксимировать экспоненту первыми членами ряда, т.е.:
![]() ( 17)
( 17)
При условии, что ![]() и
и ![]() независимы
независимы ![]() и отношение сигнал – шум равно:
и отношение сигнал – шум равно:
![]() . ( 18)
. ( 18)
Следовательно, отношение сигнал - шум квантователя не зависит от мощности сигнала и зависит только от шага квантования.
Рассмотренный выше квантователь не реализуем, т.к. динамический диапазон сигнала ![]() бесконечен и требует бесконечное число уровней квантования. Для реальных случаев число уровней квантования конечно, и характеристика компрессора может быть близка к логарифмической. На практике используемые характеристики компрессора называются
бесконечен и требует бесконечное число уровней квантования. Для реальных случаев число уровней квантования конечно, и характеристика компрессора может быть близка к логарифмической. На практике используемые характеристики компрессора называются ![]() и А законами компандирования.
и А законами компандирования.
![]() - закон компандирования имеет следующий вид:
- закон компандирования имеет следующий вид:
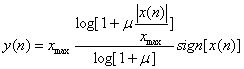 . ( 19)
. ( 19)
При малых ![]()
![]() и уровни квантования располагаются равномерно. При больших
и уровни квантования располагаются равномерно. При больших ![]() :
:
![]()
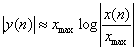 ( 20)
( 20)
и эта характеристика близка к логарифмической.
Можно показать, что чем выше значение параметра ![]() , тем ближе характеристика компандирования к логарифмической, но тем больше проигрыш в отношении сигнал/шум. Если дисперсия входного сигнала постоянна и известна, то неравномерный квантователь проигрывает равномерному. Экспериментальные исследования показали, что двенадцатиразрядное равномерное квантование имеет такое же отношение сигнал/шум, как и в случае восьмиразрядного квантования при
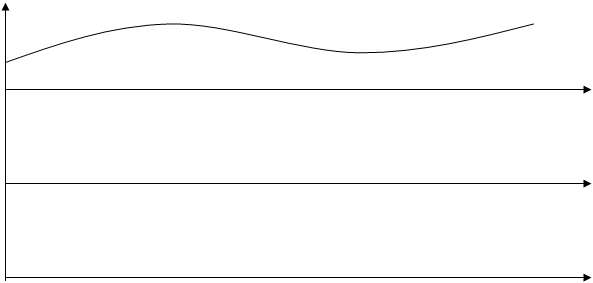
, тем ближе характеристика компандирования к логарифмической, но тем больше проигрыш в отношении сигнал/шум. Если дисперсия входного сигнала постоянна и известна, то неравномерный квантователь проигрывает равномерному. Экспериментальные исследования показали, что двенадцатиразрядное равномерное квантование имеет такое же отношение сигнал/шум, как и в случае восьмиразрядного квантования при ![]() - законе компандирования в случае речевого сигнала (рисунок 6).
- законе компандирования в случае речевого сигнала (рисунок 6).
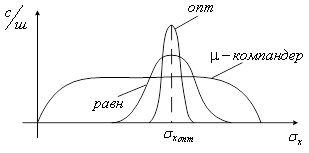
Рисунок 6
При ![]()
![]() .
.
Отношение сигнал-шум квантования для ![]() - закона компандирования равно
- закона компандирования равно
![]() ( 21)
( 21)
А - закон компандирования имеет вид:
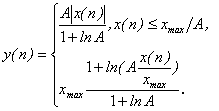 ( 22)
( 22)
Глава 3. Оптимальное квантование
Как было установлено, квантование по ![]() - закону позволяет получить постоянное отношение сигнал-шум квантователя в широком диапазоне дисперсий входного сигнала. Это достигается ценой некоторого уменьшения отношения сигнал-шум квантователя по сравнению со случаем, если диапазон квантования согласован с дисперсией входного сигнала. Когда дисперсия сигнала известна, можно так выбрать уровени и пороги квантования, чтобы минимизировать мощность шума, т.е. максимизировать отношение сигнал-шум квантователя
- закону позволяет получить постоянное отношение сигнал-шум квантователя в широком диапазоне дисперсий входного сигнала. Это достигается ценой некоторого уменьшения отношения сигнал-шум квантователя по сравнению со случаем, если диапазон квантования согласован с дисперсией входного сигнала. Когда дисперсия сигнала известна, можно так выбрать уровени и пороги квантования, чтобы минимизировать мощность шума, т.е. максимизировать отношение сигнал-шум квантователя
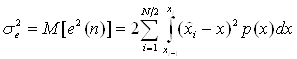 ,
( 23)
,
( 23)
![]() - ФПВ сигнала. Выражение ( 23) написано при симметричной функции плотности вероятности сигнала.
- ФПВ сигнала. Выражение ( 23) написано при симметричной функции плотности вероятности сигнала.
Требуется выбрать множество таких порогов и уровней квантования, чтобы минимизировать дисперсию входного сигнала. Для решения этой задачи продифференцируем ![]() по этим параметрам и приравняем производную к нулю
по этим параметрам и приравняем производную к нулю
 ,
,
![]() ( 24)
( 24)
![]() ( 25)
( 25)
При условии, что ![]() ,
, ![]() из выражения ( 24) и ( 25) следует, что
из выражения ( 24) и ( 25) следует, что
![]() , ( 26)
, ( 26)
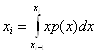 . ( 27)
. ( 27)
Т.е. оптимальные пороги равны полусумме уровней квантования, а уровни квантования есть среднее значение ФПВ сигнала на интервале ![]() .
.
Данное уравнение решается с помощью итерактивных методов для заданной ФПВ сигнала. Решение уравнения приводит к неравномерному распределению уровней квантования. Равномерное распределение уровней квантования будет только для сигналов с равномерной ФПВ. Оптимальные размеры шага квантования определены для нормального распределения, ![]() - распределения и распределения Лапласа.
- распределения и распределения Лапласа.
Оптимальный квантователь дает минимум погрешности, если известна дисперсия и форма ФПВ сигнала.
Реальные сигналы обычно нестационарны. Поэтому на практике чаще используются ![]() - квантователи, несмотря на несколько меньшее отношение сигнал-шум квантователя по сравнению с оптимальными. Обычно потери составляют 3 – 6 дБ, т.е. меньше, чем один разряд квантования при известной дисперсии входного сигнала.
- квантователи, несмотря на несколько меньшее отношение сигнал-шум квантователя по сравнению с оптимальными. Обычно потери составляют 3 – 6 дБ, т.е. меньше, чем один разряд квантования при известной дисперсии входного сигнала.
Глава 4. Адаптивное квантование
Похожие работы
... практическое применение классификации. Поэтому на практике глубина классификации обычно не превышает 10. Именно такая глубина применяется во многих классификаторах. 3. Характеристика отечественных систем классификации и кодирования товаров 3.1 Системы классификации товаров В товароведении используют следующие системы классификации товаров: - Торговая система классификации является ...
... их списывает на кодирование, что в свою очередь лишь закрепляет целевую антинаркотическую установку. Недостатки методов формирования целевой антинаркотической установки. С точки зрения современной общепсихологической теории [А.Г. Асмолов, 1979], любая попытка переформировывания личности обречена на неудачу, если она состоит в усилиях повлиять на сознание субъекта путем воздействия на сознание ...
... аппаратные затраты. 1.2 Адаптивная коммутация. Адаптивная коммутация-это способ изменения частоты опроса источников информации в соответствии со скоростью изменения входного сигнала. Основная проблема такой системы сжатия: объединение потоков отсчётов, которые идут с разной частотой, в единый поток с постоянной частотой, определяемой пропускной способностью канала. Очерёдность передачи от разных ...
... модуляцией, можно сделать вывод, что помехоустойчивость приемника, использующего в качестве информационного параметра фазу, почти приближена к вероятности ошибки приемника Котельникова. 3. Оптимальная фильтрация. Отметим, что оптимальный приемник, является корреляционным, сигнал на его выходе представляет собой функцию корреляции принимаемого и ожидаемого сигналов, благодаря чему ...

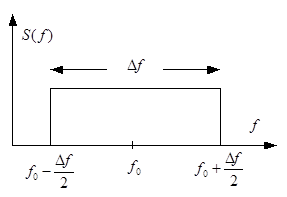



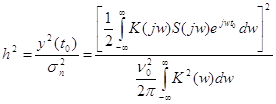
0 комментариев