Навигация
1 этап – отделение корней
|
| Создать функция пользователя |
|
| Создать ранжированную переменную x |
|
| Построить график f(x) |
Из графика видно, что приближенное значение x=1.5 (то значение x, при котором функция пересекает ось x)
2 этап – уточнение приближенного значения корня
| Специальный вычислительный блок имеет следующую структуру | |
|
| Задают начальное значение x (из графика – приближенное) |
|
| TOL – Системная переменная, которой присваивается значение требуемой точности 0.00001 |
Так как требуемая точность вычисления 0.00001, то дважды щелкнув по результату, необходимо отформатировать результат (задать нужное количество десятичных знаков).
| Given | Given (дано) – ключевое слово, открывающее блок решения |
| x3-x2 –2 = 0 | Так записывается уравнение. При записи уравнений в решающем блоке используют знак логического равенства =, которому соответствует кнопка |
|
| Вызвать функции Find, которая в качестве аргументов должна содержать искомую величины (если их несколько, то они перечисляются через запятую) |
![]()
Ответ: x=1.69562
Проверка:
Найденное значение корня подставим в заданное уравнение.
Если x найден верно, то f(x)=0 (так как мы ищем приближенное значение, то в правой части может быть не нуль, а очень малое значение < Е (требуемой точности)
Уточнение корня в программе MathCad

Задание №2
Постановка задачи:
Решить систему уравнений 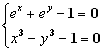 с точностью Е=0.00001
с точностью Е=0.00001
Выполнение задания №2

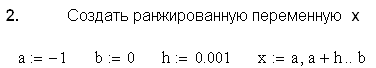
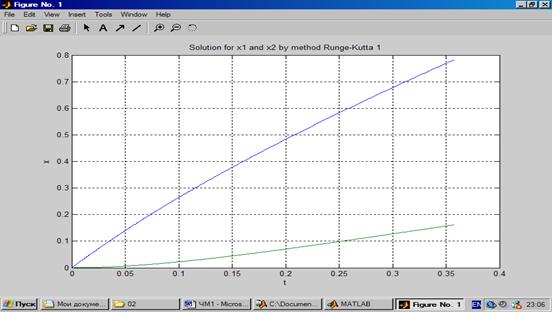
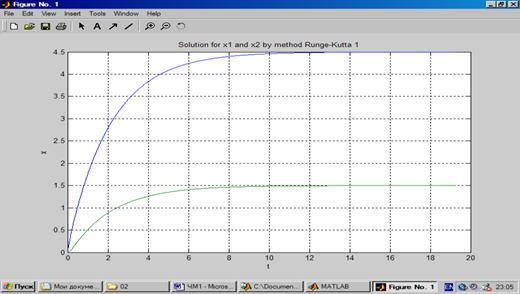
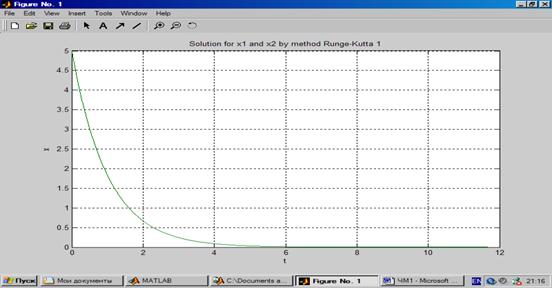
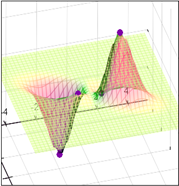
3. Построить графики функций y1 (x) и y2 (x)

4. Находим из графика точку пересечения кривых
![]()

Проверка:
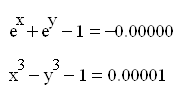
Литература
1. Симонович С. Информатика: базовый курс. – СПб.: Питер, 1999, 640 с.
2. Дьяконов В. MATHCAD 8/2000: специальный справочник – СПБ: Питер, 2001. – 592 с.
Похожие работы
... , равным максимальному шагу способа с переменным шагом, одинаково · жесткость системы затрудняет анализ результата решения ЗАКЛЮЧЕНИЕ В данной работе был исследован явный метод Эйлера для решения обычных и жестких систем ОДУ. Было проанализировано влияние величины шага интегрирования на ошибку аппроксимации, и ее влиянии на число итераций. Для этого была написана программа (Приложение 1), ...
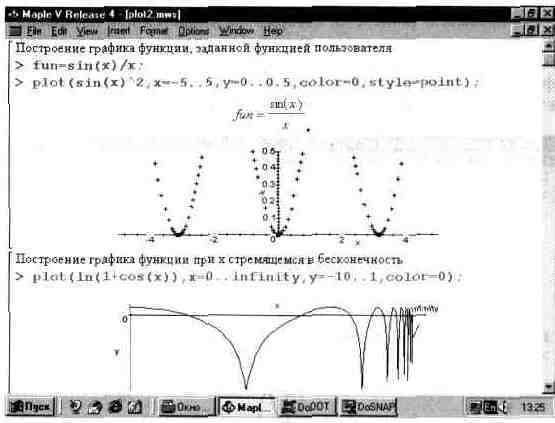
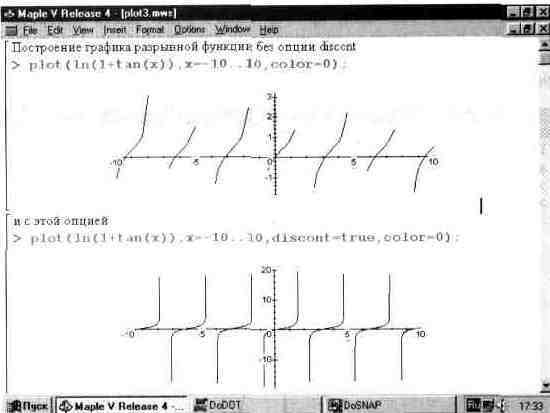
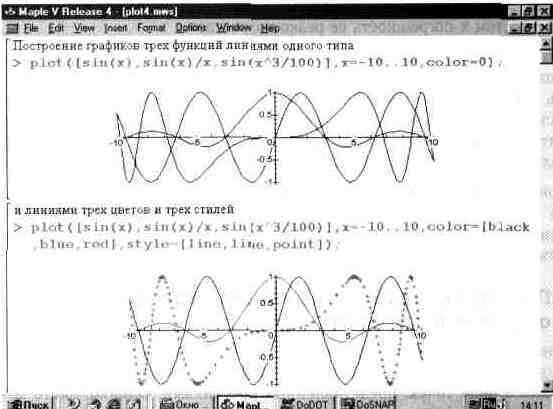
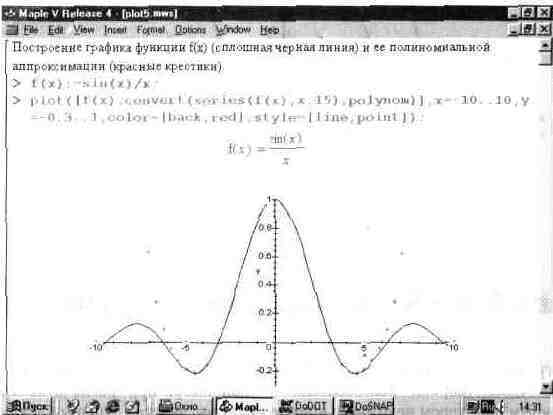
... типа MESH. 13.6. Графика пакета plots 13.6.1. Общая характеристика пакета plots Пакет plots содержит почти полсотни графических функции, существенно расширяющих возможности графики системы Maple V. В реализации R4 этот пакет содержит следующие функции: ——————————— animate Создает мультипликацию 2D графиков функций. animated Создает мультипликацию 3D графиков функции. changecoords ...
... , Флетчера-Ривса). Методы второго порядка, использующие, кроме того, и информацию о вторых производных функции f (x) (метод Ньютона и его модификации). Метод конфигураций (Хука - Дживса) Следует выделить два этапа метода конфигураций: 1) исследование с циклическим изменением переменных и 2) ускорение поиска по образцам. Исследующий поиск начинается в точке х0, называемой старым базисом. ...
... , где Fi – функция n переменных. Решением СНАУ является вектор X=(X1,…,Xn), при подстановке компонент которого в систему каждое её уравнение обращается в верное равенство. При n=3 – точка пересечения трёх поверхностей. Модифицированный метод Ньютона – один из методов, применяющихся для нахождения корня СНАУ. Модифицированный метод Ньютона предполагает наличие начального приближения X0. Суть ...



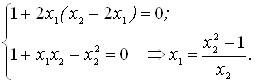

0 комментариев