Похибки суми

1. Похибки суми.

Теорема 1. Абсолютна похибка алгебраїчної суми декількох наближених чисел не перевищує суми абсолютних похибок цих чисел.

Доведення. Нехай x1, x2, …, хп – задані наближені числа. Розглянемо їх алгебраїчну суму

и = ± х1 ± х2 ± ... ± хп .

Тоді похибка цієї алгебраїчної суми Дм буде складатися з алгебраїчної суми похибок доданків, тобто

∆и = ± ∆х1 ±∆ х2 ± ... ±∆ хп .

Звідси

|∆и| ≤ |∆х1| + |∆х2| + ... +|∆хп| . (5)

Наслідок. За граничну абсолютну похибку алгебраїчної суми декількох наближених чисел можна прийняти суму граничних абсолютних похибок цих чисел, тобто

∆и = ∆х1 +∆ х2 + ... +∆ хп .

Теорема 2. Гранична відносна похибка суми декількох наближених чисел одного й того ж знака не перевищує найбільшу з граничних відносних похибок цих чисел.

Доведення. Нехай

и = + х1 + х2 + ... + хп ,

де для визначеності вважатимемо, що xi > 0 (i = 1, 2,..., п ). Позначимо

через Аi (і = 1, 2,..., п ) точні значення доданків xi , а через А – їх суму, тобто А = А1 + + А2 + ... + Ап . Тоді

δu=

Оскільки

відносний похибка наближений число

, то = Аі .

Тому

.

Нехай

max = . 1 ≤ i ≤ n

Тоді

 

тобто

 = max  1 ≤ i ≤ n

2. Похибки різниці. Розглянемо різницю двох наближених чисел х1 та х2:

и = х1-х2

Тоді, на підставі наслідку з теореми 1,

∆и = ∆х1 +∆ х2 , δu=, (6)

де А – точне значення різниці х1-х2. 3 останньої формули випливає, що для близьких чисел х1 та х2 гранична відносна похибка буде досить велика. Тому в обчислювальних алгоритмах бажано уникати віднімання близьких чисел.

Зауваження. При подальшому розгляді похибок арифметичних операцій, а також при розгляді похибок функцій (§ 6) припускатимемо, що похибки значно менші за абсолютною величиною від самих наближених величин, тож ними можна знехтувати в сумах, котрі містять одночасно наближену величину і її похибку як доданки; і завжди можна обмежитися членами, лінійними відносно похибок, нехтуючи членами більш високого порядку. Це означає, що наступні питання, пов'язані з похибками, розглядатимемо дещо грубо, проте елементарно. Адже строгий підхід під час розгляду цих питань не дає бажаних наочних результатів.

3. Похибки добутку. Нехай

Аі=хі+∆хі (і = 1,2,...,n),

де для простоти вважатимемо, що хі > 0 (і -1, 2,..., п ), А = А1 А2 … Аn , u = х1х2… хn . Тоді

А = (х1 + ∆ х1 ) (х2 + ∆ х2) ... (хп + ∆хп) =

= х1х2 … хn + х2х3 … хn ∆ х1 + х1 х3… хn ∆ х2 + ... +

+ х1х2 … хn-1 + ∆хп + ... + ∆x1∆x2…∆xn .

Враховуючи зауваження, можемо прийняти, що

А = u +x1 x2 … хп + ∆х1+ х1 х3 … хп + ∆х2 +…+ x1 x2 … хn-1 + ∆хп .

Звідси

| ∆u | = | А – u | ≤ x2x3 … xn | ∆x1| + х1 х3… xn| ∆x2| +…+ + x1 x2 … хn-1 + ∆хп . (2)

Зокрема, якщо п = 2 , то

| ∆u | ≤ x2| ∆x1| + x1| ∆x2| .

За граничну абсолютну похибку добутку можна взяти

∆u = x2x3 … xn ∆x1+ х1 х3… xn ∆x2 +…+ x1 x2 … хn-1 + ∆хп .

Розділивши нерівність (5.1) на u, одержимо

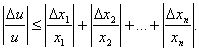
Тоді за граничну відносну похибку добутку можемо прийняти

.

4. Похибки частки. Нехай A1 = х1 + ∆ х1, A2 = х2 + ∆ х2 , де для простоти будемо вважати, що x1 > 0, x2 > 0,, .

Тоді

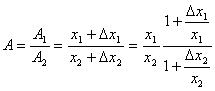 i

.

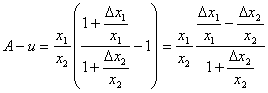Звідси

 ,

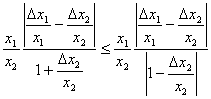aбo

.

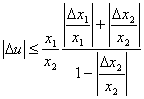Розділивши нерівність на u, одержимо

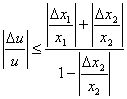
Врахувавши зауваження, замінимо  на відносну похибку 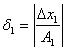 діленого,  - на відносну похибку 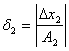 дільника,  - на відносну похибку  частки. Отримаємо

 . (8)

За граничну відносну похибку частки можна прийняти

.

5. Похибки степеня. Нехай А = (х + ∆ х)т , и = хт , де т – натуральне число, х > 0. Використовуючи похибки добутку, одержуємо

|∆u| < mxm - 1|∆x|, δ ≤ mδ1,

де δ – відносна похибка степеня; δ1 – відносна похибка аргументу х. Тому за граничні абсолютну та відносну похибки степеня можемо прийняти

∆u= mxm - 1∆x, δu= mδx . (9)

Із наведених похибок арифметичних операцій випливає, що операції додавання та віднімання (при великій різниці між числами) не погіршують точності результату порівняно з точністю алгебраїчних доданків.

Рекомендована література

1.  Цегелик Г.Г. Чисельні методи: Підручник. – Львів: Видавничий центр ЛНУ ім. І. Франка, 2004. – 408 с.

2.  Коссак О., Тумашова О., Коссак О. Методи наближених обчислень: Навч. посіб. – Львів: Бак, 2003. – 168 с.

3.  Анджейчак І.А., Федю Є.М., Анохін В.Є. і ін. Практикум з обчислювальної математики. Основні числові методи. Частина І. – Навч. посіб. Львів: Вид-во ДУ «Львівська політехніка», 2000. – 100 с.

4.  Дудикевич А.Т., Левицькa С.М., Шахно С.М. Практична реалізація методів розв’язування нелінійних рівнянь і систем: Навч.-метод. посібн. – Львів: ВЦ ЛНУ ім.. І.Франка, 2007. – 78 с.