Из названных выше трех систем автоматизации наибольшее практическое значение имеет система автоматического регулирования (САР), потому далее мы будем проводить рассуждения на основе этой системы.
Поведение автоматической системы или ее части (объекта, регулятора или отдельного звена) можно описать характеристикой – зависимостью выходного воздействия (У) от входного (Х).
Как отмечалось уже выше, различают два режима работы автоматических систем: статический, установившийся или равновесный, в котором все координаты системы постоянны, и динамический (переходный), соответствующий движению системы под влиянием управляющего воздействия или возмущения, в котором координаты системы изменяются во времени.
С точки зрения определения показателей качества регулирования, наибольший интерес представляет динамический режим. Его можно описать аналитически и графически с помощью расчетных или экспериментальных характеристик. Аналитические характеристики выражают дифференциальными уравнениями и передаточными функциями, которые определяют главные закономерности процесса движения системы, а графические – в виде графиков, где по абсциссе откладывают время, а по оси ординат – значение выходной (У) и входной (Х) величин.
Аналитическое описание динамических характеристик для простой линейной системы с одной входной и одной выходной величиной имеет вид:
![]() (4)
(4)
В уравнении m,n целые числа, коэффициенты а0-аn, b0-bn характеризуют параметры системы и являются вещественными и постоянными величинами.
Определение характеристики по данному дифференциальному уравнению высокого порядка связано с большим объемом вычислений и потому здесь используют математический аппарат для упрощения данного уравнения. Для этого в представленном уравнении переменные заменяют их изображением по Лапласу, что позволяет заменить функцию вещественного переменного х(t) (оригинал) функцией комплексного переменного (изображение), а символ d/dt заменить на сомножитель р, т.е. d/dt=p, где р - комплексная переменная. Применив преобразование Лапласа к дифференциальному уравнению системы, получим алгебраическое уравнение в операторной форме:
![]()
![]() (5)
(5)
С уравнением в операторной форме можно обращаться как с обычным алгебраическим уравнением. В частности из него можно определить передаточную функцию системы.
Передаточная функция W(p) это отношение комплексного выражения выходной величины к комплексному выражению входной величины:
W(p)=y(р)/x(р) (6)
Аналитическое описание динамической характеристики позволяет исследовать устойчивость регулирования, форму переходного процесса и показатели качества регулирования.
Однако на практике часто используют экспериментальные динамические характеристики, которые можно определить, не располагая математическим описанием, с помощью активного эксперимента. Экспериментальные динамические характеристики показывают, как реагирует система или отдельное ее звено на типовые возмущения – ступенчатое или гармоническое. Их получают путем скачкообразного или периодического изменения входной величины х(t) либо возмущения (fn) и определения изменения выходной величины у(t) в функции времени.
Такой метод менее трудоемок, чем составление аналитических уравнений, дает более наглядное представление о закономерности движения системы и возможность определения показателей качества регулирования по динамической кривой. Кроме того, знание зависимости между выходной и входной величинами позволяет определить закон управления и проводить настройку регулятора на оптимальный динамический режим.
Ступенчатое однократное изменение входного сигнала f(t)=Хвх дает временную характеристику, называемую переходной (рисунок 9 ). При этом х(t)=0 для t<t1, х(t)=const для t>t1.
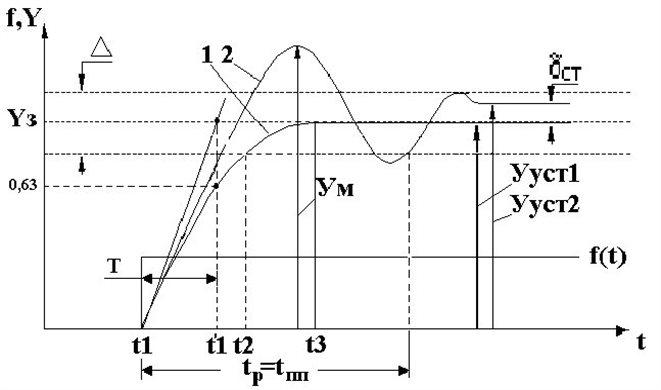
Рисунок 9 – Переходная характеристика
Единичное, ступенчатое воздействие является весьма распространенным на практике. Это включение различных аппаратов в работу соединением цепи питания, мгновенный сброс или приложение нагрузки на двигатель муфтой сцепления и т.д. По виду у(t) можно определить динамические свойства системы в ее свободном движении. Так на рисунке 9 (кривая 1) видно, что система плавно переходит из одного состояния (до момента t1) в другое состояние (после t3) и монотонно приближается к новому состоянию, не переходя его. Система не совершает колебаний относительно нового состояния, что свидетельствует об ее устойчивости в стремлении к новому состоянию. Из характеристик так же видно, что система обладает инерционностью, так как её переход в момент t1 не мгновенный. Этот переход растянут во времени до момента t3, что дает запаздывание в процессе регулирования системы и сдвигу по фазе между изменением регулирующего воздействия и изменением регулируемой величины.
На том же рисунке 9 кривая 2 показывает, что система переходит из одного состояния в другое, совершая колебания около нового установившегося значения (Ууст). Эти колебания затухающие, следовательно система приближается к новому состоянию и потому она устойчива. На кривой 2 так же наблюдается инерционность системы, перерегулирование (Ум) и остаточная статическая ошибка (dст).
Периодическое изменение входного сигнала Хвх обычно задают синусоидальным и в линейной САР получают на выходе реакцию системы в условно установившемся режиме. Эта реакция (выходное воздействие Увых) в линейной САР будет также изменятся по синусоидальному закону, так как она будет создана входным сигналом, и отличается по амплитуде за счет коэффициента передачи системы и по фазе за счет инерции системы.
Амплитуду входного сигнала задают постоянной, но изменяют его частоту. В результате проверяется способность САР к обеспечению качества регулирования в динамическом режиме разной напряженности.
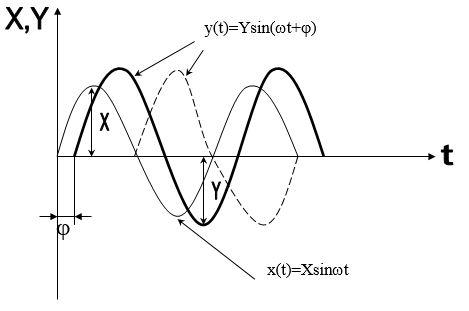
Рисунок 10 – Передача гармонического сигнала через линейную систему
Входной гармонический сигнал х=ХSinwt (рисунок 10) в установившемся режиме, т.е. после завершения переходного процесса, создает на выходе системы вынужденные гармонические колебания у=УSin(wt+j). Выходной сигнал отстает от входного сигнала на интервал за счет инерционности системы. По времени этот интервал постоянный для конкретной системы, но за счет изменения частоты входного сигнала длительность периода колебания изменяется и упомянутый интервал будет занимать разный угол внутри этого периода. Чем выше частота входного сигнала, тем больше угол j и при j=180° выходной сигнал станет полностью противофазным входному сигналу. На рисунке 10 сдвиг j = 180° показан пунктирной кривой. В системе автоматического регулирования такая ситуация вызывает неустойчивость регулирования, потому что регулятор вместо противодействия отклонению параметра объекта начнет содействовать отклонению при j = 180°. В этой связи анализ поведения САР на различных частотах необходим.
Если при постоянной амплитуде и фазе входного колебания изменять его
частоту и измерять амплитуду и фазу выходного сигнала в установившемся режиме, то можно определить следующие частотные характеристики.
Амплитудная частотная характеристика (АЧХ) А (w) = У(w)/Х(w). Это зависимость от частоты отношения амплитуд выходного сигнала ко входному сигналу.
Фазовая частотная характеристика (ФЧХ) j(w). Это сдвиг по фазе выходного сигнала относительно входного сигнала в зависимости от частоты.
Амплитудно-фазовая частотная характеристика (АФЧХ)
W(jw)= У/Х показывает зависимость отношения комплексного значения выходного сигнала к комплексному значению входного сигнала от частоты входного сигнала. Другими словами АФЧХ это комплексный передаточный коэффициент САР.
Из трех названных частотных характеристик наибольшее практическое значение имеет АФЧХ, которую можно построить в прямоугольных либо полярных координатах. В первом случае, по оси абсцисс откладывается вещественная часть, а по оси ординат - мнимая часть АФЧХ. Во втором случае выходной сигнал изображают радиус-вектором для каждой частоты входного сигнала. Длина радиус-вектора равна амплитуде выходного сигнала А(w), а угол между этим вектором и положительной полуосью абсцисс равен сдвигу по фазе выходного воздействия относительно входного, которое всегда находится на положительной полуоси абсцисс и не показывается. В результате изображением АФЧХ служит так называемый годограф вектора, т.е. геометрическое место точек, которое очерчивает конец вектора выходного воздействия вращаясь вокруг начала координат (рисунок 11) за счет изменения сдвига по фазе в диапазоне частот 0¸¥. Один из моментов такого вращения, для частоты w1, показан фазовым сдвигом j(w)=50о и А(w)= 2/3Кр. Указанная амплитуда определяется путем поворота вектора А(w) против часовой стрелки и наложением на положительную полуось абсцисс.
Годограф АФЧХ наглядно показывает поведение системы в различных условиях, в том числе и в условиях неустойчивости. Так на рисунке 11 видно, что фаза выходного сигнала не более 140°. Это означает, что система не достигает критической фазы 180° и работает в устойчивом режиме при любой частоте воздействий на систему.
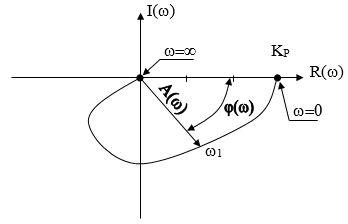
Рисунок 11 – АФЧХ
Все приведенные характеристики представляют собой различные формы описания одних и тех же свойств элементов или систем. Имея одну характеристику, можно получить любую другую. По этим характеристикам определяют показатели качества регулирования.
Рассмотрим общепринятые количественные оценки качества.
Статическая точность САР определяет остаточное отклонение параметра регулирования после окончания процесса регулирования. Эта точность определяется статической ошибкой регулирования (dст). По переходной характеристике (кривая 2, рисунок 9) статическая ошибка определяется по зависимости dст=[(Ууст-Уз)/Уз]·100% . Системы автоматического регулирования, в которых статическая ошибка равна нулю, называются астатическими. Системы, имеющие статическую ошибку, называются статическими.
Динамическая точность САР определяется максимальным динамическим отклонением (Ум, рисунок 9) в ходе процесса регулирования (tp=tпп). Это отклонение называют динамической ошибкой регулирования. Системы, работающие в длительном колебательном режиме, имеют постоянную динамическую ошибку, снижающую точность регулирования.
Перерегулирование характеризует склонность системы регулирования к колебательному режиму. С физической точки зрения перерегулирование это переход состояния САР и, прежде всего её параметра регулирования, через заданное значение в процессе регулирования с образованием нового отклонения противоположного знака. Оно имеет место в системах с переходным процессом вида кривой 2 на рисунке 9 и определяется по зависимости s=[(Ум-Ууст)/Ууст]·100 %. Перерегулирование Ум на рисунке 9 возникло вследствие перехода величины У через заданное значение Уз. Считается нормальным, если перерегулирование не превышает (10¸30)% . Но иногда перерегулирование совсем недопустимо. Например, при автоматическом управлении углом наклона отвала грейдера, в процессе планирования дорожного полотна, перерегулирование создаст волнообразную поверхность дорожного полотна, что естественно недопустимо. В этом примере так же недопустим переходный процесс по кривой 2, рисунок 9.
Время регулирования характеризует быстродействие САР. Оно определяется интервалом tp=tпп на рисунке 9, т.е. продолжительностью переходного процесса от момента поступления возмущения f(t) до момента, когда отклонение (У) по отношению к новому установившемуся (Ууст) значению не превышает допустимую зону разброса (D). Другими словами время регулирования (tp) это время приближения параметра регулирования к заданному значению с заданной точностью (например D=5% ). На практике зона разброса обычно составляет (3¸5) % и симметрична относительно установившегося значения. Для кривой 1 на рисунке 9 время регулирования определяется интервалом t1 ¸t2 .
В связи с тем, что результат определения времени регулирования зависит от принятой зоны разброса, результаты определения этого времени у разных авторов окажутся разными, потому быстродействие САР оценивают константой под названием – постоянная времени. Постоянная времени – это длительность интервала времени за который переходный процесс завершается на 63%.
Колебательность процесса регулирования определяется числом колебаний за время регулирования. Она характеризует степень устойчивости процесса регулирования. Чем больше колебательность, тем ниже степень устойчивости процесса регулирования. Уменьшение колебательности ускоряет стабилизацию процесса регулирования на заданном значении.
Устойчивость регулирования САР это способность САР возвращаться к равновесному (статическому) состоянию после принудительного ее вывода из этого состояния каким-либо воздействием. Устойчивость – это важнейшее условие работоспособности САР. Если устойчивость не выполняется, то теряется смысл определения остальных оценок качества регулирования. Устойчивость определяется по характеру изменения динамических характеристик. А запас устойчивости количественно определяется по АФЧХ.
Похожие материалы
... /U = 24.5/24 = 1.02 А - загальний споживаний струм. Отже для живлення четвертого контролера потрібно: (1020+280)/З00 = 3.8/2 = 1.9 = 2 блока БП-21 Для функціонування системи автоматизації необхідне її електричне живлення. Проектування систем електроживлення ведуть на основі завдання на основі проектування функціональної схеми автоматизації (аркуш 1), принципових електричних схем управління, ...
... информацию за предыдущие периоды, иначе отчет нарастающим итогом за год придется тоже делать на бумаге. Вот в чем состоит болезненность срыва сроков автоматизации. Расценки и порядок определения стоимости услуг по автоматизации бухгалтерского и управленческого учета. Порядок определения стоимости услуг по автоматизации строится на двух принципах: 1. Объем работ по автоматизации того или иного ...
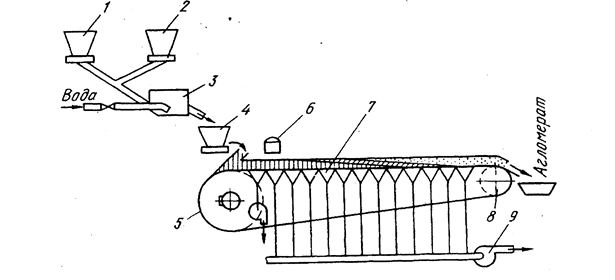
... -блочную структуру управления, а также степень оснащения объекта управления устройствами контроля и управления. На функциональной схеме в дипломном проекте изображена система автоматизации процесса спекания агломерата на агломерационной фабрике ОАО «ММК им. Ильича» (лист 3). В соответствии с поставленными задачами разработаны контуры: - автоматического контроля температуры в зажигательном ...
... ” и пользоваться мощной консультативной поддержкой фирмы изготовителя или торговой аудиторской компании у которой приобреталась программа. 3.6.3. СуперМенеджер Многовалютная система, предназначенная для автоматизации бухгалтерского учета на предприятиях сложной структуры различных форм собственности. Работа в различных компьютерных сетях и на компьютерах IBM и Macintosh. Система ...


0 комментариев