 МИНОБРНАУКИ РОССИИ
МИНОБРНАУКИ РОССИИ
федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Балтийский государственный технический университет «ВОЕНМЕХ» им. Д.Ф. Устинова»
(БГТУ «ВОЕНМЕХ» им. Д.Ф. Устинова»)
Факультет - Е «Оружие и системы вооружения»
Кафедра - Е3 «Средства поражения и боеприпасы»
Дисциплина - «Теоретическая механика»
КУРСОВАЯ РАБОТА
«Исследование динамики систем с трением»
Выполнил студент
группы Е-331
Номер группы
Калякин А. В.
Фамилия И.О.
Проверил
Фамилия И.О.
САНКТ-ПЕТЕРБУРГ 2015г.
Оглавление
Постановка задачи стр.3
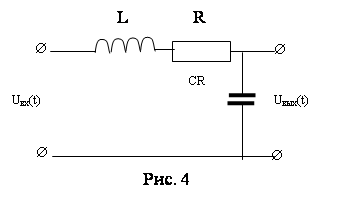
Схема системы с трением стр.4
Нахождение зависимости скорости центра масс катка от угла поворота стр.5
Нахождение скорости центра масс катка в зависимости от времени стр.9
Нахождение зависимости углового ускорения барабана от времени стр.10
Нахождение натяжения свободных участков троса в зависимости от времени стр.11
Проверка системы на наличие проскальзывания при движении стр.13
Модель движения системы с проскальзыванием стр.11
Постановка задачи
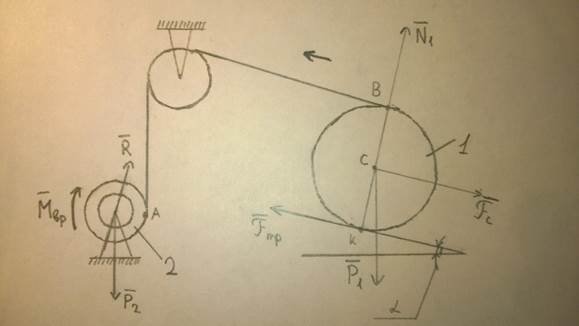
К барабану 2 приложен постоянный вращающий момент Мвр=М0. На барабане закреплен невесомый нерастяжимый трос, который перекинут через неподвижный блок и охватывает каток 1, перекатывающийся по неподвижной наклонной плоскости, образующей угол α с горизонтом. Каток 1 – однородный цилиндр веса Р1 и радиуса r1. Барабан 2 имеет вес Р2 и радиус r2, масса его равномерно распределена по ободу. К центру масс катка приложена силы сопротивления, выражающаяся зависимостью F=P1*f*cosα*vc2, где f – постоянный коэффициент, vc– скорость центра масс катка. Трением качения, трением в оси барабана и блока, массой блока пренебречь. В начальный момент времени система находилась в покое.
| r1 м | r2 м | P1 Н | P2 Н | Мвр=M0 Нм | α град. | Дополнительные сведения |
| 0,30 | 0,15 | 350 | 20 | 70 | 15 | f=0.05 м-2с2 |
1. Определить в отсутствие проскальзывания катка по наклонной плоскости:
а) зависимость угловой скорости катка от его угла поворота;
б) скорость центра масс катка в зависимости от времени;
в) зависимость углового ускорения барабана от времени;
г) натяжение свободных участков троса в зависимости от времени;
2. Найти условие качения катка по наклонной плоскости без проскальзывания.
3. Промоделировать движение системы в случае нарушения условия качения без проскальзывания, приняв зависимость коэффициента трения скольжения от скорости точки проскальзывания ![]() К в виде
К в виде
![]()
Параметры a, b, c, d выбрать самостоятельно. Результаты проиллюстрировать.
Решение
1.Определить в отсутствие проскальзывания катка по наклонной плоскости
а) зависимость угловой скорости катка от его угла поворота
Кинетическая энергия системы:
Т=Т1+Т2;
Кинетическая энергия (1) при плоскопараллельном движении:
![]() ;
;
Осевой момент инерции:
![]()
![]()
Так как (1) – сплошной однородный диск.
Выразим vc через ![]() ;
;
![]() К – мгновенный центр скоростей (1):
К – мгновенный центр скоростей (1):
![]() ;
;
Подставим в формулу кинетической энергии диска (1):
![]() ;
;
Кинетическая энергия (2) при вращательном движении:
![]()
Осевой момент инерции:
![]()
![]()
Так как масса равномерно распределена по ободу.
Выразим ![]() через
через ![]() :
:
![]()
![]()
Так как трос нерастяжим.
![]()
![]()
![]()
![]()
![]()
Обозначим:
![]()
![]()
![]()
Силы, приложенные к механической системе:
Мвр – вращательный момент совершает положительную работу на перемещении ![]() ;
;
Вес Р2, а так же реакция в оси подшипника – работу не совершают не совершают так как приложены к неподвижной точке;
Вес Р1 совершает отрицательную работу на перемещении dxc, так как точка его приложения C поднимается;
Реакция наклонной плоскости N1 работу не совершает так как перпендикулярна перемещению;
Сила сопротивления Fc совершает отрицательную работу на перемещении dxc, так как препятствует перемещению;
Сила трения Fтр в отсутствие проскальзывания работу не совершает, так как приложена к неподвижной точке.
Элементарная работа внешних сил:
![]()
Выразим ![]() ,
, ![]() через
через ![]() , используя кинематические выражения полученные выше.
, используя кинематические выражения полученные выше.
![]()
![]()
Подставим в уравнение элементарной работы:
![]()
Обозначим:
![]()
![]()
![]()
![]()
Тогда:
![]()
Теорема об изменении кинетической энергии:
![]()
![]()
![]()
![]()
![]()
![]()
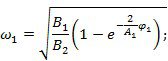
б) скорость центра масс катка в зависимости от времени
Разделим (*) на dt:
![]()
![]()
![]()
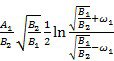 ( при |
( при |![]() |<
|<![]() ) = t
) = t
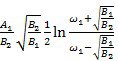 (при |
(при |![]() |>
|>![]() ) = t;
) = t;
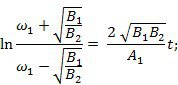
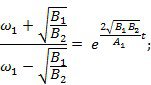
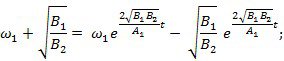
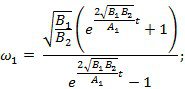
vc = 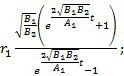
в) зависимость углового ускорения барабана от времени
Из (**):
![]() ;
;
![]()
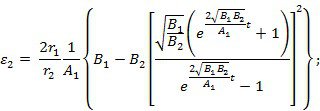
г) натяжение свободных участков троса в зависимости от времени
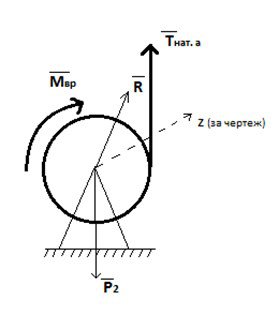 |
Уравнение кинетического момента в проекции на ![]()
![]()
![]()
![]()
![]()
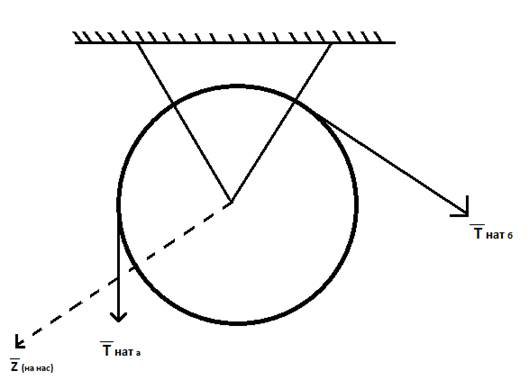
Уравнение кинетического момента в проекции на ось ![]() :
:
![]() ;
;
![]()
![]()
![]()
![]()
2) Найти условие качения катка по наклонной плоскости без проскальзывания 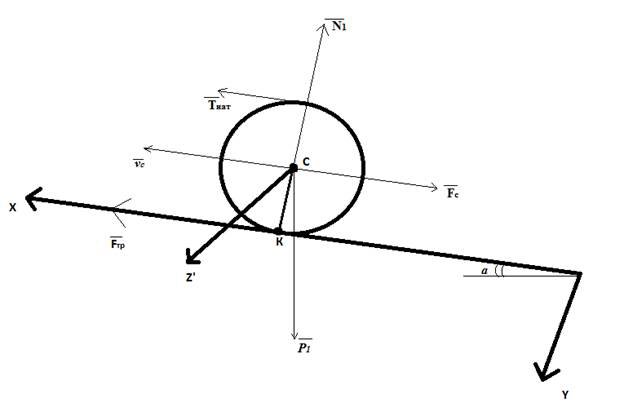
Уравнение плоскопараллельного движения (1):
1) ![]()
2) ![]()
N1=P1![]() ;
;
3) ![]() ;
;
Условия качения без проскальзования:
Б) Кинематическое:
|![]() |=
|=![]() |
|![]() |;
|;
![]()
Продифференцируем по t:
![]()
3’) ![]()
![]()
![]() ;
; ![]()
Б)Статическое:
![]()
Где ![]() – максимальное значение коэффициента трения покоя при скорости точки касания барабана и наклонной плоскости
– максимальное значение коэффициента трения покоя при скорости точки касания барабана и наклонной плоскости ![]() . Так как
. Так как
![]() ,
,
То при качении без проскальзывания должно выполняться условие
![]()
3. Моделирование движения системы в случае нарушения условия качения без проскальзывания.
d=a=0.04, b=-0.1(c/м), с=1(с/м).
С началом проскальзывания система приобретает две степени свободы. В качестве обобщённых координат, описывающих движение системы, возмём углы поворота барабана и катка: ![]() ,
, ![]() .
.
Для составления дифференциальных уравнений, описывающих движение системы, используем уравнения Лагранжа второго рода:
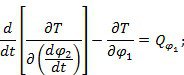
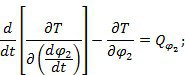
Кинетическая энергия системы:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Выразим ![]() по формулам для скоростей при плоскопараллельном движении, приняв за полюс точку B:
по формулам для скоростей при плоскопараллельном движении, приняв за полюс точку B:
![]()
![]()
![]()
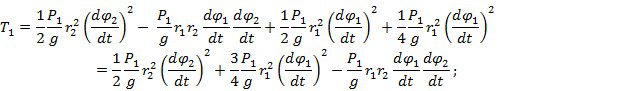
![]()
Производные от Т:
![]()
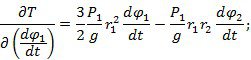
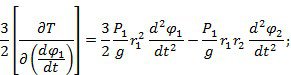
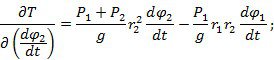
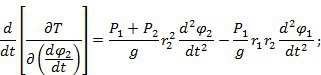
Виртуальная работа сил, приложенных к системе:
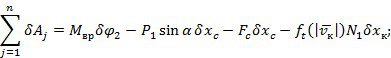
Виртуальное смещение центра масс барабана, угол поворота вала и барабана соотносятся друг с другом так же, как скорость центра масс барабана и угловые скорости барабана и вала:
![]()
Скорость точки касания катка к наклонной плоскости:
![]()
Проецируя формулу для скорости ![]() на ось, параллельную наклонной плоскости, получим модуль скорости точки проскальзывания
на ось, параллельную наклонной плоскости, получим модуль скорости точки проскальзывания
![]()
Для виртуального перемещения точки К:
![]()
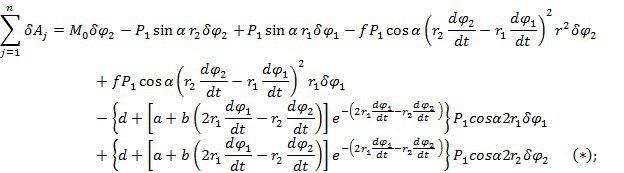
С другой стороны виртуальную работу можно выразить через обобщенные силы:
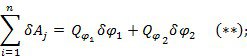
Из сравнения (*) и (**), получаем:
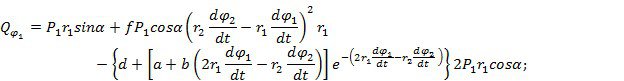
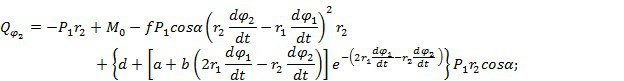
Дифференциальные уравнения движения системы:
![]()
![]()
Похожие материалы
... значениях функции. Начальное значение функции:. (2.10) Конечное значение функции: . (2.11) 7. Теорема запаздывания . (2.12) 4. Дифференциальные уравнения САУ При математическом описании систем автоматического управления составляют уравнения статики и динамики. Уравнения статики описывают установившиеся режимы и, как правило, являются алгебраическими. Уравнения динамики ...
... внутреннее строение систем, если они одинаковым образом перерабатывают информацию и оказываются эквивалентными в информационном смысле. 4. Современные тенденции развития методологии естественно-научного познания Итак, в современных естественно-научных исследованиях используются самые различные методы и методологические приемы. Следует отметить, что вопросы методологии естественнонаучного ...
... коэффициента деполяризации от концентрации. Одним из возможных путей изучения механизма светорассеяния является исследование динамики рассеяния света в импульсных электрических и магнитных полях. Схема экспериментальной установки, предназначенной для изучения процессов рассеяния света магнитной жидкостью в импульсных магнитных полях, представлена на рисунке 4. 3 2 ...
... , нужно посредством правил подсчета значащих цифр округлить результат математических вычислений так, чтобы точность их соответствовала точности данных, полученных от измерения. ИЗУЧЕНИЕ КИНЕМАТИКИ И ДИНАМИКИ ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ НА МАШИНЕ АТВУДА Цель работы Экспериментальная проверка основных уравнений и законов поступательного движения тела на специально сконструированной для этого ...
... военного оборудования. ЗАКЛЮЧЕНИЕ В результате выполнения дипломного проекта после анализа существующих конструкций автомобилей и автопоездов, общетранспортного назначения, был разработан дифференциал повышенного трения для седельного тягача с колесной формулой 4ґ2. Проведены тягово-динамический расчет, расчет дифференциала, проверочный расчет конической главной передачи. А также выполнен ...



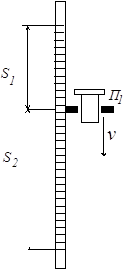
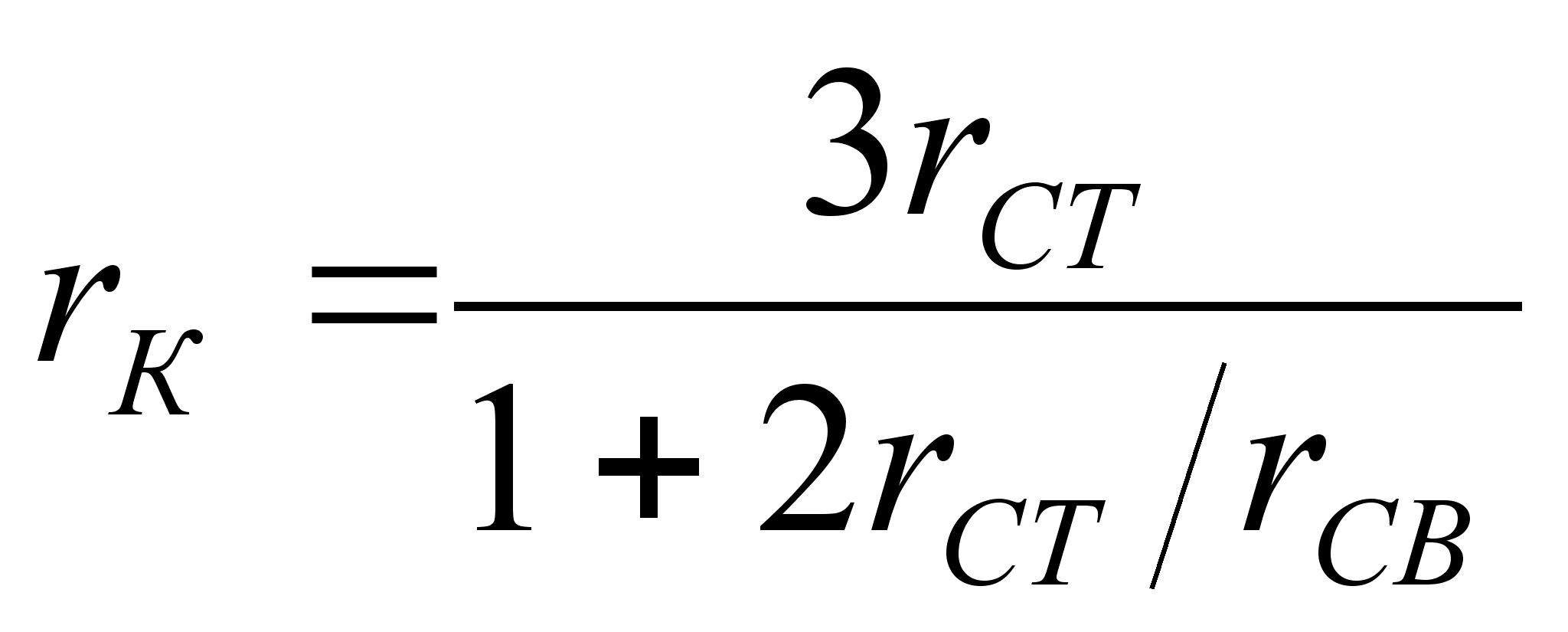
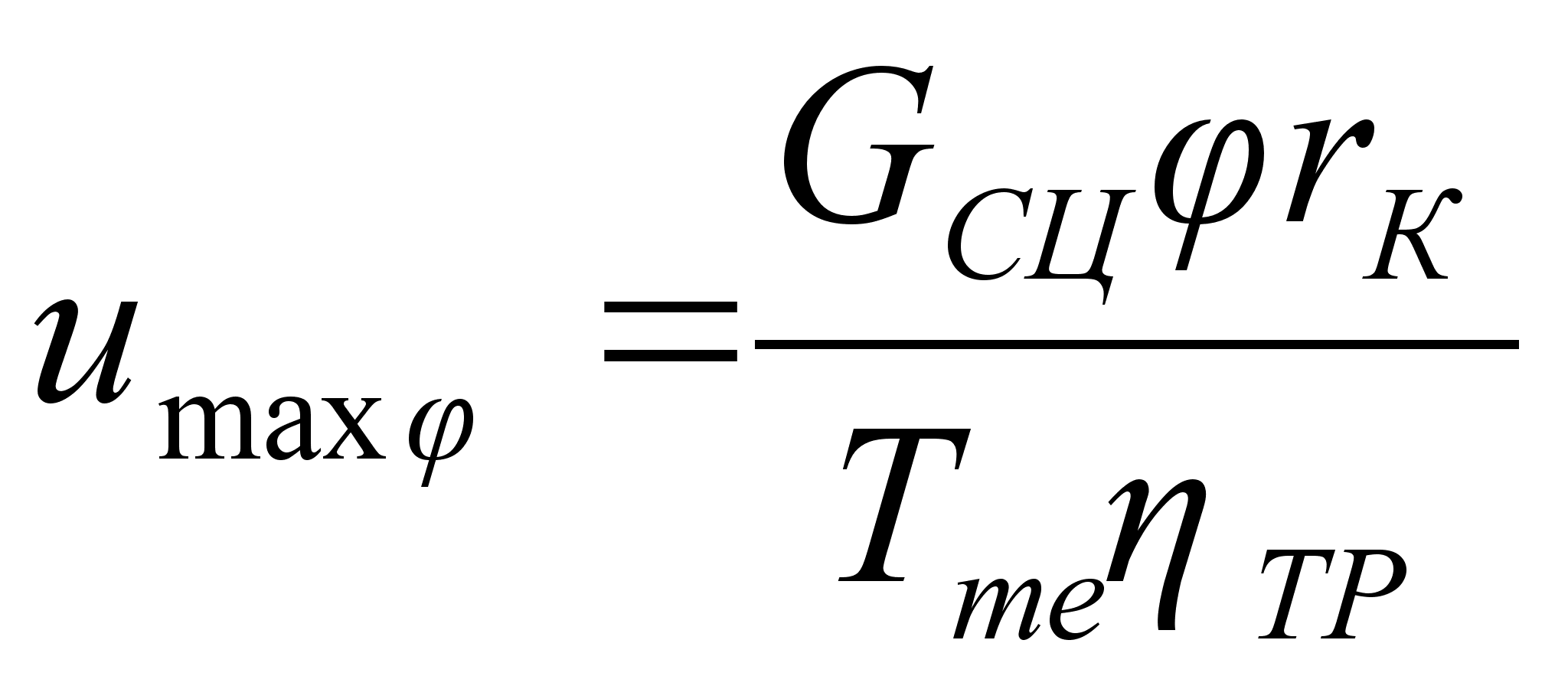
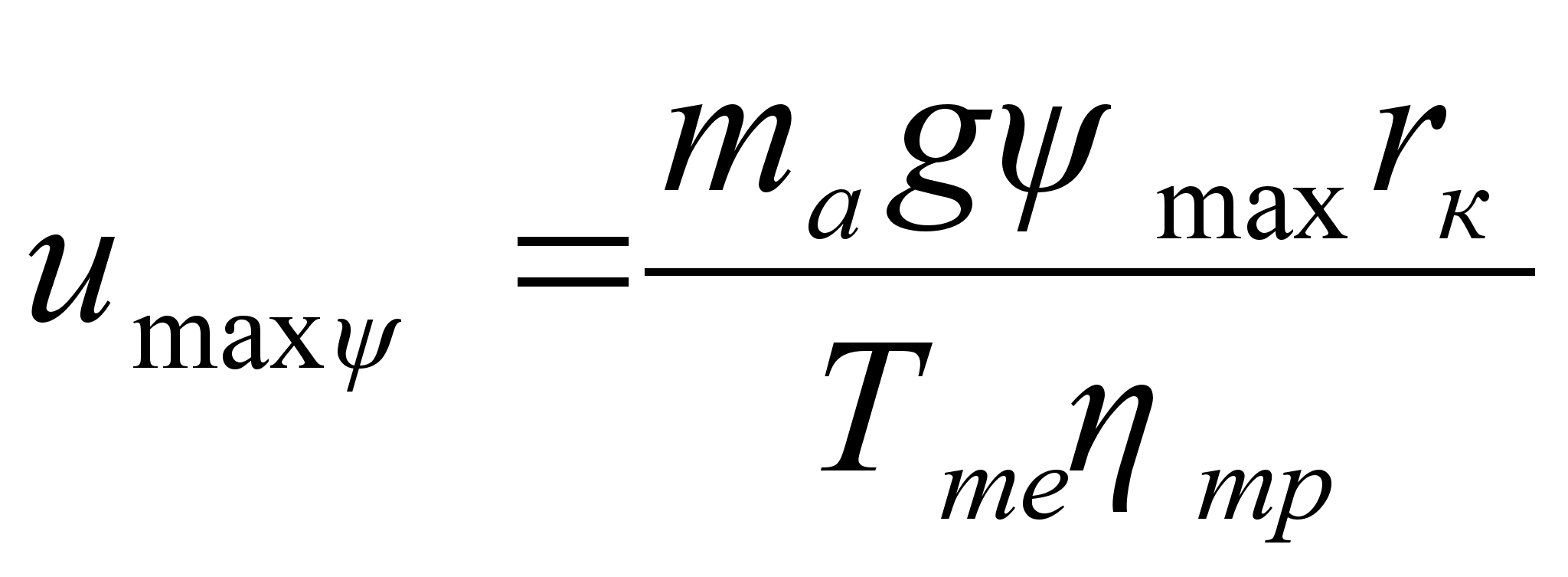
0 комментариев