Метод Мак-Кормака в вычислительной гидродинамике

ДОНЕЦКАЯ НАРОДНАЯ РЕСПУБЛИКА

ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ

КАФЕДРА АНГЛИЙСКОГО ЯЗЫКА

ДЛЯ ЕСТЕСТВЕННЫХ И ГУМАНИТАРНЫХ СПЕЦИАЛЬНОСТЕЙ

РЕФЕРАТ

ПО ПРОЧИТАННОЙ на английском языке ЛИТЕРАТУРЕ

ПО ТЕМЕ:

«Метод Мак-Кормака в вычислительной гидродинамике»

Аспиранта: Коркишко Валерии Владимировны

Специальность: 01.02.05 «Механика

жидкости, газа и плазмы»

Руководитель по специальности:

д-р тех. наук, проф. Семко А.Н.

Руководитель по англ. языку:

к. фил. наук, Захарова А. Л.

ДОНЕЦК 2016

Отзыв научного руководителя

на реферат Коркишко В.В.

«Метод Мак-Кормака в вычислительной гидродинамике»

аспиранта

Кафедры общей физики и дидактики физики

Реферат по английскому языку по прочитанной литературе В. В. Коркишко на тему «Метод Мак-Кормака в вычислительной гидродинамике» посвящен изучению перспективы применения численного метода Мак-Кормака, популярного в газодинамике и аерокосмической динамике, к задачам вычислительной гидродинамики. И газодинамика, и гидродинамика описывают процессы, происходящие в сплошных средах, но при решении задач о движении жидкости необходимо учитывать многие специфичные факторы, такие как кавитация, наличие свободной поверхности, необходимость использовать в расчетах подвижную сетку.

В своем реферате В. В. Коркишко рассмотрела литературу посвященную вопросу, подобрала примеры, демонстрирующие возможность применения метода Мак-Кормака для задач гидродинамики.

В. В. Коркишко в процессе работы проявила самостоятельность, умение творчески работать с литературой, умение ставить задачи и выбирать наилучшие способы для их решения.

Реферат заслуживает оценки «ОТЛИЧНО».

Научный руководитель Семко А.Н.

Содержание

Введение ……………………………………………………………… 3

Раздел 1. Вклад Р. Мак-Кормака в развитие вычислительной гидродинамики …………………………… 4

Раздел 2. Метод Мак-Кормака ………………………………… 8

Выводы ……………………………………………………………….. 13

Список использованной литературы ………………….... 14

Введение

Численные компьютерные симуляции сегодня являются неотъемлемой частью академического и промышленного процесса. Это явно видно по огромному количеству научных статей, появляющихся в периодических изданиях по всему миру, и по широкому разнообразию соответствующего программного обеспечения. Жидкостная динамика в этом отношении не исключение. При решении задач гидродинамики очень часто оказывается, что получить точное аналитическое решение - невозможно. Поэтому используют приближенные методы вычисления, или численные методы. Их можно разделить на два типа: методы с выделением разрывов и методы сквозного счета. Среди методов сквозного счета отдельную нишу занимают центральные схемы. Такие схемы могут служить универсальным конечно-разностным методом для решения нелинейных конвективно-диффузионных уравнений. Суть в том, что они не привязаны к специфичной собственной структуре задачи, а поэтому могут применяться напрямую как некие решающие черные ящики для общих законов сохранения и связанных с ними уравнений, управляющие спонтанно возникающими значительными градиентами.

Сейчас очень актуальным является повышение точности решения задач с помощью адаптации методов большего порядка аппроксимации.

Объект исследования – численные методы второго порядка.

Предмет исследования – метод Мак-Кормака

Цель работы: обзор современных статей о применении метода Мак-Кормака

Реферат состоит из двух разделов. Первый раздел посвящен анализу достижений Роберта Мак-Кормака в сфере компьютерного физического моделирования. Во втором разделе приведена формулировка явного метода Мак-Кормака, рассмотрена проблема численной устойчивости, принципы расширения одномернойц задачи на многомерное пргостранство.

Раздел 1. Вклад Р. Мак-Кормака в развитие вычислительной гидродинамики

Роберт Мак-Кормак – один из главных «двигателей» вычислительной динамики еще с самого момента обособления этого раздела физики, как отдельной науки. Он сделал значительный вклад в основы численных методов, применяемых для решения задач, описывающих движение сжимаемой среды, включая высокоскоростные среды с неравновесными химическими процессами. Кроме того, он применил эти методы к важным фундаментальным задачам, среди которых описание взаимодействия между пограничными слоями ударной волны, сверхзвуковые потоки для compression ramps, а также решил некоторые чисто прикладные задачи, например, обтекание аэрокосмических приборов.

Большинство исследователей, работающих в сфере вычислительной гидродинамики, хорошо знакомы с чрезвычайно эффективной модификацией метода Лакса-Вендроффа, известной в литературе как «метод Мак-Кормака». Но вместе с тем немало важных положений и идей Мак-Кормака касательно численных расчетов в газовой и гидродинамике остаются мало изученными. К таким концепциям относятся: конечно-объемный метод Мак-Кормака, метод с использованием численной диссипации второго и четвертого порядка, неявная схема Мак-Кормака, использование релаксационных техник для итерации уравнений сжимаемой среды в устойчивом состоянии и его модифицированная приближенная факторизованная схема. Он также использовал под-итерацию для ограничения (или минимизации) ошибок расщепления, обосновал применение численной вязкости в форме, подобной к форме естественной вязкости, для сохранения конструкции решений уравнений Навье-Стокса.

Мак-Кормак применил свои идеи ко многим физическим проблемам, включая задачи о сверхзвуковых ламинарных и турбулентных течениях и течениях с температурной или химической неравновесностью. Также он работал в сфере магнитогидродинамики.

Первая работа Роберта Мак-Кормака проводилась на базе исследований NASA и касалась гиперзвуковых ударных волн. Его статья обобщала эксперименты, которые проводились для решения такой задачи: «Нужна ли газообразная атмосфера для вспышек видимого излучения при гиперзвуковом бомбардировании. Эти эксперименты имели целью определить химический состав лунной поверхности с помощью спектрографического анализа при гиперзвуковой бомбардировании темной стороны луны.

Анализ энергий, необходимых для протекания различных процессов, приводящих ко вспышке, показал что зависимость наблюдаемых величин уровня яркости от окружающего давления, была величиной постоянной с учетом взаимодействия быстродействующего возмущения с атмосферой – именно это и было основной причиной излучения. В своей статье Роберт Мак-Кормак отметил, что для более высоких скоростей, или для других материалов, кроме алюминия и базальта, на которых проводилось тестирование, механизм образования выемок может оказаться достаточным условием для возникновения видимого излучения.

Было необходимо решить проблему численно, даже для облегченного, осесимметричного случая, и численное решение этой задачи было получено Робертом Мак-Кормаком с помощью схемы второго порядка точности. Эта схема получилась из схемы Лакса-Вендроффа путем введения предиктора и корректора: 1) предиктор рассчитывался с помощью разностного дифференцирования в направлении «назад», а корректор – «вперед». С тех пор придуманная им схема стала очень популярна в вычислительной гидродинамике, и носит название хемы Мак-Кормака. В статье Мак-Кормак изучает устойчивость схемы и доказывает, что применение обратных направлений при дифференцировании предиктора и корректора позволяет значительно уменьшить временной шаг и, тем самым, повысить точность решения. Это предположение не единожды проверялось на практике при применении метода Мак-Кормака для разнообразных задач.

Сложное взаимодействие, которое возникает, когда ударная волна падает на ламинарный пограничный слой, была проблемой, которую выбрал Роберт Мак-Кормак для демонстрации своего метода. Там, где другие исследователи численных методов пытались справиться и не смогли достичь успеха, именно Мак-Кормаку удалось численно решить уравнений Навье-Стокса для сжимаемой жидкости.

Причины успеха Роберта были "очевидны", как любят говорить математики. Во-первых, метод был прост. Во-вторых, он расщеплялся по времени до двух одномерных операторов, при этом сохраняя второй порядок точности. В-третьих, произошло также расщепление вычислительной области на внутренний и внешний вязкие домен, что позволило использовать для них различные формулы и тем самым повысить точность решения. В-четвертых, что было оценено меньше всего, наклонная техника дифференцирования была применена для расширенных областей и был применен подход с обеспечением четвертого порядка точности с одновременным сглаживанием колебаний функции. Главным было то, что эти подходы были так «спаяны», что схемы оставалась устойчивой при стремление параметра устойчивости к единице.

Метод Мак-Кормака с расщеплением по времени так «расщепляет» оригинальную схему Мак-Кормака, что решение многомерной задачи сводится к последовательному решению одномерных задач. Благодаря этому условие устойчивости разностной схемы становится менее жестким. Другими словами, расщепление позволяет получить решение в каждом направлении с максимально допустимым шагом по времени. Особенно заметно преимущество расщепления в том частном случае, когда максимально допустимые шаги по времени, сильно отличаются друг от друга из-за различия пространственных шагов разностной сетки.

Мак-Кормак сделал огромный вклад в вычислительную гидродинамику еще и тем, что сформулировал принцип контрольного объема для достижения консервативной формы уравнений. Вместо того чтобы вычислять разности непосредственно из управляющих дифференциальных уравнений, он пришел к выводу, что поток жидкости может быть локально разделен на контролируемые конечные объемы (или ячейки). При этом силы, действующие в жидкости, оказывают действующими на границы ячеек, а масса, момент движения и энергия – транспортируются сквозь ячейку. Эта концепция была благоприятно воспринята исследователями в области вычислительной гидродинамики и сейчас широко применяется при решении задач. Методы, используемые в этой ветви вычислительной гидродинамики так и называются: «конечно-объемные схемы».

Из-за значительных ограничений на временной шаг для явного метода, в конце 70-х годов стали активно разрабатываться неявные, способные увеличить точность решения. Также стали предметом глубокого изучения такие идеи, как расщепление потока, противо-потоковое дифференцирование, методы с уменьшением суммарной вариации параметров. В 1981 году Мак-Кормак ввел бидиагональную неявную разностную схему Мак-кормака, которая опиралась на подход предиктор-корректор.

В своей статье Мак-Кормак установил очень важную концепцию для развития численных методов, применяемых для вычисления параметров устойчивого состояния. Он предположил, что желательной формой численного метода является запись через дельта-форму, при которой числовые параметры оказываются с одной стороны, например, слева от знака равно, а точные аппроксимации физического уравнения – с другой, например, правой. Задачей левой (числовой) части является создание локально определенного решения, которые в остается устойчивым без значительно урезания законов физики.

Для численной эффективности лево-сторонние элементы должны быть максимально удобными и легко применимыми. Они также должны приводить параметры правой стороны к нулю с наибольшей скоростью. Дельта-форма была представлена еще ранее, в работах Бима и Варминг, описывающих его явный метод. Однако именно Мак-Кормак сделал такую схему вычислительной гидродинамики, которая была бы понятной и с легко прослеживаемой логикой расчета. Он, как и раньше, локально расщеплял уравнения Навье-Стокса на одномерные операторы. Разности вперед и назад применялись к линеаризированным матрицам потоковых величин в явных операторах. Разности с направлением «вперед» для шага предиктора и с направлением «назад» для корректора вылились в простую бигональную матрицу инверсных параметров для явной процедуры. Сочетание двух (предиктор и корректор) бидиагональных скалярных матриц создает, и довольно эффективно, диагональный доминирующий оператор матрицы.

После добавления явной процедуры, метод теоретически стал устойчивым для любого временного шага. Он более не нуждался ни в скалярных, ни в смешанных тридиагональных матрицах инверсий параметров. Таким образом, метод стал более эффективным и была достигнута более высокая скорость расчетов.

Раздел 2. Метод Мак-Кормака

Метод Мак-Кормака – это конечно-разностный метод типа предиктор-корректор. Метод Мак-Кормака широко используется для решения задач движения сжимаемого потока и других задач последние 30 лет. С момента появления схема Ма-Кормака претерпела множество модификаций и обобщений. Существуют как явная, так и неявная версии этого алгоритма. Также развита модификация для применения в методе конечных объемов. Метод Мак-Кормака считается краеугольным камнем вычислительной гидродинамики. Как явная, так и неявная версии метода позволяют решать гиперболические и параболические уравнения для положительного временного шага, при этом проявляя хорошие диссипативные и дисперсионные краевые свойства.

Популярность явного метода Мак-Кормака обусловлена как простотой его выражений, так и простотой применения этого метода, в том числе и для многомерных задач. Этапы предиктора и корректора используют прямое дифференцирование для производных по времени первого порядка, и одностороннее дифференцирование пространственной производной первого порядка. (Bernard., 1992) Для предиктора и корректора при дифференцировании по времени используется только разности «вперед». А вот направления пространственного дифференцирования в предикторе и корректоре всегда противоположны. В примере, если в схеме на шаге предиктор используются разности «назад», то в корректоре – «вперед». Разности «назад» и «вперед» можно циклически чередовать: таким образом, устраняется рассогласование, обусловленное аппроксимацией односторонними разностями, благодаря чему при вычислении нет нужды в расчете Якобиана, как это происходит в одно-шаговой явной схеме типа Лакса-Вендроффа

Основой метода Лакса-Вендроффа является разложение в ряд Тейлора до слагаемого второго порядка, где напрямую вычисляется из частных дифференциальных уравнений и – определяется дифференцированием частных дифференциальных уравнений по времени.

Мак-Кормак предложил альтернативных подход к оцениванию , который опирается на разложение в ряд Тейлора первого порядка точности с дифференцированием по времени вперед для от исходной точки (i,n).

Т.е.

=+

Решив уравнение для получим

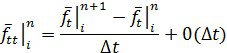
В итоге получим

=

Используя свойства частных дифференциальных уравнений, проведем замену и тогда уравнение примет форму

=

Заменяя и центрально-разностными аппроксимациями второго порядка точности и отбросив остаточные члены уравнения, получаем функциональное дифференциальное уравнение с порядком точности . Разностная расчетная сетка представлена на рис.2.1.

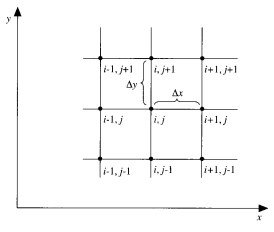
Рис.2.1. Прямоугольная расчетная сетка

Такая замена приводит к неявному функциональному дифференциальному уравнению, которое крайне сложно решить в рамках нелинейных частных дифференциальных уравнений.

Мак-Кормак предложил процедуру предиктор-корректор, которая расчитывает спрогнозированные величины , используя аппроксимации первого порядка с разностями «вперед» для величин и , и таким образом получается:

= ,

где – параметр конвекции (в данном случае, число Куранта). На следующем шаге (корректора) уравнение решается оцениванием через аппроксимацию первого порядка в направлении «вперед» уравнения и оцениванием через аппроксимацию первого порядка в направлении «назад», базируясь на уже просчитанных величинах :

=

Проведя некоторые преобразования, получим формулу более пригодную для компьютерного расчета:

=

Уравнения описывают приближение методом Мак-Кормака для линейного конвективного уравнения. Шаблон аппроксимация представлен на рис.2.2.

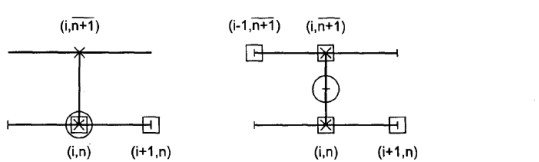
Рис.2.2. Шаблон метода Мак-Кормака

Метод Мак-Кормака использует аппроксимацию разностями «вперед» для и аппроксимацию разностями «назад» для . Эти разности могут применяться и в обратном порядке. В противном случае в решении возникает несогласованность из-за применения односторонних разностей. Если есть желание, то эта несогласованность может быть ослаблена применением альтернативно направленных пространственных производных в предикторе и корректоре на каждом временном шаге. Свойства метода Мак-Кормака не очевидны из уравнений. Устреднение по времени пространственных производных в корректоре, определяет порядок аппроксимации равным . Однако при более глубоком рассмотрении ошибки дискретизации, порядок точности для метода Мак-Кормака оказывается равным .

Метод Мак-Кормака при первом рассмотрении кажется ничем иным, как одно-шаговым методом Лакса-Вендроффа. Однако они идентичны только для линейных конвективных уравнений. Для нелинейных частных дифференциальных уравнений и систем нелинейных частных дифференциальных уравнений эти два метода похоже ведут себя, но дают не идентичные решения. При этом для двух- и трехмерных пространств метод Мак-Кормака более эффективен, чем метод Лакса-Вендрофа.

Так как для линейных конвективных уравнений метод Мак-Кормака идентичен методу Лакса-Вендроффа, то и анализы устойчивости и точности решению дают сходные с методом Лакса-Вендроффа результаты. Таким образом, метод дают решение с порядком точности + , устойчив при выполнении условия и конвергентен.

Для равномерных сеток схема Лакса-Вендроффа, а значит и схема Мак-Кормака имеет второй порядок аппроксимации по времени и пространству на гладких решениях. При сквозном счете скачков (разрывных решений) она дает заброс и затухающие колебания решения за фронтом движущегося разрыва, то есть является немонотонной. Контактные разрывы эта схема размазывает только за счет физической вязкости, что является ее достоинством. Немонотонность схемы Лакса-Вендроффа для задач упругопластического деформирования приводит к дополнительным ошибкам в расчете истории напряженно-деформированного состояния из-за нефизических смен режимов нагружение-разгрузка за ударными волнами. Поэтому для исключения таких ошибок ее используют совместно с какими-либо процедурами дополнительной монотонизации решений, которые рассматриваются далее. Подчеркнем также необходимость обеспечения консервативности для сходимости результатов сквозного счета разрывных решений.

В отличие от схемы Лакса Вендроффа вместо осреднения Лакса на предикторе и центральных разностей здесь для стабилизации применены односторонние разности и на предикторе, и на корректоре, но в разные стороны. То есть на одном из таких

полушагов схема заведомо неустойчива, а на другом – наоборот обладает избыточным запасом устойчивости. В сумме двух шагов получается устойчивая для линейных уравнений схема второго порядка точности. Как и в схеме Лакса-Вендроффа диффузионный оператор учитывается только на корректоре по обычной центрально-разностной схеме.

Следует отметить, что в нелинейных задачах газовой динамики схема Мак-Кормака локально неустойчива в сверхзвуковых зонах разрежения и в дозвуковых зонах возвратно-циркуляционного течения. Как и схема Лакса-Вендроффа схема Мак-Кормака немонотонна. Введением монотонизаторов ее можно заставить работать устойчиво. Отметим, что эквивалентная по дифференциальным приближениям схема с центрально-разностной аппроксимацией содержит дополнительную искусственную вязкость на предикторе и корректоре с альтернирующим по знаку коэффициентом искусственной вязкости ± | U | / 2 h . Это означает, что на одном из шагов вводится дополнительная диффузия, а на другом – антидиффузия.

Выводы

Метод Мак-Кормака дает исследователям в области гидродинамики очень удобный инструментарий для решения уравнений движения сжимаемой и несжимаемой жидкости, в том числе для решения уравнений Ейлера и Навье-Стокса. Простота применения метода Мак-Кормака, высокая эффективность и точность решения являются очень важными свойствами данного численного метода. Благодаря применению процедуры предиктор-корректор метод становится легко применяемым для компьютерного расчета, даже при обобщении одномерной задачи на двумерный и трехмерный случаи. Метод Мак-Кормака также является хорошей, твердой базой для создания численных модификаций четвертого порядка точности и выше.

Метод Мак-Кормака также проявляет высокие свойства стабильности. В этом отношении метод Мак-Кормака повторяет метод Лакса-Вендроффа и дает те же условия устойчивости. Для одномерного случая, параметром устойчивости выступает число Куранта и связанные с ним величины.

Список использованной литературы

1. Bernard Robert. – A MacCormack scheme for incompressible flow. – Computers Math. Applic. Vol.24. No. 5/6. 1992 – pp. 151 – 168.

2. Caughey, Hafez. Contributions of Robert Mac-Cormack to Computational Fluid Dynamics, in: Frontiers of Computational Fluid Dynamics 2002, Caughey, Hafez (ed); p.1-26, London, World Scientific Publishing Co, 2002.

3. Gottlieb David. Dissipative Two-Four Methods for Time-Dependent Problems. – Mathematics of computation, Vol.30, No. 136, 1976. – pp. 703-723

4. Griffiths Davis, Higham Desmond. MacCormack’s method for Advection-Reaction Equations. – University of Strathclyde Mathematics Research Report, No.25. 1999.

5. Griffiths Davis, Higham Desmond. Runge Kutta and MacCormack’s dynamics. – University of Strathclyde Mathematics Research Report, No.18. 1999.

6. Hoffman J. D. Numerical methods for engineers and scientists. Second edition revised and expanded. – New York: Marcel Dekker, Inc. – 2001. – pp. 651 – 701.

7. Anderson J. D. Journal of Computational fluid dynamics: the basics with application. / McGraw-Hill Series in Mechanical Engineering. – New York: McGraw-Hill, Inc. – 1995. – pp. 216 – 280.

8. Kurganov A. Tadmor E. New High-Resolution Central Schemes for Nonlinear Conservation Laws and Convection–Diffusion Equations. – Journal of Computational Physics 160, 2000. – 241–282 p.

9. Bram V. Upwind and High-Resolution Methods for Compressible Flow: From Donor Cell to Residual-Distribution Schemes. - Communications in computational physics. Vol. 1, No. 2, 2006. – pp. 192-206.

10. MacCormack R.W. Numerical Solution of the Interaction of a Shock Wave with a Laminar Boundary Layer, in: Proceedings of the Second International Conference on Numerical Methods in Fluid Dynamics, Lecture Notes in Physics, Holt M. (ed.) vol. 8, p.151-163, New York, Springer-Verlag, 1971.

11. MacCormack R.W. Viscosity Effects in Hypervelocity Impact Cavering, in: Frontiers of Computational Fluid Dynamics 2002, Caughey, Hafez (ed); p.1-26, London, World Scientific Publishing Co, 2002.

12. Wendroff Burton. The stability of MacCormack’s method for the Scalar Advection Equation. – Appl. Math. Lett., Vol.4., No. 2, 1992 – pp. 89-91.

13. Zalesak Steven. Fully Multidimensional Flux-Corrected Transport Algorithms for Fluids (Naval Research Laboratory, Washington). – Journal of Computational Physics, 31, 1979. – 335-362 p.

SUMMARY

The numerical scheme for the computation of a shock discontinuity developed by MacCormack has been extended to solve a number of differential equations, including cases explicitly containing higher-order derivatives. Comparisons with previous results are made, if available, to illustrate the advantages of the present method. The question of convergence of the numerical calculation is discussed. In the paper the author analyzes the stability of the scheme when the backward/forward steps are applied. Such principle will allow the full (one-dimensional) CFL limit on time step. This conjecture certainly has been verified again and again in numerous applications of the method, but has not been proved.

The authors suggest a positive correlation between the accuracy and efficiency of a numerical method, pointing out that an explicit scheme operating at its maximum allowable time step has all the data needed to advance the solution, with a minimum of extraneous data. The purpose of this paper is to demonstrate the advantages of MacCormack scheme used earlier for the shock wave/laminar boundary layer interaction problem to more general fluid dynamics problems. The split explicit MacCormack scheme is applied to the inviscid equations of compressible flow to solve for the supersonic flow past symmetric diamond-shaped airfoils and double compression corners using simple, non-orthogonal, sheared meshes. They achieve results in excellent agreement with the exact (inviscid) solutions for these problems, demonstrating a reduction in computational time of more than a factor of two, relative to the unsplit method. The split method allows both: 1) advancing the solution at the full one-dimensional CFL limit in each space dimension, and 2) advancing the solution in the direction of the smaller mesh spacing multiple time steps for each time step in the coarser direction, allowing a better matching of the numerical and physical domains of dependence.

The authors use three problems to illustrate three different points. The linear wave (advection) equation is used to show that the MacCormack explicit method reproduces the exact solution at a Courant number of unity due, the authors argue, to the alignment of the spacetime mesh with the solution for this value of Courant number. Second, the inviscid Burgers equation is used to show that, without corrective measures, the numerical scheme may capture (physically incorrect) expansion "shocks." Finally, the authors consider solutions of the Euler equations for several two-dimensional, supersonic flows, including flows past wedges, diamond airfoils, and a sphere. For these flows it is shown that the numerical error is reduced when the mesh is aligned with the shock position.

Список терминов

1	Advective	Адвективный В гидродинамической литературе на русском языке примерно до 2010 года термин переводился как «конвективный», т.е. термины аdvective и сonvective не различались. В работах после 2010 термины различаются только при переводах статей с английского языка.
2	Artificial viscosity	Искусственная вязкость
3	Basin	Базис шаблона
4	Cavity	Кавитация
5	Cell-centered algorithm	Алгоритм, опирающийся на данные центра ячейки
6	Characteritic decompositions	Характеристическое разложение
7	Componentwise approach	Компонентный подход
8	Computational Fluid Dynamics (CFD)	Вычислительная гидродинамика
9	Conservation form	Консервативная форма
10	Conservation law	Закон сохранения
11	Conserved variables	Консервативные члены
12	Consistency	Cогласованность
13	Convection number	Параметр конвекции
14	Convection-diffusion	Конвективно-диффузионный
15	Convective	Конвективный
16	Convergence	Cходимость
17	Convex	Выпуклый
18	Curvature	Кривизна
19	Curvilinear coordinate	Криволинейные координаты
20	Degenerate diffusion	Вырожденная диффузия
21	Density	Плотность
22	Discrete	Дискретный
23	Dispersive ripples	Дисперсионные осцилляции
24	Dissipation lenght	Ширина «размазывания»
25	Eigenstructure	Собственная структура
26	Eigenvalue	Собственные значения
27	Explicit	Явный
28	Face-centered algorithm	Алгоритм, опирающийся на параметры границ
29	Family of schemes	Семейство схем
30	FCT (Flux-Corrected Transport)	Техника с корректированием потоков в ячейке
31	FDE (functional differential equation)	Функциональное дифференциальное уравнение
32	Finite-difference method	Конечно-разностный метод
33	Fluid dynamics	Гидродинамика
34	Flux	Поток
35	Forward-difference approximation	Аппроксимация разностями «вперед»
36	Framework	Структура
37	Heat conductivity	Теплопроводность
38	Hypersonic	Ультразвуковой
39	Hypervelocity	Гиперзвуковая (космическая) скорость
40	Impact cratering	Образование кратера ударной волной
41	Implicit	Неявный
42	Incompressible	Несжимаемый
43	Initial value	Начальные параметры
44	Interface	Сопряжение
45	Interpolant	Интерполированный
46	Inviscid	Невязкий
47	Irrotational	Невихревой
48	Laminar	Ламинарный
49	Maximum principle	Принцип максимума
50	Mesh ratio	Параметр сетки
51	Minmod limiter	Ограничитель типа minmod
52	Multidimensional	Многомерный
53	Node	Узел ячейки
54	Non-equilibrium	Неравновесный
55	Nonoscillatory	Монотонный
56	Nonsmooth	Негладкий
57	Numerical viscosity	Численная вязкость
58	ODE (ordinary differential equation)	Обыкновенное дифференциальное уравнение
59	One-dimensional	Одномерный
60	One-side approximation	Одно-сторонняя аппроксимация
61	Order of accuracy	Порядок точности
62	PDE (Partial Differential Equation)	Частные дифференциальные уравнения
63	Piecewise-linear approach	Кусочно-линейный подход
64	Plate wave	Плоская волна
65	Pressure	Давление
66	Propagation speed	Скорость переноса
67	Relative error	Относительная ошибка
68	Relaxation scheme	Релаксационная схема
69	Resolution	Разрешающая способность
70	Riemann fans	Области Риманового решения
71	Round-off error	Ошибка округления
72	Semi-discrete	Полу-дискретный
73	Shock discontinuities	Разрыв
74	Skin friction	Поверхностное трение
75	Smooth	Гладкий
76	Source term	Параметр истока
77	Space derivative	Производная по координате
78	Space marching	Пространственная дискретизация
79	Spatial	Пространственный
80	Stability	Устойчивость
81	Steady state	Устойчивая фаза
82	Stencil	Шаблон
83	Streamline	Линия тока
84	Stress term	Параметр напряжений
85	Supersonic	Сверхзвуковой
86	Taylor expansion	Разложение в ряд Тейлора
87	Temperatute	Температура
88	Temporal	Временной
89	Time averaging	Усреднение по времени
90	Time derivative	Производная по времени
91	Time marching	Временная дискретизация
92	Total-variation diminishing method (TVD)	Метод с устремлением общей вариации параметра к минимуму
93	Transonic	Трансзвуковой
94	Transportive flux	Транспортный поток
95	Truncation error	Ошибка дискретизации
96	Turbulent	Турбулентный
97	Two-dimensional	Двумерный
98	Upwind scheme	Схемы, с расчетом параметра в направлении «против потока»
99	Vortex	Вихрь
100	Weak condition	Условие, определяющее слабое решение

My research

My name is Valeria Korkishko. I graduated from Donetsk National University in 2014. Now I’m a post-graduate student of the Faculty of Physics and Technology. I’m a teacher of physics. I really love my job, I love the process of sharing my knowledge with other people. But I also have interests in science. My special subject is Computational Fluid Dynamics. My research deals with principals of modeling pulse and wave flows with mobile borders.

I’m particularly interested in application of Mac-Cormack method to the high pulse fluid flows. One of the first tasks is to verify and if possible to amplify knowledge of possibility of application Mac-Cormack method to hydrodynamics method. I have been working at the problem for two years. I got interested in it when I was a student. My present work is based on the theory developed by my scientific adviser Alexandr Nikolaevich Semko. He has PHD at technical sciences. The title of his doctor’s dissertation was “Pulse and wave flows of liquid with mobile borders”. He proved it in 2006. Ten years after the problem hasn’t lost its topical significance.

The title of my future dissertation is “Computational modeling of high pulse processes and technologies”. Pulse and wave flows with mobile borders meet in many physical processes bound to short-term and intensive influence on fluid, such as impact, explosion, electrical discharge etc. Dimensional redistribution of energy takes place in such kind of processes. It leads to sharp local increase of energy density. This effect is widely used in different installations and technological processes. Essential features of such processes are fugacity, high pressure, wave character and cavitation. Such flows are described by equations of non-stationary gas dynamics with appropriate initial and boundary conditions. Boundary conditions are often put on the specific borders. Motion laws of such borders are not known in advance and are a part of the decision of a problem.

All these factors essentially complicate the decision of such issues. Therefore working out of the mathematical models adequately reflecting pulse and wave flows of fluid with mobile borders and cavitation is still the actual problem to which my research is devoted.

Computational Fluid Dynamics (CFD) provides a qualitative (and sometimes even quantitative) prediction of fluid flows by means of mathematical modeling (partial differential equations), numerical methods (discretization and solution techniques) and software tools (solvers, pre- and post-processing utilities). CFD uses a computer to solve the mathematical equations for the problem at hand. At present there is a growing interest in improving the accuracy of numerical methods. CFD is a highly interdisciplinary research area, which lies at the interface of physics, applied mathematics and computer science.

In computational fluid dynamics, the Mac-Cormack method is a widely used discretization scheme for the numerical solution of hyperbolic partial differential equations. This second-order finite difference method was introduced by Robert W. Mac-Cormack in 1969. The Mac-Cormack method is very elegant and easy to understand and program. It is well suited for nonlinear equations (inviscid Burgers equation, Euler equations, etc.) Unlike first-order upwind scheme, the Mac-Cormack does not introduce diffusive errors in the solution. However, it is known to introduce dispersive errors in the region where the gradient is high. In my research the theory of flux-corrected transport (FCT) developed by Boris and Book is extended to the numerical Mac-Cormack method in order to minimize dispersive errors. It has been established by recent studies that Mac-Cormacks method can be adequately applied to calculate liquid flows. So the scientific validity of my job is application of the Mac-Cormack method, widely used in gas dynamics, to liquid dynamics.

My research is based on several steps. Initially, one must make mathematical model. Secondly, generation of cells, time instants, space and time discretization comes. Main part is software implementation and post-processing visualization. And after verification of model, the certain issues can be solved. Now I got more results in theoretical part rather than in practical use of obtained data. The obtained results agree with the previous findings. The problems are still far from being completely understood.

I plan to finish my research work by the end of my study at the post-graduate course. I hope to get the degree of Candidate of Technical Science. By this time I will have got some publications in scientific periodicals. I think my dissertation will make a certain contribution to the knowledge of the subject by the discovery of new facts about the effectivity of Mac-Cormack’s method being applied to high pulse flows with mobile borders.