Правила терминов простого категорического силлогизма
Первое правило - в силлогизме должно быть только три термина (меньший, больший, средний).
Второе правило - термин, не распределенный в посылках, не может быть распределен и в заключении.
Третье правило - средний термин должен быть распределен, т.е. взят в полном объеме, хотя бы в одной из посылок.
Правила посылок простого категорического силлогизма:
Первое правило - из двух частных посылок нельзя сделать заключение.
Второе правило - если одна из посылок частная, то и заключение должно быть частным.
Третье правило - из двух отрицательных посылок заключения сделать нельзя.
Четвертое правило - если одна из посылок отрицательная, то и заключение должно быть отрицательным
Факт неправильности силлогизма можно также обнаружить посредством установления, что несоблюдены какие-то правила фигур силлогизмов.
Фигуры силлогизмов - это типы силлогизмов, выделяемые на основе способов расположения терминов в посылках.
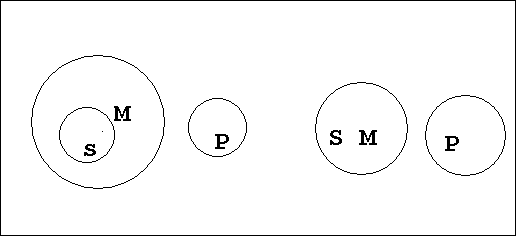
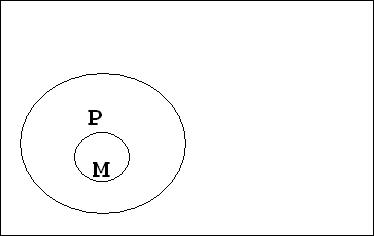
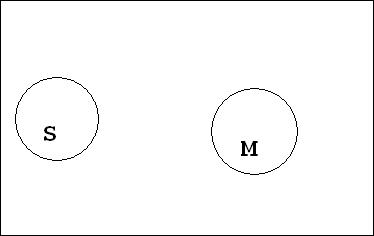
Простые категорические силлогизмы отличаются по положению среднего термина (М) в суждениях-посылках: он может стоять на месте субъекта или предиката.
С учетом этого все многообразие категорических силлогизмов сводится к четырем фигурам, каждая из которых отличается качеством и количеством посылок и заключения, т.е. модусами.
Различное местоположение среднего термина (М) можно выразить в виде схем-фигур силлогизмов
Рассмотрим их более подробно.
Первая фигура категорического силлогизма.
M P S M S P
Знамя части (М) - святыня (Р)
Это (S) - знамя части (М)
Это (S) - святыня (Р)
Первая фигура силлогизма имеет четыре модуса:
ААА (Barbara)(А) Все М есть Р(А) Все есть М(А) Все есть Р
ЕАЕ (Celarent) -(Е) Ни одно М не есть Р(А) Все есть М(Е) Ни одно не есть Р
AJJ (Darii) -(А) Все М есть Р(J) Некоторые S есть М(J) Некоторые S есть Р
EJO (Ferio) -(Е) Ни одно М не есть Р(J) Некоторые S есть М(О) Некоторые S не есть Р 2. В каждом модусе первая буква обозначает большую посылку, вторая - меньшую, а третья буква обозначает заключение.А - общеутвердительное суждение(Все S есть Р)Е - общеотрицательное суждение(Ни одно S не есть Р)J - частноутвердительное суждение(Некоторые S есть Р)О - частноотрицательное суждение(Некоторые S не есть Р)1. Модусы - виды силлогизма, различающиеся количественным и качественным характером посылок.
Анализ модусов первой фигуры категорического силлогизма позволяет вывести частные правила этой фигуры:
а) большая посылка должна быть общей (А, Е);
б) меньшая посылка - утвердительной (А, J).
С помощью первой фигуры мы всегда из общих положений выводим частные утверждения, прилагаем знания общих положений к частным фактам конкретной действительности.
Вторая фигура простого категорического силлогизма.
P M S M S P
Побеждает в бою (Р) не действующий по шаблону (М).
Он (S) не действует по шаблону (М)
ОН (S) побеждает в бою (Р)
Вторая фигура имеет четыре модуса:
ЕАЕ - Cesare;
АЕЕ - Camestres;
ЕJО - Festino;
АОО - Baroco.
Анализ модусов данной фигуры позволяет вывести частное правило:
а) большая посылка должна быть общей (А, Е);
б) одна из посылок - отрицательной (Е, О).
Вторая фигура категорического силлогизма служит для доказательства несоответствия конкретного случая общему положению, и поэтому утвердительные заключения здесь невозможны. Эта фигура категорического силлогизма широко применяется для критики научных статей, конкретных поступков и т.д.
Третья фигура категорического силлогизма.
M P M S S P
Все офицеры (М) - патриоты (Р)
Все офицеры (М) - люди (S)
Некоторые люди (S) - патриоты (Р)
Третья фигура имеет шесть модусов:
ААJ - Darapti;
АJJ - Felapton;
JAJ - Disamis;
EAO - Datisi;
EJO - Bocardo;
OAO - Ferison.
Частные правила этой фигуры простого категорического силлогизма формулируются следующим образом:
а) меньшая посылка должна быть утвердительной (А, J).
б) вывод должен быть частным (J, О).
При помощи третьей фигуры категорического силлогизма опровергаются общие утверждения. Третья фигура используется в тех случаях, когда надо поставить под сомнение что-то общепринятое, какое-то укоренившееся мнение о том, что все предметы какой-то группы должны обладать каким-то признаком. В науке третья фигура не имеет широкого распространения, т.к. ее выводы носят частный характер. Логическая ошибка возникает потому, что полученный частный вывод начинают считать общим положением и распространяют его на всех или все.
Четвертая фигура простого категорического силлогизма
P M M B S P
Все российские офицеры (Р) - хранители боевых традиций (М)
Все хранители боевых традиций (М) - патриоты (S).
Некоторые патриоты (S) - российские офицеры (Р)
Частные правила четвертой фигуры категорического силлогизма формулируются следующим образом:
а) если большая посылка утвердительная, то меньшая должна быть общей;
б) если одна из посылок отрицательная, то большая должна быть общей.
Четвертая фигура простого категорического силлогизма носит искусственный характер и, как правило, в обычных рассуждениях не употребляется, а преобразуется в другие фигуры категорического силлогизма.
При подготовке этой работы были использованы материалы с сайта http://www.studentu.ru
Похожие работы
... видов суждений, число возможных комбинаций посылок в каждой фигуре равно 22, т.е. 16: АА АЕ IA OA AE (EE) IE (OE) AI EI (II) (OI) AO (EO) (IO) (OO) Очевидно, в 4-х фигурах число комбинаций равно 64. Разновидности силлогизма, различающиеся количеством и качеством посылок, называются модусами простого категорического силлогизма. Однако не все модусы согласуются с ...
... affirmo - утверждаю - для двух утвердительных высказываний и из слова nego - отрицаю - для отрицательных. Фигуры категорического силлогизма Расмотрим (на примере) строение силлогизма. Каждый человек (М) - смертен (Р) Сократ (S) - человек(М) ~~~~~~~~~~~~~~~~~~~~~~~~~~~~ Сократ (S) - смертен (P) Силлогизм состоит из трех категорических ...
... в жизни. По схеме четвертой фигуры построен силлогизм: Все рыбы (Р) плавают (М). Все плавающие (М) живут в воде (S). Некоторые живущие в воде – рыбы. Посылками и заключениями силлогизмов могут быть категорические суждения четырех видов: SaP, SiP, SeP и SoP. Модусами силлогизма называются разновидности фигур, отличающиеся характером посылок и заключения. Всего с точки зрения всевозможных ...
... (P) предусматривает ответственность за поступки (M). Доброта (S) не требует ответственности (M) Доброта (S) несправедлива (P). Положение среднего термина определяет четыре типа построения (фигуры) простого категорического силлогизма, каждый из которых должен соответствовать своему формальному правилу вывода: Большая посылка должна быть более общей, меньшая утвердительной. Ее формула ( ...
0 комментариев