Схема размерной цепи приведена на рис. 7

6.1.2. Схема размерной цепи приведена на рис. 7.

Рис 7.

Номинальные размеры звеньев, мм:

В1=157, В2=56, В3=12, В4=36, В5=13, В6=25, В7=5 мм.

В1 – увеличивающее звено, остальные – уменьщаюшие.

6.2. Расчет.

Замыкающее звено рассчитывается по формуле:

Вå=B1–( B2+ B3+ B4+ B5+ B6+ B7),

Bå=157–(56+12+36+13+25+5)=10 мм.

Максимальный размер замыкающего звена [Bå MAX ]:

[Bå MAX ]=0.4 мм.

Минимальный размер замыкающего звена [Bå MIN ]:

[Bå MIN ]=–0.4 мм.

Предельный зазор:

,

[Så]=0.4 мм.

Предельный натяг:

,

[Nå]=–0.4 мм.

Среднее отклонение:

,

[=0.

6.2.1. Метод полной взаимозаменяемости

Предполагаем, что подшипник, являющийся стандартным изделием, уже имеет определенный квалитет и размер Т4=36–0.3.

Согласно [1], табл. 3.3., получаем количество единиц допуска для каждого из размеров, мкм:

i1=2.52;

i2=1.86;

i3=1.08;

i5=1.08;

i6=1.31;

i7=0.73.

Рассчитаем количество единиц допуска для квалитета звеньев, составляющих данную размерную цепь:

,

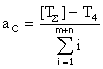где m+n – количество всех звеньев в цепи.

53 ед.

Ближайший подходящий квалитет IT10 – по табл. 1.8.

Соответствующие допуски для каждого звена, мкм:

ТВ1=185;

ТВ2=120;

ТВ3=70;

ТВ4=300;

ТВ5=70;

ТВ6=84;

ТВ7=48.

Тå=TB1+ TB2+ TB3+ TB4+ TB5+ TB6+ TB7,

Тå=185+120+70+300+70+84+48=877 мкм.

Проверка показывает: Тå=877>[Тå] – надо назначить для звеньев В1 и В7 более низкий IT9. Допуски, мкм:

ТВ1=115, ТВ7=30.

Тå=115+120+70+70+84+48=789 мкм.

Проверка: Тå=789 £ [Тå] – верно.

Назначим предельные отклонения на остальные звенья цепи, исходя из уравнения, мм:

,

где –суммарное среднее отклонение поля допуска;

С УМ – среднее отклонение поля допуска уменьшающих звеньев;

С УВ – среднее отклонение поля допуска увеличивающих звеньев;

В1=157e8=;

В2=56js9=;

В3=12js9=;

В4=36 –0.3 ;

В5=13 js9=;

В6=25js9=;

В7=5u8=.

[=­–0.1165 мм;

=0.032 мм.

Учитываем, что поле допуска js имеет =0,

,

 мм – приемлемо.

Проверку производим по формуле:

Вывод: принимаем выбранные квалитеты и допуски.

6.2.2. Вероятностный метод.

Повторяем начальные расчеты пункта 6.2.1.

Согласно [1],

,

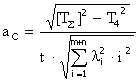где t – коэффициент, зависит от принятого процента риска Р и принимается по табл. 3.8. [1];

l – коэффициент относительного рассеяния; принимаем l=1/3, предполагая, что отклонения распределены по нормальному закону.

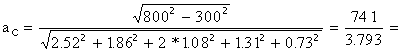195 – соответствует IT12.

Допуски, мм:

ТВ1=0.4, ТВ2=0.3, ТВ3=0.18, ТВ4=0.3, ТВ5=0.18, ТВ6=0.21, ТВ7=0.12.

 Проверка:

,

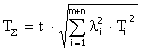мм – требуется понизить точность некоторых звеньев. Изготовим В2 и В6 по IT13.

Допуски, мм:

ТВ2=0.46, ТВ6=0.33.

.

Назначаем допуски на звенья, мм:

В1=157c12=;

В2=56js13=;

В3=12d12=;

В4=;

В5=13js12=;

В6=25js13=;

В7=5c12=.

Учитывая, что поле допуска js имеет =0, рассчитаем среднее отклонение поля допуска :

 ,

 – приемлемо. Проверка согласно формуле:

Вычислим t.

,

.

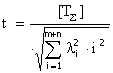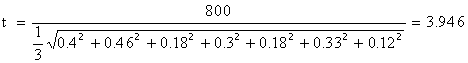t=3.946 – по табл. 3.8. процент риска Р=0.01 %.

Среднее отклонение считается аналогично пункту 6.2.1.

Вывод : вероятностный метод позволяет получить более грубые и более дешевые квалитеты при малой вероятности брака по сравнению с методом полной взаимозаменяемости. Следует предпочитать проведение расчетов вероятностным методом как более эффективным и экономически выгодным.

ЛИТЕРАТУРА

1. Палей М. А. Допуски и посадки: Справочник: В 2–х ч. –

Л.: Политехника, 1991.

2. Перель Л. Я., Филатов А. А. Подшипники качения: Расчет, проектирование и обслуживание опор: Справочник – М.:Машиностроение,1992.

3. Медовой М. А. Исполнительные размеры калибров: Справочник. В 2–х ч.– М.:Машиностроение,1980.