Индуктивная модель объяснения

8.2 Индуктивная модель объяснения

В последние десятилетия в логике и методологии все более широкое применение получает другая модель или схема научного объяснения, которая, правда, не обладает той убедительной силой и достоверностью, какая присуща дедуктивной модели. На этом основании ее иногда считают лишь временной попыткой объяснения, своего рода суррогатом, к которому приходится прибегать лишь в силу невозможности достижения более полного объяснения. Такой подход во многом определяется самим отношением к индукции, которая лежит в основе указанной модели объяснения. В самом деле, в то время как заключение дедуктивного вывода с логической необходимостью вытекает из посылок, заключение индукции, как правило, лишь в той или иной степени подтверждается этими посылками. Иными словами, если заключение дедукции имеет достоверный характер, то индукция обеспечивает лишь вероятные заключения. Вот почему сами индуктивные рассуждения иногда рассматривают лишь как эвристический способ мышления.

Необходимость обращения к индукции большей частью диктуется тем, что во многих объяснениях эмпирических наук приходится иметь дело со статистическими законами, выраженными в форме вероятностных утверждений. Как уже отмечалось, статистические законы в отличие от динамических характеризуют не индивидуальные события и явления, а только группы или классы однородных событий массового характера. Проще говоря, то, что утверждается в универсальном законе динамического типа, может быть перенесено на любой индивидуальный объект или событие. Статистические законы по своей природе не допускают такой возможности. Тем не менее, и такого рода законы можно использовать для объяснения и предсказания отдельных явлений и событий. В этих целях как раз и вводится теоретическое понятие вероятности, которое характеризует меру возможности осуществления события. Полнота объяснения и надежность предсказания в этом случае будут ниже, чем тогда, когда применяются универсальные законы динамического типа. Однако во многих важных ситуациях мы не располагаем подобными законами и поэтому должны обратиться к индуктивной схеме объяснения. Логический процесс, который мы используем для такого объяснения, очень часто определяют как индуктивную, или логическую вероятность. Он характеризует определенный тип связи между посылками и заключением объяснения, т.е. экспланансом и экспланандумом. Эта вероятность по своему значению существенно отличается от вероятности статистической, с которой мы встречаемся при формулировке законов массовых случайных явлений в физике, биологии и социологии. Во избежание недоразумений следовало, быть может, просто называть логическую вероятность индукцией, но с этим термином также связаны нежелательные ассоциации. Дело в том, что в традиционной логике под индукцией обычно понимается процесс рассуждения, идущий от частного к общему. В современной же индуктивной логике этим термином обозначается всякое рассуждение или умозаключение, посылки которого в той или иной степени подтверждают заключение, т.е. по сути дела вероятностное высказывание. Важно также отметить, что формальная структура индуктивной вероятности хорошо описывается известными еще со времен Бернулли и Лапласа аксиомами исчисления вероятностей. Вот почему нам кажется целесообразным сохранить термин “логическая, или индуктивная, вероятность” при описании схемы индуктивного объяснения или предсказания.

Общая схема индуктивно-статистического объяснения может быть представлена в следующем виде:

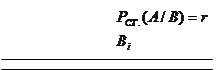
эксплананс (посылки делают

вероятным заключение)

экспланандум вероятно А

Большая посылка эксплананса такого объяснения представляет статистический закон, поэтому из него при фиксированных первоначальных условиях (меньшая посылка В_i) может быть выведено лишь индуктивное заключение об отдельном событии или явлении А. Это заключение имеет также вероятностный характер, но сама вероятность здесь существенно отличается от статистической, ибо она выражает непосредственно не информацию о реальных событиях, а характер логической связи между посылками и заключением индуктивного объяснения. Поскольку заключение или экспланандум объяснения здесь логически не вытекает из посылок, а лишь в той или иной степени подтверждается ими, то в самой схеме мы отделяем эксплананс от экспланандума двойной чертой и дополнительно указываем на вероятностный характер заключения. Если величина этой вероятности, или степень подтверждения, является известной, то она может быть точно указана в самой символической записи. В этом случае экспланандум индуктивно-статистического объяснения можно записать в следующем виде:

P_инд.(А/В_i)=k.

Это выражение представляет символическую запись индуктивного заключения А при наличии некоторой совокупности условий В_i. Таким образом, мы видим, что в индуктивно-статистическом объяснении используются две основные формы вероятности: статистическая и индуктивная (логическая). Если первая обеспечивает нас информацией о свойствах и закономерностях реального мира, то вторая устанавливает связь между экспланансом и экспланандумом объяснения.

При индуктивном объяснении с самого же начала возникает вопрос о том, какую степень подтверждения или логической вероятности следует признать достаточной для объяснения. Очевидно, если эта вероятность будет не больше половины, то такое объяснение вряд ли можно считать достаточно обоснованным. Равным образом мы не признаем надежным предсказание, вероятность которого не превосходит половины. Это обстоятельство существенно ограничивает класс индуктивных объяснений. Так, К. Гемпель относит к числу индуктивно-статистических объяснений только такие, степень вероятности которых приближается к 1. Иными словами, такого рода объяснения по существу приближаются к дедуктивным, так как их экспланандум вытекает из эксплананса почти с практической достоверностью (хотя теоретически практическая достоверность и отличается от достоверности дедуктивного заключения). В качестве конкретной иллюстрации Гемпель приводит пример с вытаскиванием шаров из урны, который достаточно ясно выражает его основную идею. Допустим, что мы наудачу вытаскиваем шар из урны, в которой находятся 999 белых и один черный шар. Если шары хорошо перемешаны, то вероятность извлечения белого Шара будет весьма велика (р = 0,999). Этот факт легко объяснить статистическими соображениями. Подобным же образом, по мнению Гемпеля, статистические законы, используемые при индуктивном объяснении, должны обладать такой высокой вероятностью, чтобы на их основе можно было делать надежные предсказания и объяснения. Некоторые авторы вообще отрицают правомерность индуктивного объяснения, утверждая, что в случае статистических обобщений и законов мы имеем дело не с объяснением, а с недостаточно надежными правилами недедуктивных умозаключений. Нетрудно заметить, что подобный подход к объяснению основывается на том, что единственно допустимой формой рассуждений в науке признается только дедукция, индуктивным же заключениям в лучшем случае отводится эвристическая роль. Вряд ли с таким подходом можно согласиться. Если индуктивно-статистические объяснения не признают за подлинные, полноценные объяснения, тогда следует также отказаться и от предсказаний, основанных на таких предпосылках. Но с этим не согласятся даже самые радикальные дедуктивисты.

И с теоретической и с практической точек зрения индуктивная модель объяснения играет существенную роль в науке. Часто она может значительно облегчить поиски более привычного дедуктивного объяснения, но во многих случаях сама проблема не допускает такого объяснения, и поэтому приходится обращаться к индукции и статистике.

В заключение остановимся на выяснении логической связи между дедуктивным и индуктивным объяснением. Поскольку индуктивный вывод допускает более ослабленные требования, чем дедуктивный, то целесообразно рассматривать индукцию как более общий тип рассуждения. Соответственно такому подходу мы будем выражать статистические законы в форме обобщенной, вероятностной импликации, впервые введенной Г. Рейхенбахом, а обычные универсальные законы динамического типа - в виде общей импликации математической логики.

В статистическом законе, как и любом вероятностном утверждении, можно выделить две части: в первой из них - антецеденте - формулируются условия, при осуществлении которых с той или иной вероятностью может произойти интересующее нас событие случайного массового характера, т.е. консеквент импликации. Так как при статистической интерпретации речь идет не об индивидуальных событиях, а о классе подобных событий, то в вероятностной импликации мы должны рассматривать не отдельные высказывания, а классы высказываний, которые можно выразить с помощью пропозициональных функций, или функций-высказываний. Тогда саму вероятностную импликацию символически можно представить в следующем виде:

Универсальный квантор (i) перед импликацией показывает, что она распространяется на все случаи из некоторого класса событий. Антецедент х_i, А обозначает класс тех событий А, при осуществлении которых с вероятностью равной р возникает событие у из класса В:

У_i В. Так, например, если рассматривать явления, связанные с радиоактивным распадом химических элементов (события класса А), то каждому элементу будет соответствовать определенная вероятность его превращения в другие элементы в течение некоторого времени, которую обычно характеризуют как период полураспада.

Существенное отличие вероятностной импликации от обычной состоит в том, что если в последнем случае истинность антецедента всегда влечет и истинность консеквента, то в первом случае истинный антецедент обеспечивает лишь определенную вероятность консеквента. Если степень вероятности р будет равна 1, тогда вероятностная импликация превращается в обычную. Мы видим отсюда, что дедуктивное объяснение можно рассматривать как особый случай индуктивного, когда степень вероятности экспланандума становится равной 1 и, следовательно, вероятный вывод становится достоверным.

Индуктивные объяснения, степень вероятности которых приближается к так называемой практической достоверности, т.е. весьма близка к 1, хотя по своему результату сходны с дедуктивными, тем не менее составляют особый вид, и поэтому Гемпель совершенно правильно относит их именно к индуктивным. Дело в том, что, несмотря на большую степень вероятности, их заключение в принципе может оказаться и неверным, так что здесь всегда имеется элемент неопределенности. Эта неопределенность будет возрастать по мере уменьшения величины вероятности. Поэтому индуктивные объяснения, степень вероятности заключения которых не превышает половины, на практике не будут считаться подлинными объяснениями.