Навигация
1.2 ПОЛУЧЕННЫЕ РЕЗУЛЬТАТЫ
По условию варианта определены следующие постоянные:
m = 15;
r = 10;
Определим характеристики посылаемых символов.
Вероятности символов Vi(они же - вероятности кода Zi), генерируемых источником рассчитываем по формуле 1.1.1. Полученные значения вероятностей приведены в таблице 1.2.2.
Сначала вероятности строятся по убыванию. После этого все вероятности делятся на две группы так, чтобы в пределах каждой группы их значения были примерно одинаковыми. В старший разряд кодов, соответствующих первой группе вероятностей, записывается 1,для второй группы кодов – 0. Затем каждая из полученных подгрупп, в свою очередь, делится аналогичным образом. При прохождении цикла деления по одному разряду происходит переход на разряд вправо. Деление продолжается до тех пор, пока в каждой группе не окажется по одному коду.
Результаты разработки кодов показаны в таблице 1.2.1.
Таблица 1.2.1 - Вероятности и коды символов
| Vi | P(Vi) | Zi | L(Zi) |
| 1 | 0.231 | 11 | 2 |
| 2 | 0.183 | 10 | 2 |
| 3 | 0.1408 | 011 | 3 |
| 4 | 0.1042 | 0101 | 4 |
| 5 | 0.0732 | 01001 | 5 |
| 6 | 0.0732 | 01000 | 5 |
| 7 | 0.0479 | 00111 | 5 |
| 8 | 0.0479 | 00110 | 5 |
| 9 | 0.0282 | 00101 | 5 |
| 10 | 0.0282 | 00100 | 5 |
| 11 | 0.0141 | 00011 | 5 |
| 12 | 0.0141 | 00010 | 5 |
| 13 | 0.0056 | 000011 | 6 |
| 14 | 0.0056 | 000010 | 6 |
| 15 | 0.0028 | 000000 | 6 |
Вычислим энтропию сообщения H(Z),бит/символ по формуле
1.1.2 :
H(Z) = 3.218 бит/символ
Среднюю длину неравномерного кода определим по формуле
1.1.3 :
Lср = 3.5652 бит
Максимальную энтропию неравномерного двоичного кода Zi определяем по формуле 1.1.4:
H(Z)max = 3.218 бит
По формуле 1.1.5 вычислим коэффициент эффективности Кэф неравномерного двоичного кода Zi:
Кэф = 0.903
Для расчета коэффициента избыточности Кизб воспользуемся формулой 1.1.6:
Кизб = 0.176
При простом кодировании повторением n=3 раз каждого двоичного сигнала сообщения Zi имеется два кода: Х1 и Х2, вероятности которых Р(Х1) и Р(Х2) находятся по формуле 1.1.7:
Р(Х1) = 0.4113 Р(Х2) = 0.5885
Вероятности возможных ошибок, при прохождении кода по каналу определяются по формулам 1.1.8 и 1.1.9 соответственно:
P10 = 0.3 P01 = 0.2
Канальная матрица P(Y/X) со стороны приемника для кода Х0 и Х1, рассчитанная по формуле 1.1.10, приведена в таблице 1.2.3. Для проверки расчета в последнем столбце таблицы 1.2.3 приведена сумма по текущей строке. Значения вероятностей в таблице 1.2.3 приводятся в десятитысячных долях единицы.
Таблица 1.2.2 - Канальная матрица P(Y/X)
| X | Y | сумма | |||||||
| 000 | 001 | 010 | 100 | 011 | 101 | 110 | 111 | ||
| 000 | 8000 | 0667 | 0667 | 0667 | 0000 | 0000 | 0000 | 0000 | 10000 |
| 111 | 0000 | 0000 | 0000 | 0000 | 1000 | 1000 | 1000 | 1000 | 10000 |
В таблице 1.2.3 приведены значения элементов канальной матрицы совместной вероятности P(X,Y), определенные по формуле 1.1.11. Значения вероятностей в таблице 1.2.3 приводятся в десятитысячных долях единицы.
Таблица 1.2.3 - Матрица совместных вероятностей P(X,Y)
| Х | Y | |||||||
| 000 | 001 | 010 | 100 | 011 | 101 | 110 | 111 | |
| 000 | 3292 | 0274 | 0274 | 0274 | 0000 | 0000 | 0000 | 0000 |
| 111 | 0000 | 0000 | 0000 | 0000 | 0588 | 0588 | 0588 | 4119 |
Элементы матрицы вероятностей P(Y) находятся по формуле 1.1.12. Полученные данные приведены в таблице 1.2.4 в десятитысячных долях единицы. В последнем столбце для проверки приведена сумма по строке.
Таблица 1.2.4 - Матрица P(Y)
| Y | Сумма | |||||||
| 000 | 001 | 010 | 100 | 011 | 101 | 110 | 111 | |
| 3292 | 0274 | 0274 | 0274 | 0588 | 0588 | 0588 | 4119 | 10000 |
Рассчитав матрицы P(X,Y) и P(Y), можно вычислить элементы матрицы условной вероятности P(X/Y) по формуле 1.1.13. Матрица P(X/Y) приведена в таблице 1.2.6.
Рассчитываем энтропию передаваемого сигнала H(X) и энтропию принимаемого сигнала H(Y) по формулам 1.1.14 и 1.1.15 соответственно:
H(X) = 0.9777 бит/символ
H(Y) = 2.2025 бит/символ
Условные энтропии H(X/Y) и H(Y/X) рассчитаем, воспользовавшись формулами 1.1.16 и 1.1.17 соответственно:
H(X/Y) = 0.0000 бит/символ
H(Y/X) = 1.2244 бит/символ
Таблица 1.2.5 - Матрица P(X/Y)
| X | Y | Сумма | |
| 000 | 111 | ||
| 000 | 1 | 0 | 1.0000 |
| 001 | 1 | 0 | 1.0000 |
| 010 | 1 | 0 | 1.0000 |
| 100 | 1 | 0 | 1.0000 |
| 011 | 0 | 1 | 1.0000 |
| 101 | 0 | 1 | 1.0000 |
| 110 | 0 | 1 | 1.0000 |
| 111 | 0 | 1 | 1.0000 |
По формуле 1.1.18 находим совместную энтропию H(X,Y):
H(X,Y) = 2.2014 бит/символ
Сделаем проверку полученных значений энтропий:
H(Y/X) + H(X) = 2.2025 бит/символ
H(X/Y) + H(Y) = 2.2025 бит/символ
Совпадение полученных значений свидетельствует о правильности найденных значений энтропий.
Определим значение взаимной энтропии I(X,Y), используя формулу 1.1.19:
I(X,Y) = 0.9777 бит/символ
Для отыскания следующих характеристик канала вычислим скорость передачи двоичных символов по каналу связи с помощью формулы 1.1.20:
V = 6000 символов/c
Информация передается по каналу связи с постоянной скоростью R, вычисляемой с помощью формулы 1.1.21:
R = 1956.1 бит/с
Производительность источника по формуле 1.1.22 равна:
![]() = 5868.3 бит/с
= 5868.3 бит/с
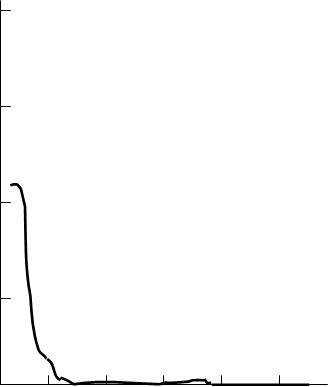
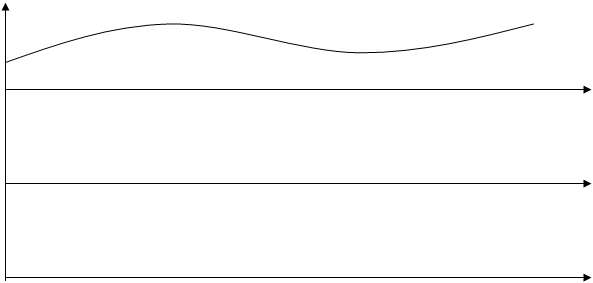
Результатом работы программы являются графики числа ошибок восстановления информации от параметра n (n,1) – кода и от p01 и p10. При теоретическом расчёте мы предположили, что в канале нет ошибок. Действительно, полученное нулевое значение энтропии H(X/Y) также об этом свидетельствует.
Однако полученный график говорит о том, что это предположение становится соответствующим действительности только начиная со значений n, равных 20..25.
Примерный вид полученных графиков приведен на рисунках 1.2.1 и 1.2.2.
45
Количество
ошибок,%
15
20 40 60 100
Количество повторений, n
Рисунок 1.2.1 – Число ошибок восстановления
![]()
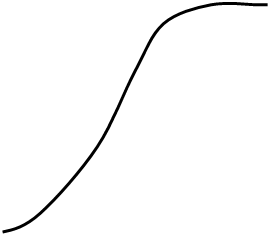
![]() 100
100
![]()
Количество
![]() ошибок,%
ошибок,%
![]() 15
15
![]()
20 40 60 100
p01,p10, %
Рисунок 1.2.1 – Число ошибок восстановления
1.3 ОПИСАНИЕ ПРОГРАММЫ
В соответствии с заданием мною была разработана программная модель канала с выводом графика зависимости числа ошибок от числа n. Программа написана на языке Borland Pascal 7.0.
Для программной реализации канала программа запрашивает длину передаваемого массива сообщений, число n и выполняет подсчет числа ошибок при его передаче. Затем идет расчет массива данных для построения графика зависимости числа ошибок от n для n, изменяющегося в интервале 1..100 с шагом 3. После этого происходит вывод на экран искомого графика.
В программе используются следующие процедуры и функции:
Функция flag может принимать булевское значение в зависимости от входной вероятности. Она служит для осуществления в программе случайного события с заранее заданной вероятностью.
Процедура ver рассчитывает ансамбль вероятностей исходного сообщения в зависимости от A и B, а также упорядочивает его по убыванию.
Процедура set_codes заполняет массив кодов по алгоритму Шеннона-Фэно и инициализирует маски для декодирования неравномерного кода.
Функция без параметров sourse при каждом обращении к ней принимает значение сообщения из ансамбля в соответствии с его вероятностью. Она использует тот же принцип, что и функция flag.
Процедура deranges вносит в код, соответствующий сообщению sourse, помехи в соответствии с моделью (n,1)-кода. В ней используются функции побитного сдвига shr и shl, а также функция flag.
Процедура decoder служит для раскодирования неравномерного двоичного кода после действия на него помех в канале. Поскольку наибольшая длина кода не превышает 8 бит, то для их хранения, передачи и декодирования используется тип данных – байт, причем располагаются они
в старших битах.
Процедура graphik служит для отображения на экране графика зависимости числа ошибок восстановления информации от значений параметра n (n,1) – кода. Всё изображение привязано к началу координат (x0,y0). Для удобства по
оси y откладываются значения в %. График отображается отрезками прямых для сглаживания резких скачков
значений.
1.4 ВЫВОД
В данном разделе были рассмотрены алгоритм построения неравномерного двоичного кода по алгоритму Шеннона-Фэно и такие характеристики кода и канала, как совместная энтропия, условная энтропия, производительность источника и т.д.
Кодирование информации по Шеннону-Фэно в сочетании с кодированием (n,1) кодом показало неплохие результаты при программном моделировании канала. Так, при передаче порядка 1000 символов при n = 20..25 практически не наблюдается ошибок при р10 и р01, определенных по заданию.
Похожие работы
... модуляцией, можно сделать вывод, что помехоустойчивость приемника, использующего в качестве информационного параметра фазу, почти приближена к вероятности ошибки приемника Котельникова. 3. Оптимальная фильтрация. Отметим, что оптимальный приемник, является корреляционным, сигнал на его выходе представляет собой функцию корреляции принимаемого и ожидаемого сигналов, благодаря чему ...
... : 2.4 Расчет энергетического потенциала Энергетическим потенциалом радиолинии называется отношение средней мощности сигнала к спектральной плотности шума, пересчитанное ко входу приемника. В задании курсового проектирования задана линия с расстоянием между приемником и передатчиком 200 км. Зададимся, что это линия Земля - управляемый объект. Линия связи подобного типа предназначена для ...
... работы необходимо начинать с приобретения методических руководств к курсовой работе Ниеталина Ж.Н. и Ниеталиной Ж.Ж. «Электрлiк байланыс теориясы» выпущенной в Алма-Ате в 1999 году, Ниеталина Ж.Н. и Ниеталиной Ж.Ж. «Теория электрической связи» учебное пособие к курсовой работе. Алма-Ата 2001г., а также учебное пособие Зюко А.Г. и др. «Теория передачи сигналов» – М.; «Связь» 1988г., «Теория ...
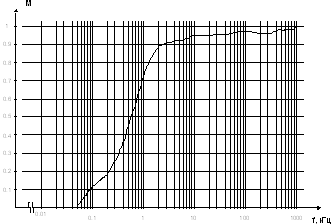
... имеет минимальное влияние. Таким диапазоном оказался диапазон от 200 кГц и выше, в котором устройство имеет характеристики удовлетворяющие условиям проведения измерений и организации передачи данных. Таким образом, для определения усредненной амплитудно-частотной характеристики сетей электропитания, провелся ряд экспериментальных измерений. Измерения проводились в условиях наиболее приближенным ...


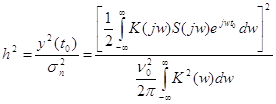




0 комментариев