Навигация
Уравнение апериодической границы устойчивости соответствует при Р=0
2. Уравнение апериодической границы устойчивости соответствует при Р=0.
Получаем:
![]() Þ К2 = 0
Þ К2 = 0
Найдем колебательную границу устойчивости, для этого подставим:
Р=jw
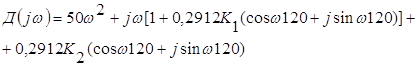
Тогда:
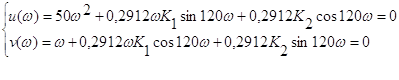
Решив уравнение относительно К1 и К2 , найдем выражение для колебательной границы устойчивости в виде:
![]()
![]()
Рассчитываем три точки колебательной границы устойчивости при w=0; Dw; 2Dw.
| w [c-1] | 0 | 0,005 | 0,01 |
| К1, | 3,434 | 3,3191 | 2,8446 |
| К2, | 0 | 0,0132 | 0,0382 |
СТУДЕНТ Ситников С.А. ГРУППА 2102
РАСЧЕТ ОБЛАСТИ УСТОЙЧИВОСТИ (ЛИНИИ РАВНОГО ЗАПАСА УСТ.) НЕПРЕР.АСР
ПАРАМЕТРЫ МОДЕЛЕЙ ИЗВЕСТНОЙ ЧАСТИ СИСТЕМЫ
МОДЕЛЬ ОБЪЕКТА ПО КАНАЛУ УПРАВЛЕНИЯ :
коэффициент передачи объекта = 112.0000
постоянная времени объекта = 50.0000
запаздывание объекта = 120.0000
Коэф.передачи исполн.устройства = 1.0000
Коэф.передачи регулир.органа = 0.0104
Коэффициент передачи датчика = 0.2500
РАСЧЕТ ОБЛАСТИ УСТОЙЧИВОСТИ
АПЕРИОДИЧЕСКАЯ ГРАНИЦА УСТОЙЧИВОСТИ K2 = 0
ТАБЛИЦА КОЛЕБАТЕЛЬНОЙ ГРАНИЦЫ УСТОЙЧИВОСТИ
W K1 K2
0.000000 -3.434066 0.000000
0.001538 -3.327219 0.001369
0.003077 -3.011959 0.005329
0.004615 -2.503887 0.011447
0.006154 -1.828233 0.019034
0.007692 -1.018726 0.027196
0.009231 -0.116080 0.034896
0.010769 0.833836 0.041032
0.012308 1.782074 0.044517
0.013846 2.678837 0.044370
0.015385 3.475768 0.039792
0.016923 4.128202 0.030245
0.018462 4.597282 0.015513
0.020000 4.851844 -0.004253
РАСЧЕТ ЛИНИИ РАВНОГО ЗАПАСА УСТОЙЧИВОСТИ
СТЕПЕНЬ КОЛЕБАТЕЛЬНОСТИ = 0.22
W K1 K2
0.000000 -3.434066 0.000000
0.001538 -2.954172 0.001362
0.003077 -2.334213 0.005027
0.004615 -1.620191 0.010232
0.006154 -0.858793 0.016105
0.007692 -0.095154 0.021747
0.009231 0.629134 0.026307
0.010769 1.277682 0.029049
0.012308 1.820598 0.029409
0.013846 2.235384 0.027029
0.015385 2.507436 0.021783
0.016923 2.630145 0.013783
0.018462 2.604631 0.003363
0.020000 2.439161 -0.008941
Область устойчивости системы в плоскости варьируемых параметров.
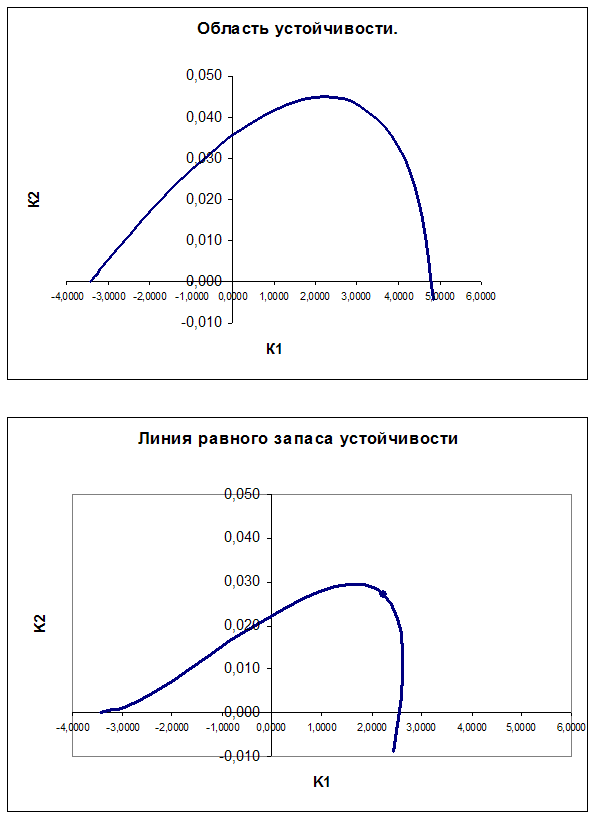
Определение направления штриховки колебательной границы устойчивости производится в соответствии со знаком определителя вида.
D(w)=![]()

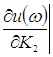 =
= 
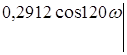 =
=

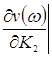

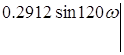
![]()
При перемещении вдоль колебательной границы в направлении возрастании частоты от 0 до ¥ кривая штрихуется слева, т. к. Dw > 0. Если частоту менять в пределах от - ¥ до 0 (w < 0), то определитель меняет знак и, двигаясь вдоль увеличения частоты, нужно штриховать правую часть кривой. Таким образом, кривая колебательной границы проходится дважды, при этом штрихуется одна и та же часть кривой двойной штриховкой. Апериодическая граница устойчивости штрихуется в сторону колебательной границы устойчивости.
Параметры регулятора K1 ; K2, выбранные из области устойчивости системы, обеспечат затухание переходной составляющей её движения при любых начальных отклонениях и внешних воздействиях.
Расчет линии равного запаса устойчивости.
1.Выведем выражение расширенной АФЧХ регулирующего блока Wр.б.(m1jw)
Передаточная функция:
 ,
,
Заменим р на (j - m)w:
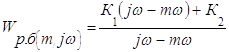
Запишем ![]() в виде
в виде
![]() =
=![]() , где
, где
![]() - расширенная АЧХ звена
- расширенная АЧХ звена
![]() -расширенная ФЧХ звена
-расширенная ФЧХ звена
Тогда:
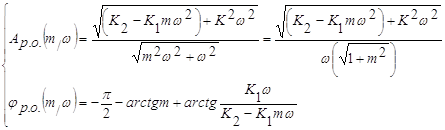
2.Выведем выражение расширенной АФЧХ части системы, содержащей остальные элементы в контуре управления.
![]()
![]() ,
,
![]() где
где ![]()
Заменим р на ![]()
![]()
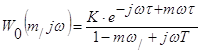
![]() , отсюда
, отсюда
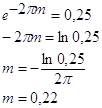
Запишем ![]() в виде
в виде
![]()
Тогда:
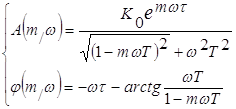
Между заданной степенью колебательности m системы и характером расширенных и частотных характеристик с тем же m существует определенная связь. Для нахождения системы на границе заданной степени колебательности m, определяющей заданный запас устойчивости, необходимо выполнение следующего соотношения:
![]()
или в показательной форме
![]()
или

Получили два условия.
Первое условие приводит к уравнению:

Второе условие к уравнению вида:
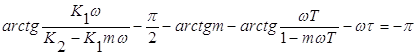
Решив уравнение относительно К1 и К2 получим:
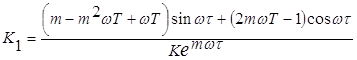

|
| 0 | 0,005 | 0,01 |
|
| 0 | 0,6 | 1,2 |
|
| 0 | 0,5646 | 0,932 |
|
| 1 | 0,8253 | 0,3642 |
|
| 1 | 1,1411 | 1,3021 |
|
| -0,0089 | -0,0059 | -0,0032 |
|
| 0 | 0 | 0,0001 |
Все значения К1 и К2, лежащие на кривой обеспечат заданные запас устойчивости. Значения К1 и К2, лежащие внутри области, ограниченной данной кривой и осями координат, обеспечат запас больше заданного или степень затухания больше заданной, а лежащие вне этой области – степень затухания меньше заданной. Специальными исследованиями было установлено, что настройки, расположенные чуть правее экстремума линии равного запаса устойчивости, обеспечивают минимум квадратичного интегрального критерия качества, поэтому эти настройки можно назвать оптимальными.
Получение переходного процесса системы на заданный вид воздействия.Рассмотрим операторный метод расчета непрерывных систем. Суть метода заключается в том, что каждый элемент непрерывной системы заменяется его дискретным аналогом, для этого вводим в модель непрерывного элемента импульсный элемент.
Дискретная модель системы.

Импульсную модель элемента можно описать разностным уравнением, вид которого определяется формирующим элементом. Самым простым формирующим элементом является экстраполятор нулевого порядка с передаточной функцией вида:
![]() , где Т0 – период дискретности. Тогда дискретная передаточная функция непрерывного элемента найдётся как:
, где Т0 – период дискретности. Тогда дискретная передаточная функция непрерывного элемента найдётся как: ![]()
Выбор периода дискретности Т0.
Допустимая погрешность моделирования определяется из условия выбора периода дискретности Т0 = Т/(10 ¸15), где Т – постоянная времени системы, при этом должно выполнятся условие: t / Т0 > 5 ¸ 10, где t - запаздывание системы.
![]()
Дискретная модель объекта регулирования:
 , где
, где ![]() ; m = t/T0 (число тактов запаздывания – целое число).
; m = t/T0 (число тактов запаздывания – целое число).
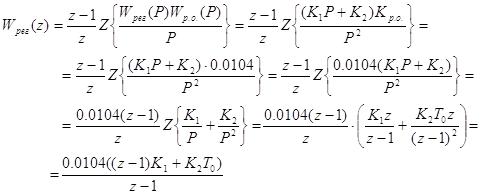
Дискретная модель датчика: Wдат (Z) = Kд = 0.25
Система разностных уравнений, описывающих работу данной АСР, при переходном процессе.
|
1. Уравнение регулируемого параметра:
![]()
![]()
yc[n] = 0.8yc[n - 1] + 22.4x[n - 13]
2. Уравнение датчика:
y1[n] = Кд×yc[n] = 0.25yc[n]
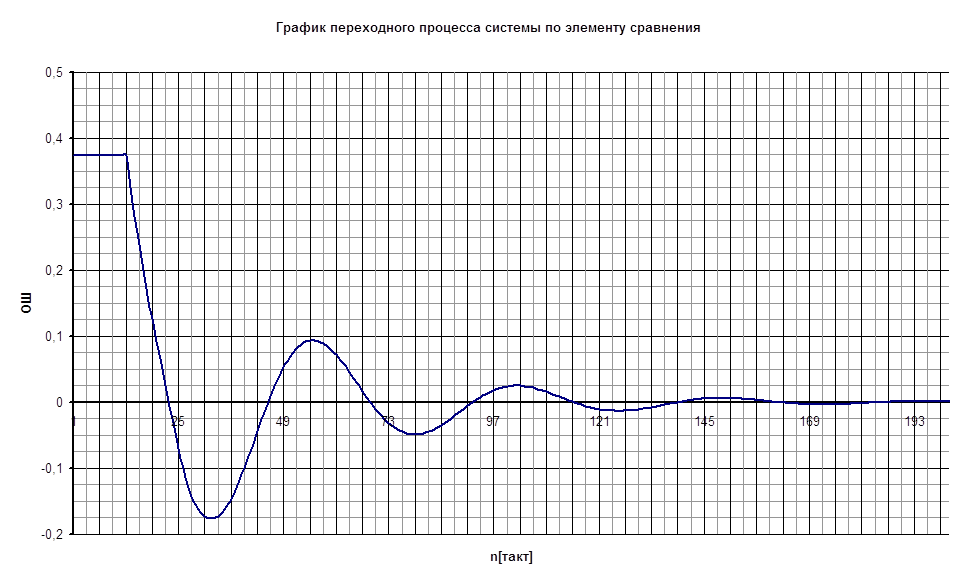
3. Уравнение элемента сравнения:
ОШ[n] = Dg ×Кд – y1[n] = 0.375 - y1[n]
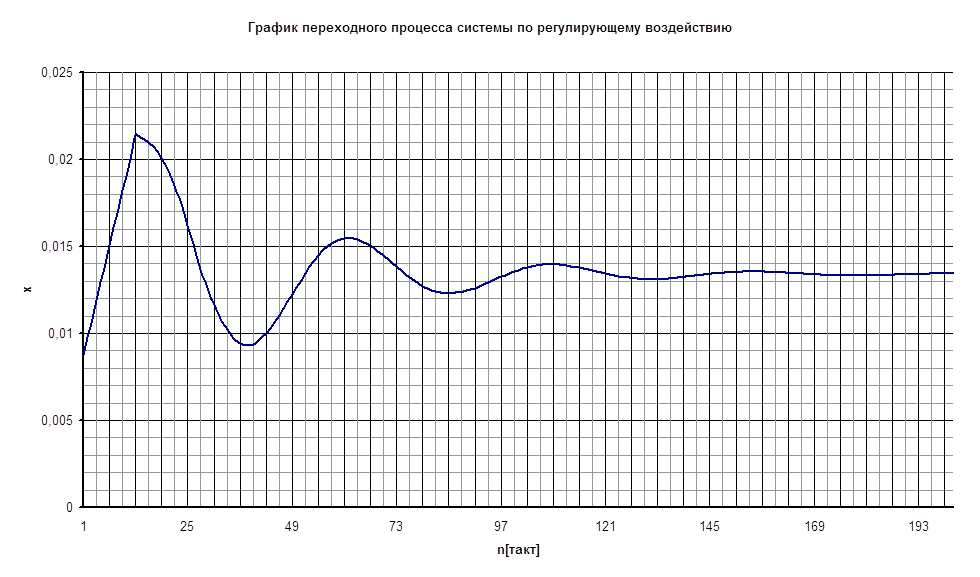
4. Уравнение регулирующего воздействия:
X[n] = X[n - 1] + Kр.о. ×K1× ОШ[n] + Kр.о. × (K2 T0 - K1 )× ОШ[n - 1]
X[n] = X[n - 1] + 0.0232 × ОШ[n] - 2.2316 × ОШ[n - 1]
Выбираем параметры настройки ПИ регулятора:
K1 = 2.234451
K2 = 0.027039
Отклонение регулируемой величины от установившегося значения должно быть не более 5%. D = 0.05 × | 1.5 | = 0.075
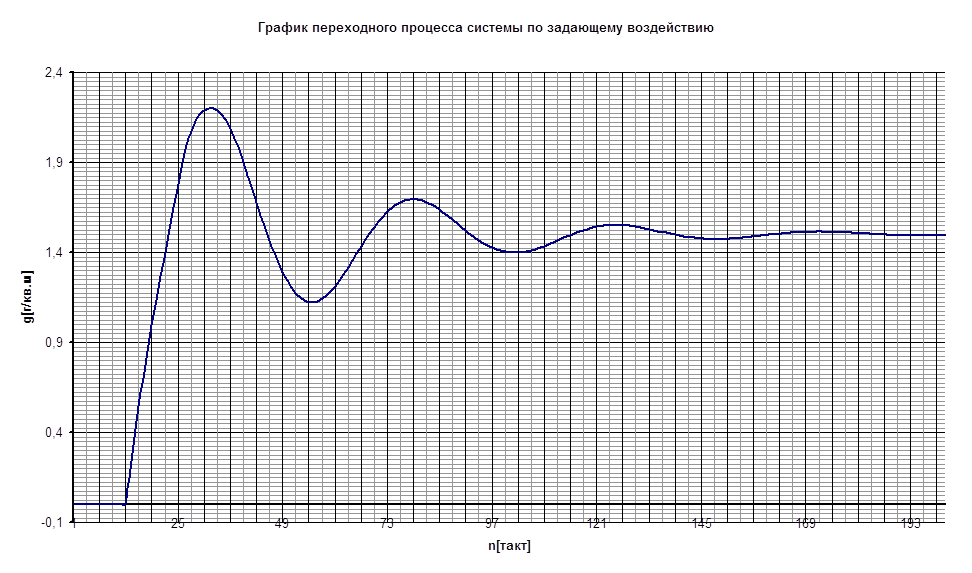
Расчёт переходного процесса системы по задающему воздействию
| n | t | Yc[n] | Y1[n] | ОШ[n] | X[n] |
| -13 | -130 | 0 | 0 | 0 | 0 |
| -12 | -120 | 0 | 0 | 0 | 0 |
| -11 | -110 | 0 | 0 | 0 | 0 |
| -10 | -100 | 0 | 0 | 0 | 0 |
| -9 | -90 | 0 | 0 | 0 | 0 |
| -8 | -80 | 0 | 0 | 0 | 0 |
| -7 | -70 | 0 | 0 | 0 | 0 |
| -6 | -60 | 0 | 0 | 0 | 0 |
| -5 | -50 | 0 | 0 | 0 | 0 |
| -4 | -40 | 0 | 0 | 0 | 0 |
| -3 | -30 | 0 | 0 | 0 | 0 |
| -2 | -20 | 0 | 0 | 0 | 0 |
| -1 | -10 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0,375 | 0,008714 |
| 1 | 10 | 0 | 0 | 0,375 | 0,009769 |
| 2 | 20 | 0 | 0 | 0,375 | 0,010823 |
| 3 | 30 | 0 | 0 | 0,375 | 0,011878 |
| 4 | 40 | 0 | 0 | 0,375 | 0,012932 |
| 5 | 50 | 0 | 0 | 0,375 | 0,013987 |
| 6 | 60 | 0 | 0 | 0,375 | 0,015042 |
| 7 | 70 | 0 | 0 | 0,375 | 0,016096 |
| 8 | 80 | 0 | 0 | 0,375 | 0,017151 |
| 9 | 90 | 0 | 0 | 0,375 | 0,018205 |
| 10 | 100 | 0 | 0 | 0,375 | 0,01926 |
| 11 | 110 | 0 | 0 | 0,375 | 0,020314 |
| 12 | 120 | 0 | 0 | 0,375 | 0,021369 |
| 13 | 130 | 0,195197 | 0,048799 | 0,326201 | 0,021289 |
| 14 | 140 | 0,374977 | 0,093744 | 0,281256 | 0,021162 |
| 15 | 150 | 0,542423 | 0,135606 | 0,239394 | 0,020981 |
| 16 | 160 | 0,700002 | 0,175001 | 0,199999 | 0,020738 |
| 17 | 170 | 0,849687 | 0,212422 | 0,162578 | 0,020431 |
| 18 | 180 | 0,993058 | 0,248264 | 0,126736 | 0,020055 |
| 19 | 190 | 1,131376 | 0,282844 | 0,092156 | 0,019608 |
| 20 | 200 | 1,265653 | 0,316413 | 0,058587 | 0,019087 |
| 21 | 210 | 1,396697 | 0,349174 | 0,025826 | 0,018491 |
| 22 | 220 | 1,525154 | 0,381289 | -0,00629 | 0,017817 |
| 23 | 230 | 1,651542 | 0,412885 | -0,03789 | 0,017065 |
| 24 | 240 | 1,776274 | 0,444069 | -0,06907 | 0,016234 |
| 25 | 250 | 1,899682 | 0,474921 | -0,09992 | 0,015323 |
| 26 | 260 | 1,99663 | 0,499157 | -0,12416 | 0,014479 |
| 27 | 270 | 2,071341 | 0,517835 | -0,14284 | 0,013696 |
| 28 | 280 | 2,127036 | 0,531759 | -0,15676 | 0,01297 |
| 29 | 290 | 2,166167 | 0,541542 | -0,16654 | 0,012302 |
| 30 | 300 | 2,190591 | 0,547648 | -0,17265 | 0,011692 |
| 31 | 310 | 2,201715 | 0,550429 | -0,17543 | 0,011142 |
| 32 | 320 | 2,200597 | 0,550149 | -0,17515 | 0,010655 |
| 33 | 330 | 2,188035 | 0,547009 | -0,17201 | 0,010235 |
| 34 | 340 | 2,164623 | 0,541156 | -0,16616 | 0,009888 |
| 35 | 350 | 2,130803 | 0,532701 | -0,1577 | 0,009617 |
| 36 | 360 | 2,086905 | 0,521726 | -0,14673 | 0,009428 |
| 37 | 370 | 2,033167 | 0,508292 | -0,13329 | 0,009328 |
| 38 | 380 | 1,969768 | 0,492442 | -0,11744 | 0,009321 |
| 39 | 390 | 1,900138 | 0,475034 | -0,10003 | 0,009396 |
| 40 | 400 | 1,826891 | 0,456723 | -0,08172 | 0,00954 |
| 41 | 410 | 1,752048 | 0,438012 | -0,06301 | 0,009745 |
| 42 | 420 | 1,677207 | 0,419302 | -0,0443 | 0,010003 |
| 43 | 430 | 1,603665 | 0,400916 | -0,02592 | 0,010305 |
| 44 | 440 | 1,532508 | 0,383127 | -0,00813 | 0,010646 |
| 45 | 450 | 1,464677 | 0,366169 | 0,008831 | 0,011017 |
| 46 | 460 | 1,401014 | 0,350254 | 0,024746 | 0,011412 |
| 47 | 470 | 1,342296 | 0,335574 | 0,039426 | 0,011822 |
| 48 | 480 | 1,289255 | 0,322314 | 0,052686 | 0,012241 |
| 49 | 490 | 1,242601 | 0,31065 | 0,06435 | 0,01266 |
| 50 | 500 | 1,203028 | 0,300757 | 0,074243 | 0,013071 |
| 51 | 510 | 1,171224 | 0,292806 | 0,082194 | 0,013465 |
| 52 | 520 | 1,147444 | 0,286861 | 0,088139 | 0,013834 |
| 53 | 530 | 1,13165 | 0,282912 | 0,092088 | 0,014174 |
| 54 | 540 | 1,123606 | 0,280901 | 0,094099 | 0,014479 |
| 55 | 550 | 1,122941 | 0,280735 | 0,094265 | 0,014748 |
| 56 | 560 | 1,129188 | 0,282297 | 0,092703 | 0,014977 |
| 57 | 570 | 1,141814 | 0,285453 | 0,089547 | 0,015164 |
| 58 | 580 | 1,160229 | 0,290057 | 0,084943 | 0,015309 |
| 59 | 590 | 1,183802 | 0,29595 | 0,07905 | 0,015411 |
| 60 | 600 | 1,21186 | 0,302965 | 0,072035 | 0,01547 |
| 61 | 610 | 1,243692 | 0,310923 | 0,064077 | 0,015488 |
| 62 | 620 | 1,278548 | 0,319637 | 0,055363 | 0,015466 |
| 63 | 630 | 1,315636 | 0,328909 | 0,046091 | 0,015406 |
| 64 | 640 | 1,354122 | 0,338531 | 0,036469 | 0,015312 |
| 65 | 650 | 1,393183 | 0,348296 | 0,026704 | 0,015187 |
| 66 | 660 | 1,432039 | 0,35801 | 0,01699 | 0,015037 |
| 67 | 670 | 1,469971 | 0,367493 | 0,007507 | 0,014864 |
| 68 | 680 | 1,506331 | 0,376583 | -0,00158 | 0,014674 |
| 69 | 690 | 1,540544 | 0,385136 | -0,01014 | 0,014471 |
| 70 | 700 | 1,572111 | 0,393028 | -0,01803 | 0,014259 |
| 71 | 710 | 1,600609 | 0,400152 | -0,02515 | 0,014043 |
| 72 | 720 | 1,625691 | 0,406423 | -0,03142 | 0,013826 |
| 73 | 730 | 1,647084 | 0,411771 | -0,03677 | 0,013614 |
| 74 | 740 | 1,664594 | 0,416149 | -0,04115 | 0,013408 |
| 75 | 750 | 1,678103 | 0,419526 | -0,04453 | 0,013214 |
| 76 | 760 | 1,687571 | 0,421893 | -0,04689 | 0,013034 |
| 77 | 770 | 1,69304 | 0,42326 | -0,04826 | 0,01287 |
| 78 | 780 | 1,69463 | 0,423658 | -0,04866 | 0,012725 |
| 79 | 790 | 1,692528 | 0,423132 | -0,04813 | 0,012601 |
| 80 | 800 | 1,68698 | 0,421745 | -0,04675 | 0,012498 |
| 81 | 810 | 1,678283 | 0,419571 | -0,04457 | 0,012417 |
| 82 | 820 | 1,666774 | 0,416693 | -0,04169 | 0,012358 |
| 83 | 830 | 1,65282 | 0,413205 | -0,0382 | 0,012322 |
| 84 | 840 | 1,636813 | 0,409203 | -0,0342 | 0,012308 |
| 85 | 850 | 1,619159 | 0,40479 | -0,02979 | 0,012314 |
| 86 | 860 | 1,600272 | 0,400068 | -0,02507 | 0,01234 |
| 87 | 870 | 1,580568 | 0,395142 | -0,02014 | 0,012384 |
| 88 | 880 | 1,560455 | 0,390114 | -0,01511 | 0,012444 |
| 89 | 890 | 1,540327 | 0,385082 | -0,01008 | 0,012519 |
| 90 | 900 | 1,520559 | 0,38014 | -0,00514 | 0,012605 |
| 91 | 910 | 1,501498 | 0,375375 | -0,00037 | 0,012701 |
| 92 | 920 | 1,483458 | 0,370865 | 0,004135 | 0,012805 |
| 93 | 930 | 1,466716 | 0,366679 | 0,008321 | 0,012914 |
| 94 | 940 | 1,451509 | 0,362877 | 0,012123 | 0,013026 |
| 95 | 950 | 1,438034 | 0,359509 | 0,015491 | 0,013138 |
| 96 | 960 | 1,426443 | 0,356611 | 0,018389 | 0,013249 |
| 97 | 970 | 1,416847 | 0,354212 | 0,020788 | 0,013357 |
| 98 | 980 | 1,409313 | 0,352328 | 0,022672 | 0,013459 |
| 99 | 990 | 1,403867 | 0,350967 | 0,024033 | 0,013554 |
| 100 | 1000 | 1,400495 | 0,350124 | 0,024876 | 0,013641 |
| 101 | 1010 | 1,399146 | 0,349787 | 0,025213 | 0,013719 |
| 102 | 1020 | 1,399735 | 0,349934 | 0,025066 | 0,013787 |
| 103 | 1030 | 1,402142 | 0,350536 | 0,024464 | 0,013843 |
| 104 | 1040 | 1,406225 | 0,351556 | 0,023444 | 0,013888 |
| 105 | 1050 | 1,411816 | 0,352954 | 0,022046 | 0,013922 |
| 106 | 1060 | 1,418727 | 0,354682 | 0,020318 | 0,013943 |
| 107 | 1070 | 1,426759 | 0,35669 | 0,01831 | 0,013954 |
| 108 | 1080 | 1,435702 | 0,358926 | 0,016074 | 0,013953 |
| 109 | 1090 | 1,445341 | 0,361335 | 0,013665 | 0,013943 |
| 110 | 1100 | 1,455459 | 0,363865 | 0,011135 | 0,013922 |
| 111 | 1110 | 1,465843 | 0,366461 | 0,008539 | 0,013893 |
| 112 | 1120 | 1,476287 | 0,369072 | 0,005928 | 0,013857 |
| 113 | 1130 | 1,486595 | 0,371649 | 0,003351 | 0,013813 |
| 114 | 1140 | 1,496584 | 0,374146 | 0,000854 | 0,013765 |
| 115 | 1150 | 1,506087 | 0,376522 | -0,00152 | 0,013712 |
| 116 | 1160 | 1,514955 | 0,378739 | -0,00374 | 0,013656 |
| 117 | 1170 | 1,523059 | 0,380765 | -0,00576 | 0,013599 |
| 118 | 1180 | 1,530292 | 0,382573 | -0,00757 | 0,01354 |
| 119 | 1190 | 1,536567 | 0,384142 | -0,00914 | 0,013483 |
| 120 | 1200 | 1,541822 | 0,385456 | -0,01046 | 0,013426 |
| 121 | 1210 | 1,546016 | 0,386504 | -0,0115 | 0,013373 |
| 122 | 1220 | 1,549129 | 0,387282 | -0,01228 | 0,013322 |
| 123 | 1230 | 1,551164 | 0,387791 | -0,01279 | 0,013276 |
| 124 | 1240 | 1,552142 | 0,388035 | -0,01304 | 0,013234 |
| 125 | 1250 | 1,552103 | 0,388026 | -0,01303 | 0,013198 |
| 126 | 1260 | 1,551104 | 0,387776 | -0,01278 | 0,013167 |
| 127 | 1270 | 1,549216 | 0,387304 | -0,0123 | 0,013142 |
| 128 | 1280 | 1,546522 | 0,386631 | -0,01163 | 0,013123 |
| 129 | 1290 | 1,543118 | 0,385779 | -0,01078 | 0,01311 |
| 130 | 1300 | 1,539104 | 0,384776 | -0,00978 | 0,013103 |
| 131 | 1310 | 1,534589 | 0,383647 | -0,00865 | 0,013102 |
| 132 | 1320 | 1,529683 | 0,382421 | -0,00742 | 0,013106 |
| 133 | 1330 | 1,524499 | 0,381125 | -0,00612 | 0,013115 |
| 134 | 1340 | 1,519147 | 0,379787 | -0,00479 | 0,013129 |
| 135 | 1350 | 1,513735 | 0,378434 | -0,00343 | 0,013147 |
| 136 | 1360 | 1,508368 | 0,377092 | -0,00209 | 0,013169 |
| 137 | 1370 | 1,503141 | 0,375785 | -0,00079 | 0,013193 |
| 138 | 1380 | 1,498143 | 0,374536 | 0,000464 | 0,01322 |
| 139 | 1390 | 1,493454 | 0,373364 | 0,001636 | 0,013249 |
| 140 | 1400 | 1,489144 | 0,372286 | 0,002714 | 0,013278 |
| 141 | 1410 | 1,485272 | 0,371318 | 0,003682 | 0,013308 |
| 142 | 1420 | 1,481884 | 0,370471 | 0,004529 | 0,013338 |
| 143 | 1430 | 1,479017 | 0,369754 | 0,005246 | 0,013368 |
| 144 | 1440 | 1,476696 | 0,369174 | 0,005826 | 0,013396 |
| 145 | 1450 | 1,474932 | 0,368733 | 0,006267 | 0,013423 |
| 146 | 1460 | 1,473728 | 0,368432 | 0,006568 | 0,013447 |
| 147 | 1470 | 1,473076 | 0,368269 | 0,006731 | 0,013469 |
| 148 | 1480 | 1,472957 | 0,368239 | 0,006761 | 0,013489 |
| 149 | 1490 | 1,473344 | 0,368336 | 0,006664 | 0,013506 |
| 150 | 1500 | 1,474201 | 0,36855 | 0,00645 | 0,01352 |
| 151 | 1510 | 1,475489 | 0,368872 | 0,006128 | 0,01353 |
| 152 | 1520 | 1,477158 | 0,369289 | 0,005711 | 0,013538 |
| 153 | 1530 | 1,479157 | 0,369789 | 0,005211 | 0,013542 |
| 154 | 1540 | 1,481431 | 0,370358 | 0,004642 | 0,013544 |
| 155 | 1550 | 1,483924 | 0,370981 | 0,004019 | 0,013542 |
| 156 | 1560 | 1,486576 | 0,371644 | 0,003356 | 0,013538 |
| 157 | 1570 | 1,48933 | 0,372332 | 0,002668 | 0,013532 |
| 158 | 1580 | 1,49213 | 0,373032 | 0,001968 | 0,013523 |
| 159 | 1590 | 1,494921 | 0,37373 | 0,00127 | 0,013512 |
| 160 | 1600 | 1,497653 | 0,374413 | 0,000587 | 0,0135 |
| 161 | 1610 | 1,500278 | 0,375069 | -6,9E-05 | 0,013486 |
| 162 | 1620 | 1,502753 | 0,375688 | -0,00069 | 0,013472 |
| 163 | 1630 | 1,505042 | 0,37626 | -0,00126 | 0,013456 |
| 164 | 1640 | 1,507111 | 0,376778 | -0,00178 | 0,013441 |
| 165 | 1650 | 1,508936 | 0,377234 | -0,00223 | 0,013425 |
| 166 | 1660 | 1,510495 | 0,377624 | -0,00262 | 0,01341 |
| 167 | 1670 | 1,511775 | 0,377944 | -0,00294 | 0,013395 |
| 168 | 1680 | 1,512766 | 0,378192 | -0,00319 | 0,013381 |
| 169 | 1690 | 1,513468 | 0,378367 | -0,00337 | 0,013368 |
| 170 | 1700 | 1,513882 | 0,37847 | -0,00347 | 0,013356 |
| 171 | 1710 | 1,514017 | 0,378504 | -0,0035 | 0,013346 |
СТУДЕНТ Ситников С.А. ГРУППА 2102
ИССЛЕДОВАНИЕ ЛИНЕЙНОЙ АСР ПРИ РАЗЛИЧНЫХ ВОЗДЕЙСТВИЯХ
МОДЕЛЬ ОБЪЕКТА ПО КАНАЛУ УПРАВЛЕНИЯ :
коэффициент передачи объекта = 112.0000
постоянная времени объекта = 50.0000
запаздывание объекта = 120.0000
Коэф.передачи исполн.устройства = 1.0000
Коэф.передачи регулир.органа = 0.0104
Коэффициент передачи датчика = 0.2500
ПЕРЕХОДНЫЙ ПРОЦЕСС ПО ЗАДАЮЩЕМУ ВОЗДЕЙСТВИЮ
Изменение задающего воздействия = 1.5000
ПИ - закон регулирования
Параметры закона регулирования :
Пропорциональная составляющая K1 = 2.2345
Интегральная составляющая K2 = 0.0270
Дискретность счета переходного процесса = 10.0000
ВРЕМЯ ЗАДАНИЕ РЕГ ОРГАН СИСТЕМА Ср.Квад.Ош.
160.0000000 1.5000000 0.0210865 0.6510940 0.1252132
170.0000000 1.5000000 0.0208436 0.7956272 0.1199796
180.0000000 1.5000000 0.0205269 0.9353699 0.1147136
190.0000000 1.5000000 0.0201348 1.0711906 0.1095526
200.0000000 1.5000000 0.0196659 1.2038003 0.1045969
210.0000000 1.5000000 0.0191190 1.3337810 0.0999210
220.0000000 1.5000000 0.0184932 1.4616092 0.0955806
230.0000000 1.5000000 0.0177878 1.5876752 0.0916181
240.0000000 1.5000000 0.0170022 1.7122984 0.0880660
250.0000000 1.5000000 0.0161358 1.8357403 0.0849498
260.0000000 1.5000000 0.0153094 1.9373479 0.0822463
270.0000000 1.5000000 0.0145229 2.0198114 0.0799121
280.0000000 1.5000000 0.0137772 2.0852575 0.0778947
290.0000000 1.5000000 0.0130747 2.1353655 0.0761392
300.0000000 1.5000000 0.0124183 2.1714592 0.0745921
310.0000000 1.5000000 0.0118120 2.1945815 0.0732034
320.0000000 1.5000000 0.0112599 2.2055516 0.0719279
330.0000000 1.5000000 0.0107670 2.2050126 0.0707261
340.0000000 1.5000000 0.0103385 2.1934679 0.0695641
350.0000000 1.5000000 0.0099797 2.1713114 0.0684141
360.0000000 1.5000000 0.0096963 2.1388500 0.0672545
370.0000000 1.5000000 0.0094943 2.0963225 0.0660695
380.0000000 1.5000000 0.0093795 2.0439143 0.0648495
390.0000000 1.5000000 0.0093439 1.9842299 0.0635947
400.0000000 1.5000000 0.0093801 1.9193960 0.0623117
410.0000000 1.5000000 0.0094816 1.8511763 0.0610116
420.0000000 1.5000000 0.0096421 1.7810594 0.0597076
430.0000000 1.5000000 0.0098554 1.7103270 0.0584134
440.0000000 1.5000000 0.0101155 1.6401055 0.0571426
450.0000000 1.5000000 0.0104161 1.5714055 0.0559073
460.0000000 1.5000000 0.0107508 1.5051522 0.0547178
470.0000000 1.5000000 0.0111129 1.4422078 0.0535822
480.0000000 1.5000000 0.0114952 1.3833890 0.0525060
490.0000000 1.5000000 0.0118904 1.3294795 0.0514923
500.0000000 1.5000000 0.0122905 1.2812400 0.0505413
510.0000000 1.5000000 0.0126873 1.2394150 0.0496509
520.0000000 1.5000000 0.0130736 1.2044481 0.0488171
530.0000000 1.5000000 0.0134435 1.1765553 0.0480342
540.0000000 1.5000000 0.0137915 1.1557790 0.0472955
550.0000000 1.5000000 0.0141134 1.1420267 0.0465939
560.0000000 1.5000000 0.0144053 1.1350983 0.0459225
570.0000000 1.5000000 0.0146642 1.1347064 0.0452745
580.0000000 1.5000000 0.0148874 1.1404887 0.0446441
590.0000000 1.5000000 0.0150731 1.1520182 0.0440261
600.0000000 1.5000000 0.0152202 1.1688082 0.0434168
610.0000000 1.5000000 0.0153281 1.1903172 0.0428132
620.0000000 1.5000000 0.0153969 1.2159499 0.0422137
630.0000000 1.5000000 0.0154275 1.2450597 0.0416176
640.0000000 1.5000000 0.0154214 1.2769482 0.0410251
650.0000000 1.5000000 0.0153810 1.3108999 0.0404374
660.0000000 1.5000000 0.0153088 1.3462052 0.0398559
670.0000000 1.5000000 0.0152080 1.3821778 0.0392826
680.0000000 1.5000000 0.0150817 1.4181646 0.0387193
690.0000000 1.5000000 0.0149337 1.4535546 0.0381681
700.0000000 1.5000000 0.0147675 1.4877838 0.0376307
710.0000000 1.5000000 0.0145869 1.5203400 0.0371084
720.0000000 1.5000000 0.0143958 1.5507661 0.0366022
730.0000000 1.5000000 0.0141981 1.5786632 0.0361128
740.0000000 1.5000000 0.0139974 1.6036936 0.0356403
750.0000000 1.5000000 0.0137973 1.6255834 0.0351843
760.0000000 1.5000000 0.0136013 1.6441261 0.0347442
770.0000000 1.5000000 0.0134125 1.6591849 0.0343191
780.0000000 1.5000000 0.0132337 1.6706932 0.0339077
790.0000000 1.5000000 0.0130675 1.6786501 0.0335088
800.0000000 1.5000000 0.0129159 1.6831170 0.0331210
810.0000000 1.5000000 0.0127808 1.6842113 0.0327430
820.0000000 1.5000000 0.0126636 1.6821010 0.0323734
830.0000000 1.5000000 0.0125652 1.6769990 0.0320113
840.0000000 1.5000000 0.0124864 1.6691563 0.0316558
850.0000000 1.5000000 0.0124273 1.6588563 0.0313060
860.0000000 1.5000000 0.0123879 1.6464083 0.0309616
870.0000000 1.5000000 0.0123679 1.6321418 0.0306222
880.0000000 1.5000000 0.0123664 1.6163996 0.0302876
890.0000000 1.5000000 0.0123826 1.5995315 0.0299579
900.0000000 1.5000000 0.0124151 1.5818878 0.0296333
910.0000000 1.5000000 0.0124626 1.5638131 0.0293140
920.0000000 1.5000000 0.0125233 1.5456400 0.0290002
930.0000000 1.5000000 0.0125955 1.5276845 0.0286922
940.0000000 1.5000000 0.0126774 1.5102410 0.0283902
950.0000000 1.5000000 0.0127670 1.4935793 0.0280945
960.0000000 1.5000000 0.0128624 1.4779404 0.0278052
970.0000000 1.5000000 0.0129615 1.4635353 0.0275223
980.0000000 1.5000000 0.0130627 1.4505419 0.0272459
990.0000000 1.5000000 0.0131639 1.4391047 0.0269757
1000.0000000 1.5000000 0.0132635 1.4293337 0.0267117
1010.0000000 1.5000000 0.0133598 1.4213046 0.0264537
1020.0000000 1.5000000 0.0134514 1.4150592 0.0262012
1030.0000000 1.5000000 0.0135370 1.4106063 0.0259541
1040.0000000 1.5000000 0.0136154 1.4079236 0.0257119
1050.0000000 1.5000000 0.0136857 1.4069599 0.0254745
ПЕРЕХОДНЫЙ ПРОЦЕСС ПО ВОЗМУЩЕНИЮ НА ВЫХОДЕ ОБЪЕКТА
Канал передачи возмущения - апериодическое звено 1 порядка
ПАРАМЕТРЫ КАНАЛА ПЕРЕДАЧИ ВОЗМУЩЕНИЯ
Коэффициент передачи канала возмущения = 1.1000
Постоянная времени канала возмущения = 60.0000
Возмущение ступенчатое
Значение возмущения = -3.0000
Дискретность счета переходного процесса = 10.0000
ВРЕМЯ ВОЗМ YF ОБЪЕКТ СИСТЕМА Ср.Квад.Ош.
0.000000 0.000000 0.000000 0.000000 0.000000
30.000000 -1.298449 0.000000 -1.298449 0.044026
60.000000 -2.085998 0.000000 -2.085998 0.118114
90.000000 -2.563671 0.000000 -2.563671 0.192940
120.000000 -2.853394 0.000000 -2.853394 0.258957
150.000000 -3.029119 0.166485 -2.862634 0.309076
180.000000 -3.135703 0.677008 -2.458695 0.327872
210.000000 -3.200349 1.349803 -1.850546 0.319704
240.000000 -3.239558 2.095556 -1.144002 0.295999
270.000000 -3.263340 2.864540 -0.398801 0.267365
300.000000 -3.277765 3.543583 0.265818 0.241694
330.000000 -3.286514 4.047102 0.760588 0.222506
360.000000 -3.291820 4.348739 1.056918 0.209291
390.000000 -3.295039 4.444880 1.149841 0.199622
420.000000 -3.296991 4.350097 1.053106 0.190957
450.000000 -3.298175 4.112383 0.814208 0.181841
480.000000 -3.298893 3.791970 0.493077 0.172135
510.000000 -3.299329 3.447541 0.148213 0.162485
540.000000 -3.299593 3.132691 -0.166902 0.153660
570.000000 -3.299753 2.889637 -0.410116 0.146089
600.000000 -3.299850 2.742393 -0.557457 0.139726
630.000000 -3.299909 2.697175 -0.602735 0.134214
660.000000 -3.299945 2.745037 -0.554908 0.129137
690.000000 -3.299967 2.864856 -0.435111 0.124222
720.000000 -3.299980 3.028208 -0.271771 0.119399
750.000000 -3.299988 3.204946 -0.095042 0.114750
780.000000 -3.299993 3.367705 0.067713 0.110398
810.000000 -3.299996 3.495293 0.195298 0.106417
840.000000 -3.299997 3.574872 0.274874 0.102802
870.000000 -3.299999 3.602518 0.302519 0.099485
900.000000 -3.299999 3.582358 0.282359 0.096382
930.000000 -3.299999 3.524734 0.224735 0.093427
960.000000 -3.300000 3.443767 0.143768 0.090596
990.000000 -3.300000 3.354732 0.054732 0.087893
1020.000000 -3.300000 3.271678 -0.028322 0.085333
1050.000000 -3.300000 3.205611 -0.094388 0.082929
1080.000000 -3.300000 3.163383 -0.136617 0.080673
1110.000000 -3.300000 3.147352 -0.152648 0.078549
1140.000000 -3.300000 3.155744 -0.144256 0.076536
1170.000000 -3.300000 3.183554 -0.116446 0.074616
Определение показателей качества системы регулирования.Оценку качества работы системы можно получить, анализируя кривую переходного процесса системы на заданный вид воздействия.
По задающему воздействию:
1. Точность системы управления в установившемся режиме работы.
Этот показатель оценивается величиной установившейся ошибки: ОШ¥ - точность, с которой поддерживается постоянство регулируемого параметра, определятся как разность между установившимся значением регулируемой величины после окончания переходного процесса y¥ и её заданным значением gзад, т.е. ОШ¥ = y¥ - gзад Из графика видно, что
y¥ = gзад = 1.5. это значит, что величина установившейся ошибки ОШ¥ = 0, т.е. полученная система не имеет систематической ошибки, сигнал на выходе системы, в установившемся режиме, равен сигналу задания.
2. Оценка быстродействия системы.
Быстродействие системы оценивается по времени переходного процесса, от момента начала воздействия до момента времени, после которого верно неравенство: | y(t) - y¥ | £ D, где D = (0.05 · y¥ ).
По графику переходного процесса найдём tп.пр. = 1070с » 18 мин.
Длительность переходного процесса велика.
3. Запас устойчивости (склонность системы к колебательности).
а). перерегулирование – максимальное отклонение регулируемой переменной от установившегося значения. ![]()
![]()
Величина d - велика, (допускается 10 ¸ 30 %).
б). затухание за период.
![]()
Затухание в допустимых пределах.
в). число колебаний за время переходного процесса – 2.
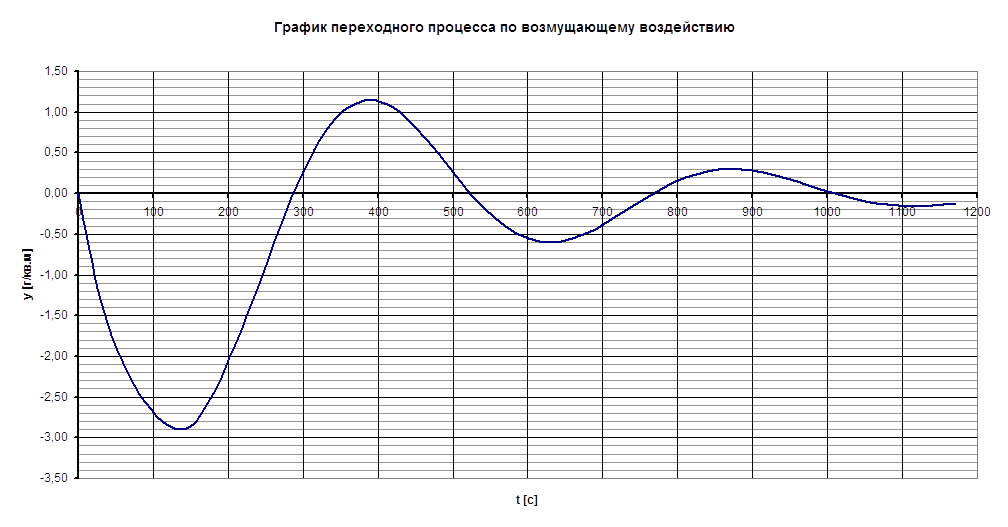
По возмущающему воздействию:
1. Оценка быстродействия системы.
Быстродействие системы оценивается по времени переходного процесса, от момента начала воздействия до момента времени, после которого верно неравенство: | y(t) - y¥ | £ D, где D = (0.05 · y¥ ).
По графику переходного процесса найдём tп.пр. = 700с » 11 мин.
2. Запас устойчивости (склонность системы к колебательности).
а). перерегулирование – максимальное отклонение регулируемой переменной от установившегося значения. ![]()
![]()
Величина d - хороший показатель, (допускается 10 ¸ 30 %).
б). затухание за период.
![]()
Затухание в допустимых пределах.
в). число колебаний за время переходного процесса – 1.
Анализ полученных результатов
Получили систему управления не обладающую статической ошибкой, имеющую хороший запас устойчивости, лежащий в пределах общетехнических нормативов.
За счёт снижения точности работы системы в установившемся режиме до допустимого значения можно несколько повысить запас устойчивости, выбрав другие настройки ПИ-регулятора.
Для выполнения более высоких требований к качеству переходного процесса можно ввести в систему дополнительно специальные корректирующие звенья с особо подобранной передаточной функцией, заменить регулятор с ПИ-законом регулирования на более сложный регулятор с ПИД-законом регулирования
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Похожие работы
... : группа 20+1 30+2 40+2 школьники 1400 р 1250 р 1150 р взрослые 1600р 1470р 1320р индивидуальные туристы 1980р Раздел 6. Состояние инфраструктуры г. Серпухов Город расположен в 99 км к Югу от Москвы. С Москвой Серпухов связан Варшавским и Симферопольским шоссе, а также железной дорогой Курского направления. Время в пути по железной дороге до станции метро " ...
... платы. 4.Расширение общественных фондов потребления снижало заинтересованность личности в результатах своего труда. 1 В Полном собрании сочинений В.И.Ленина нет никаких высказываний, о которых говорит И.В.Сталин. В.Н. Гузаров и Н.И. Гузарова Курс лекций «История России: 1861-1995 гг. Томск - 1999Глава 1. Введение к курсу «Истории России» Территория современной России, огромной страны, ...
... . Преимущество этого метода состоит в том, что они обеспечивают простую и короткую по количеству знаков идентификацию товара. Так шестизначный код товара в грузовой таможенной декларации 570310 согласно ТН ВЭД определяет продукцию как ковры и прочие текстильные напольные покрытия тафтинговые из овечьей шерсти или тонкой шерсти животных, а согласно Общероссийскому классификатору продукции ОК005-93 ...
... в Республике Беларусь для российских туристов» является туром выходного дня, основной целевой группой которого являются российские туристы. 3.2 Разработка нового туристского продукта экскурсионно-познавательной направленности «Памятные места Могилева в Республике Беларусь» Экскурсионно-познавательный тур «Памятные места Могилева в Республике Беларусь для российских туристов» отличается ...
0 комментариев