Напишите условие параллельности прямых на плоскости, заданных уравнениями с угловыми коэффициентами

121.           Напишите условие параллельности прямых на плоскости, заданных уравнениями с угловыми коэффициентами.

122.           Найдите уравнение плоскости, проходящей через три данные точки:
М₁ (3, 0, 0), М₂ (0, 1, 0), М₃ (0, 0, 1).

123.           Напишите каноническое уравнение гиперболического цилиндра. Какой координатной оси параллельна образующая этого цилиндра? Какая линия второго порядка является направляющей этого цилиндра?

124.           Найдите точки пересечения прямой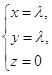  
 и сферы х² + у² + z² = 16.

125.           По характеристическим числам соответствующей квадратичной формы выяснить, какую невырожденную поверхность второго порядка определяет следующее уравнение: 5x² + 2y² + z² + 2xz = 5?

Зав. кафедрой

--------------------------------------------------

 

Экзаменационный билет по предмету

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

Билет № 27

126.           Напишите условие параллельности прямой и плоскости.

127.           Найдите уравнение плоскости, проходящей через три данные точки:
М₁ (3, 1, 0), М₂ (1, 2, 0), М₃ (0, 0, 0).

128.           Напишите каноническое уравнение двухполостного гиперболоида. Что называется полуосями этого гиперболоида?

129.           Какие плоскости симметрии имеет параболоид 2z =?

130.           Напишите характеристическое уравнение квадратичной формы:
х²-5у²-z²-10xz и найдите ее характеристические числа.

Зав. кафедрой

--------------------------------------------------

 

Экзаменационный билет по предмету

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

Билет № 28

131.           Что называется уравнением линии на плоскости Оху?

132.           Из точки (3, -2, 4) опустить перпендикуляр на плоскость
5х + 3у - 7z + 1= 0.

133.           Какие сечения называют коническими?

134.           Докажите, что прямая  лежит на гиперболоиде .

135.           Приведите к каноническому виду уравнение поверхности второго порядка
x² + y² + z² – 6yz = 4. Определить вид этой поверхности.

Зав. кафедрой

--------------------------------------------------

 

Экзаменационный билет по предмету

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

Билет № 29

136.           Какой вид имеет уравнение прямой, проходящей через две данные точки в пространстве.

137.           Найти координаты вектора, представляющего собой векторное произведение вектора  = (2, -1, 1) на вектор (1, 1, 0).

138.           Какая поверхность называется поверхностью вращения?

139.           Напишите каноническое уравнение гиперболического цилиндра с образующей, параллельной оси Оz.

140.           Приведите к каноническому виду уравнение поверхности второго порядка
8x² + 2y² + 5z² + 4yz = 48. Определить вид этой поверхности.

Зав. кафедрой

--------------------------------------------------

 

Экзаменационный билет по предмету

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

Билет № 30

141.           Напишите условие перпендикулярности прямых в пространстве.

142.           Найти координаты основания высоты, опущенной из вершины B треугольника ABC, если вершины известны: A(0, 5); B(1, 3); C(3, 0).

143.           Дайте определение конического сечения (коники).

144.           Меридиан  вращается вокруг оси Oz. Какая поверхность второго порядка получается?

145.           Приведите к каноническому виду уравнение поверхности второго порядка
x² + y² + 2z² – 8xy – 6xz + 24 = 0. Определить вид этой поверхности.

Зав. кафедрой

--------------------------------------------------

 

Экзаменационный билет по предмету

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

Билет № 31

146.           Какой вектор называется векторным произведением вектора  на вектор ?

147.           Докажите, что две прямые на плоскости перпендикулярны, если
 = (3, -1) и  = (2, 6) - их нормальные векторы.

148.           Напишите каноническое уравнение эллиптического цилиндра. Какой координатной оси параллельна образующая этого цилиндра? Какая линия второго порядка является направляющей этого цилиндра?

149.           Докажите, что прямая 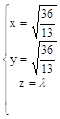, лежит на цилиндрической
поверхности .

150.           Напишите характеристическое уравнение квадратичной формы:
х²+4у²-2z²-2xz и найдите ее характеристические числа.

Зав. кафедрой

--------------------------------------------------

 

Экзаменационный билет по предмету

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

Билет № 32

151.           Известно, что  - направляющий вектор прямой в пространстве,  - нормальный вектор плоскости. Какой угол могут образовывать векторы  и , если прямая и плоскость перпендикулярны?

152.           Найти точку М₀ (x₀, y₀, z₀) пересечения плоскости 5x – 2y + z = 1 и
прямой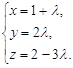

153.           Что называется текущими координатами на поверхности F(х, у, z) = 0?

154.           Докажите, что прямая  лежит на параболоиде .

155.           По характеристическим числам соответствующей квадратичной формы выяснить, какую невырожденную поверхность второго порядка определяет следующее уравнение: 4ху + 2х² + 5у² + 7z² = 70.

Зав. кафедрой

--------------------------------------------------

 

Экзаменационный билет по предмету

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

Билет № 33

156.           Что называется уравнением первой степени относительно х, у, z?

157.           Найти общее уравнение плоскости, проходящей через ось Оz и точку М(1, 1,0).

158.           Напишите каноническое уравнение эллипсоида.

159.           Найдите точку пересечения прямой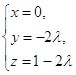
и гиперболоида х² + у² - z² = 1.

160.           С помощью какого преобразования координат приводится к каноническому виду уравнение поверхности второго порядка ? Как называется эта поверхность?

Зав. кафедрой

--------------------------------------------------

 

Экзаменационный билет по предмету

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

Билет № 34

161.           Напишите условие перпендикулярности двух плоскостей.

162.           Докажите, что две прямые на плоскости перпендикулярны, если
 = (3, 4) и  = (-8, 6) - их направляющие векторы.

163.           Дайте определение полуосей гиперболоида и эллипсоида.

164.           Меридиан у² - z² = 1 вращается вокруг оси Оz. Какая поверхность второго порядка при этом получается?

165.           Приведите к каноническому виду уравнение поверхности второго порядка
3x² + 3y² - z² + 2xy = 12. Определить вид этой поверхности.

Зав. кафедрой

--------------------------------------------------

 

Экзаменационный билет по предмету

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

Билет № 35

166.           Напишите условие перпендикулярности прямых на плоскости, заданных уравнениями с угловыми коэффициентами.

167.           Найти точку пересечения прямых 2х + 3у - 5 = 0 и х - у = 0, используя формулы Крамера.

168.                                                                                     Напишите уравнение второй степени относительно х, у, z.

169.           Как называется линия второго порядка, по которой плоскость  пересекает эллипсоид ? Напишите уравнение этого сечения.

170.           Напишите характеристическое уравнение для данной квадратичной формы и найдите ее характеристические числа: 12х² + 12z² - 4у² + 8ху.

Зав. кафедрой

--------------------------------------------------