Дайте определение понятия собственного числа линейного оператора А

119.            Дайте определение понятия собственного числа линейного оператора А.

120.            Определите, каким является базис а=(1/, 1/,1/), b=(1/, -1/, 0), с =(1/, 1/,-2/).

Зав. кафедрой

--------------------------------------------------

 

Экзаменационный билет по предмету

ЛИНЕЙНАЯ АЛГЕБРА

Билет № 26

121.            Приведение матрицы к ступенчатому виду методом Гаусса. Пример.

122.            Вычислить определитель матрицы det A, где А = 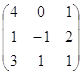 методом Гаусса.

123.            Образует ли линейное пространство множество функций, непрерывных на отрезке [a,b], относительно операций сложения функций и умножения функции на число?

124.            Какая квадратичная форма называется неотрицательно определенной?

125.            Найдите ранг квадратичной формы трех переменных х² + 2ху +z².

Зав. кафедрой

--------------------------------------------------

 

Экзаменационный билет по предмету

ЛИНЕЙНАЯ АЛГЕБРА

Билет № 27

126.            Какой вектор называют решением линейной системы уравнений? Что значит решить систему линейных уравнений? Какие системы называют эквивалентными?

127.            Найти матрицу А^-1, обратную к матрице А и с ее помощью решить систему А = , где А = , = , .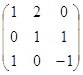

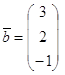128.            Дайте определение размерности линейного пространства.

129.            При каком условии существует базис, в котором матрица линейного оператора является диагональной?

130.            В ортонормированном базисе оператор А имеет матрицу А = 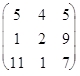. Найдите матрицу сопряженного ему оператора в этом же базисе.

Зав. кафедрой

--------------------------------------------------

 

Экзаменационный билет по предмету

ЛИНЕЙНАЯ АЛГЕБРА

Билет № 28

131.            Какую матрицу называют невырожденной? При каком значении определителя строки матрицы являются зависимыми, а при каком – независимыми?

132.            Найти ранг матрицы: A = .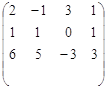

133.            Сформулируйте необходимое и достаточное условие линейной зависимости векторов.

134.            Какой вектор называется собственным вектором оператора?

135.            Составьте характеристическое уравнение для оператора А, если его матрица А=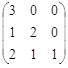. Найдите собственные значения оператора А.

Зав. кафедрой

--------------------------------------------------

 

Экзаменационный билет по предмету

ЛИНЕЙНАЯ АЛГЕБРА

Билет № 29

136.            Какую матрицу называют матрицей системы уравнений? Какая матрица называется расширенной матрицей системы? Как записываются вектор неизвестных и вектор правых частей уравнений?

137.            Сколько решений может иметь система уравнений: ?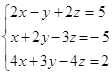

138.            Напишите зависимость, связывающую матрицы А_b и А_е в различных базисах b и e линейного пространства.

139.            Сколько собственных значений имеет самосопряженный оператор, действующий в n-мерном евклидовом пространстве?

140.            Не проводя вычислений, выясните, является ли система векторов а₁=(-4, 2, 3), а₂= (-3, 5, 1), а₃ = (1,-7, 3), а₄= (12,-5,4) линейно независимой.

Зав. кафедрой

--------------------------------------------------

 

Экзаменационный билет по предмету

ЛИНЕЙНАЯ АЛГЕБРА

Билет № 30

141.            Какую матрицу называют единичной, нулевой, треугольной? Пример.

142.            Сколько решений может иметь система уравнений: ?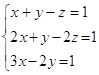

143.            Какой вид у матрицы тождественного оператора, действующего в пространстве L?

144.            Дайте определение оператора, сопряженного к данному линейному оператору А.

145.            Запишите матрицу перехода от базиса b к новому с, если b₁=с₁-3с₂+2с₃, b₂=-2с₁+с₂ - с₃, b₃=с₁+2с₂-2с₃.

Зав. кафедрой

--------------------------------------------------

 

Экзаменационный билет по предмету

ЛИНЕЙНАЯ АЛГЕБРА

Билет № 31

146.            Как записывается формула разложения определителя по строке или столбцу? Пример.

147.            Найти матрицу , обратную к матрице А и с ее помощью решить систему , где , , .

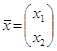148.            Запишите неравенство Коши - Буняковского.

149.            Дайте определение самосопряженного оператора.

150.            Приведите квадратичную форму х₁² + 4х₁х₂ + x₂x₃ + x₃² к каноническому виду методом выделения квадратов.

Зав. кафедрой

--------------------------------------------------

 

Экзаменационный билет по предмету

ЛИНЕЙНАЯ АЛГЕБРА

Билет № 32

151.            Неоднородная система линейных уравнений. Ее общее и частное решения. Пример.

152.            Найти ранг матрицы: A =.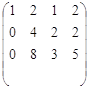

153.            Дайте понятие ортонормированного базиса линейного пространства.

154.            Как находятся собственные векторы линейного оператора?

155.            Пусть l₁, l₂,.., l_n - собственные значения оператора А. Найдите собственные значения линейного оператора, матрицей которого является матрица А².

Зав. кафедрой

--------------------------------------------------

 

Экзаменационный билет по предмету

ЛИНЕЙНАЯ АЛГЕБРА

Билет № 33

156.            Однородные системы уравнений и их основные свойства.

157.            Сколько решений может иметь система уравнений: ?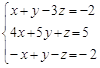

158.            Каким аксиомам подчиняется норма вектора?

159.            Какая квадратичная форма называется положительно определенной?

160.            Запишите матрицу перехода от базиса b к новому с, если b₁= 4с₁- с₂+9с₃, b₂ =-с₁+6с₂-11с₃, b₃=5с₁+3с₂-2с₃.

Зав. кафедрой

--------------------------------------------------

 

Экзаменационный билет по предмету

ЛИНЕЙНАЯ АЛГЕБРА

Билет № 34

161.            Понятие «определитель» применительно к матрице третьего порядка. Какую величину называют алгебраическим дополнением элемента? Пример.

162.            Даны матрицы  и . Найти АВ-ВА.

163.            Какое пространство называется евклидовым?

164.            Когда матрица оператора А подобна некоторой диагональной?

165.            Выясните, образуют ли векторы а₁=(1, 0, 0, 0), а₂= (1, 1, 0, 0), а₃ = (1,1, 1, 0), а₄= (1,1,1, 1) базис в линейном арифметическом пространстве R⁴.

Зав. кафедрой

--------------------------------------------------

 

Экзаменационный билет по предмету

ЛИНЕЙНАЯ АЛГЕБРА

Билет № 35

166.            Задача межотраслевого баланса. Ее математическая модель.

167.            Исследовать и решить в случае совместности систему уравнений: .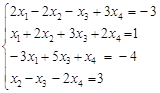

168.            Что означает запись dim V?

169.            Что такое квадратичная форма?

170.            Пусть l₁, l₂,.., l_n - собственные значения оператора А. Найдите собственные значения линейного оператора, матрицей которого является матрица А^-1.

Зав. кафедрой

--------------------------------------------------