Навигация
Информация, которую можно получить, изучая кривую блеска звезды типа Алголя
2.2. Информация, которую можно получить, изучая кривую блеска звезды типа Алголя
Математическая обработка кривой изменения блеска даёт возможность получить ценную информацию о двойной системе. Приведём простейший пример, предположив, что компоненты шарообразны и движутся вокруг общего центра масс системы по круговым орбитам. Обозначим массу первой компоненты через М1и через a1 радиус орбиты первой компоненты, через М2 и a2 - массу и радиус орбиты второй компоненты. Из определения центра масс следует соотношение:
![]() ,
(2.1)
,
(2.1)
так как центр масс расположен между компонентами на расстояниях от них, обратно пропорциональных их массам.
Обозначим радиус относительной орбиты, т.е. расстояние между центрами компонент через a:
![]() , (2.2)
, (2.2)
радиус первой компоненты через R1 , радиус второй компоненты через R2.
Тогда можно ввести следующие отношения:
![]() и
и ![]() , (2.3)
, (2.3)
которые являются двумя элементами системы, определяемые из анализа кривой блеска.
Если Е1 - блеск первой (определение блеска небесного светила см. выше), а Е2 - блеск второй компоненты, то суммарный блеск системы вне затмения:
![]() (2.4)
(2.4)
Разделим последнее равенство на Е и введём обозначения:
![]() и
и![]() (2.5)
(2.5)
Величины ![]() и
и ![]() являются третьим и четвёртым элементами системы. Они, очевидно, связаны соотношением:
являются третьим и четвёртым элементами системы. Они, очевидно, связаны соотношением:
![]() (2.6)
(2.6)
Существует и пятый элемент системы. Плоскость, перпендикулярная лучу зрения называется картинной плоскостью. Плоскость относительной орбиты двойной звезды пересекает картинную плоскость по прямой, называемой линией узлов. Наклон относительной орбиты к картинной плоскости называется наклонением орбиты и обозначается через i. Наклонение орбиты- есть пятый элемент системы. У затменно-переменных величина i близка к 90º, иначе бы не происходило затмений.
Из кривой блеска можно определить все 5 элементов. Особенно надёжно они вычисляются при полном затмении. Например, вычислим ![]() и
и ![]() . Допустим, что первая компонента с большим радиусом R1 закрывает вторую компоненту, имеющую радиус R2 .
. Допустим, что первая компонента с большим радиусом R1 закрывает вторую компоненту, имеющую радиус R2 .
Вне затмения мы воспринимаем полный блеск системы E; звёздная величина вне затмения – m0 . Во время полной фазы мы воспринимаем блеск только от большой звезды с блеском Е1, которая закрывает более яркую, но меньшую по размерам компоненту. Если звёздная величина во время полной фазы затмения m1 , то можно определить отношение блесков Е1 к E:
 (2.7)
(2.7)
Найдя по логарифму число, получим l1 , а затем найдём ![]()
Например, для уже упоминавшейся звезды U Цефея звёздная величина в максимуме
m0 =6,63, а во время полной фазы затмения m1=9,79. Поэтому в данном случае:
![]() ,
,
откуда ![]() и
и ![]()
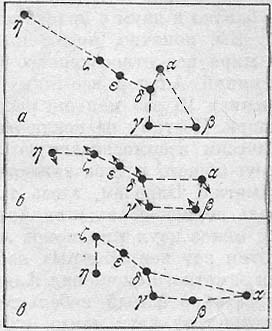
Значительно труднее определить r1и r2 , поскольку для этого нужно знать наклонение орбиты. Упростим задачу, положив (с некоторой погрешностью) i =90°, т.е. будем считать, что затмение полное и центральное. Рис.4 показывает обстоятельства затмения при двух положениях дисков компонент: вначале затмения (Рис.4, а) и вначале полной фазы (Рис.4 б).
В начале затмения диски компонент находятся во внешнем касании, поэтому видимое расстояние между их центрами равно ![]() , а угол в орбите равен q1 . В начале полной фазы затмения диски находятся во внутреннем касании и расстояние между их центрами равно
, а угол в орбите равен q1 . В начале полной фазы затмения диски находятся во внутреннем касании и расстояние между их центрами равно ![]() , а соответствующий угол в орбите равен q2.
, а соответствующий угол в орбите равен q2.
Из треугольников (см. рис.4) видно, что:
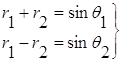 , (2.8)
, (2.8)
где a – радиус относительной орбиты.
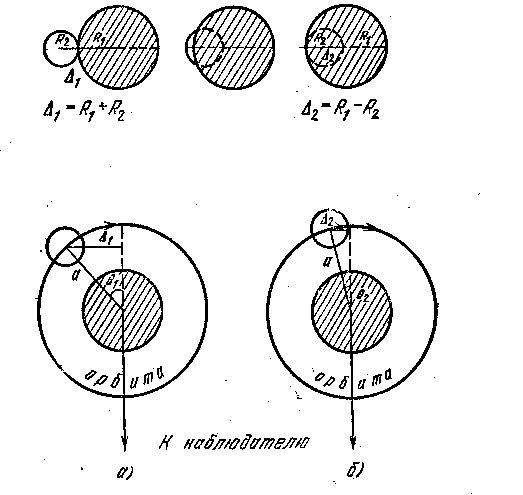
Рис.4
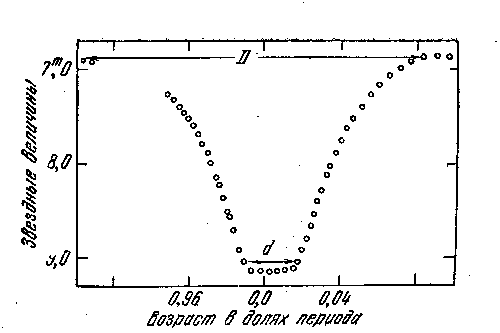
Рис.5
Чтобы решить эту систему уравнений относительно r1 и r2 , нужно знать углы q1 иq2 , их определяют из кривой блеска.
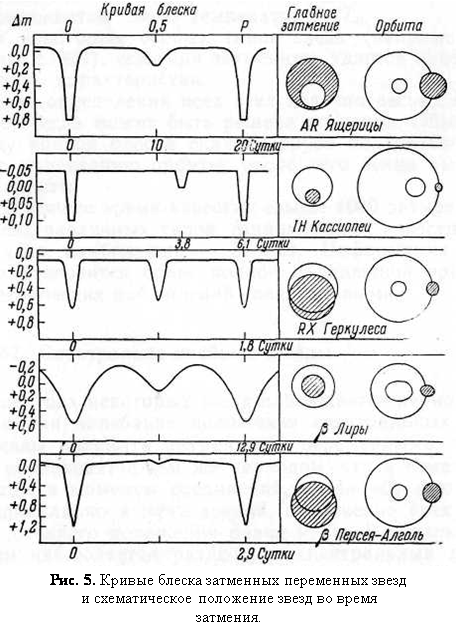
Если орбита круговая, то орбитальная скорость движения постоянна и угол q растёт пропорционально времени, увеличиваясь на 360° за один период P. По кривой блеска можно определить продолжительность затмения D и продолжительность полной фазы d в долях периода. (Рис.5). Нетрудно видеть, что углы q1 иq2 связаны с величинами D и d следующими соотношениям и:
![]()
(2.9)![]()
Решая уравнения (2.8), можно получить значения r1 и r2 .
Для звезды U Цефея, часть кривой блеска которой изображена на рис.5, период P=2,493 суток. Из кривой блеска следует, что D=0,160 и d=0,039, откуда q1=28,8° и q1=7,02°. Решая уравнения (2.8), получаем r1=0,302 и r2=0,180.
Таким образом, в системе U Цефея относительный радиус большей звезды r1=0,302, а на долю её излучения приходится всего l1=0,0545 общего излучения системы. Малая же звезда несмотря на меньший радиус обладает гораздо большей светимостью. Такое распределение излучения между компонентами вызвано различиями их температур[1].
К сожалению, из кривой блеска нельзя определить ни абсолютные размеры системы, ни массы компонент. Для этого необходимы ещё и спектральные наблюдения, позволяющие определить лучевые скорости звёзд.
Похожие работы
... водорода, в то время как у звезд с температурой около 6 тыс. К. линии ионизированного кальция, расположенные на границе видимой и ультрафиолетовой части спектра. Заметим, что такой вид I имеет спектр нашего Солнца. Последовательность спектров звёзд, получающихся при непрерывном изменении температуры их поверхностных слоёв, обозначается следующими буквами: O, B, A, F, G, K, M, от самых горячих к ...
... русских академиков. Круг его интересов и исследований в естествознании охватывал самые различные области фундаментальных и прикладных наук (физика, химия, география, геология, металлургия, астрономия). Ломоносов глубоко проник в материалистическую сущность природы, пропагандировал и развивал её основные физические и философские принципы: закон сохранения материи и движения, принципы познаваемости ...
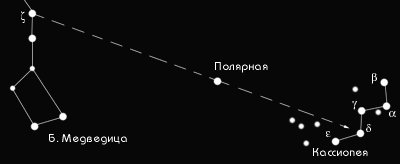
... здесь что-нибудь другое, более ему нравящееся, но во всяком случае тут на небе оказывается слишком большая пустота, чтобы оставлять ее ничем не заполненной”. После этого общего обзора околополярных созвездий познакомимся подробнее с каждым из них в отдельности. На современных звездных картах созвездие Большой Медведицы занимает гораздо большее место, чем то семизвездие в форме ковша, с ...
... линий наблюдаться не будет (из-за слабости спектра спутника), но линии спектра главной звезды колебаться будут так же, как и в первом случае. Периоды изменений, происходящих в спектрах спектрально-двойных звезд, очевидно, являющиеся и периодами их обращения, бывают весьма различны. Наиболее короткий из известных периодов 2,4Ч (g Малой Медведицы), а наиболее длинные – десятки лет. Для ...


0 комментариев