Навигация
VаR – модели оценки инвестиционных рисков
2.2. VаR – модели оценки инвестиционных рисков
Для всесторонней (количественной и качественной) оценки рыночного риска в настоящее время в мире все активнее используется методология Value-at-Risk (VaR). Существует множество неточных переводов и понятий "Value-at-Risk" типа "стоимость под риском", "стоимостная оценка (мера) риска" или даже "рисковая стоимость" и т.п., но, по мнению экспертов, подобные термины в научно-практической литературе следует использовать без перевода, используя латинские аббревиатуры и стараясь по возможности математически точно определять эти понятия с практическими иллюстрациями на примерах, применяя единую аббревиатуру. Тем не менее даже в англоязычной литературе для Value-at-Risk используются две аббревиатуры - VAR и VaR. Правильно применять последний вариант аббревиатуры, т.е. VaR, так как аббревиатура VAR может иногда употребляться в одной и той же зарубежной статьедля обозначения и Value-at-Risk и дисперсии (Variance). Латинская аббревиатура VaR применяется на практике и в теории исключительно для обозначения Value-at-Risk, поэтому везде в данной работе только она и будет использоваться.
VaR - это вероятностно-статистический подход для определения соотношения ценовых показателей и риска, основным понятием в нем является распределение вероятностей, связывающее все возможные величины изменений рыночных факторов с их вероятностями.
Методология VaR стала особенно широко применяться в последние годы и сегодня используется в качестве единого унифицированного подхода к оценке риска международными банковскими и финансовыми организациями. Например, Банк международных расчетов (BIS) применяет VaR в качестве основы при установлении нормативов величины собственного капитала относительно риска активов.
Кроме единства и относительной простоты подхода, главным и, видимо, самым веским аргументом в пользу концепции VaR является тот факт, что VaR стала общепризнанной методологией оценки риска среди зарубежных организаций и финансистов.
Сторонники данной концепции верят, что в конечном итоге VaR позволит на общем языке обсуждать проблемы оценки риска финансовым директорам, бухгалтерам, акционерам, управленцам, аудиторам и регулирующим органам всех стран. Методология VaR обладает рядом других несомненных преимуществ, так как позволяет:
- оценить риск в терминах возможных потерь, соотнесенных с вероятностями их возникновения;
- измерить риски на различных рынках универсальным образом;
- агрегировать риски отдельных позиций в единую величину для всего портфеля, учитывая при этом информацию о количестве позиций, волатильности на рынке и периоде поддержания позиций.
К другим важным достоинствам VaR относятся: простота и наглядность расчётов, консолидация информации, возможность сравнительного анализа потерь и соответствующих им рисков, а также то, что сам процесс оценки риска не менее важен, чем результат. VaR -своеобразный способ мышления и рассуждения о рисках.
К недостаткам VaR относятся сильные и слабые допущения о свойствах финансовых рынков, поведении экономических агентов на этих рынках, о виде и параметрах эмпирической функции распределения вероятностей, о чувствительности портфеля и ряд других.
При оценке VaR практически не учитывается ликвидность - важная характеристика всех рынков, особенно российских. Это может привести к тому, что в отдельные моменты изменение структуры портфеля для уменьшения риска может оказаться бесполезным.
Методология VaR применима на стабильных рынках и перестает адекватно отображать величину риска, когда на рынках происходят быстрые и/или резкие изменения. Если рыночные условия существенно меняются, например, скачкообразно изменяются цены, резко изменяется ликвидность рынка или корреляция между активами, то VaR учтет эти изменения через определенный промежуток времени, только накопив необходимую статистику событий и данных. В течение же этого временного интервала любые оценки VaR будут некорректны.
С помощью VaR оценивается вероятность возникновения потерь больше определенного уровня, то есть оценивается "вес хвоста" распределения, поэтому дополнительно к VaR рекомендуется изучать поведение портфеля в стрессовых ситуациях (Stress-testing) и использовать сценарный подход (Scenario Approach), чтобы оценить "длину хвоста" распределения.
К тому же VaR (как, впрочем, большинство известных методологий и методик) не дает абсолютной оценки возможных потерь, иногда VaR - "прогноз непрогнозируемых событий".
Однако VaR - действительно универсальный подход к оценке рыночных рисков, методология и элемент культуры современного риск-менеджмента.
Одна из главных целей разработки концепции VaR - одним единственным числом агрегировать и отобразить информацию о рыночных рисках портфеля, а также о рисках составляющих портфель сегментов и элементов.
Следует различать VaR как методологию, т.е. совокупность отдельных методов и методик оценки рыночного риска и числовые значения VaR для различных финансовых инструментов и всего портфеля в целом как суммы потенциально возможных потерь.
Теоретически рыночный риск может характеризоваться единственным параметром - VaR.
Например, при оценке валютных рисков открытых валютных позиций фирмы или коммерческого банка Value at Risk - выраженная в единицах базовой валюты суммарная оценка максимально возможных (с некоторой заданной вероятностью) убытков от воздействия того или иного рыночного фактора на открытую позицию по данному финансовому инструменту (впрочем, как и по портфелю в целом) в течение периода времени, необходимого для закрытия этой позиции.
Формализованно точное определение VaR портфеля активов (финансовых инструментов) часто формулируется следующим образом. Пусть портфель фиксирован (известна стоимостная структура портфеля: состав финансовых инструментов и их цены в момент времени t). VaR портфеля для заданного доверительного уровня и данного периода поддержания позиций Dt определяется как такое значение V, которое обеспечивает покрытие максимально возможных потерь DХ держателя (владельца или менеджера) портфеля за временной период Dt с заданной вероятностью р, т. е. выполняется соотношение: Р(DХ £ -V) = р.
С точки зрения теории вероятностей и математической статистики VaR соответствует р-квантилю заданного распределения. При этом VaR = V соответствует доверительному уровню (Confidence Level), равному 1 - p.
Проще говоря, VaR - статистическая оценка максимально возможных потерь данного портфеля финансовых инструментов при заданном распределении за определенный период времени во всех случаях, за исключением заранее заданного малого процента ситуаций.
Итак, VaR - величина максимально возможных потерь, такая, что потери в стоимости данного портфеля инвестора за определенный период времени с заданной вероятностью не превысят этой величины.
Таким образом, VaR дает вероятностную оценку потенциальных убытков по портфелю в течение определенного временного периода при экспертно заданном доверительном уровне. Доверительный уровень определяет вероятность наступления определенного события (например, 99% или 99,9%). Доверительный уровень часто соответствует доверительному уровню, используемому при расчете показателя отдачи на капитал RAROC (показатель «очищенной» от риска прибыли с капитала).
Доверительный уровень может устанавливаться не только в процентах, но и в среднеквадратических отклонениях (например, как в правиле "трех сигм" для гауссовского распределения вероятностей).
Временной горизонт определяет период, в течение которого осуществляется измерение риска потерь; он должен выбираться исходя из наличия статистических данных и характера проводимых операций в зависимости от продолжительности срока владения активами и ликвидности рынка.
В любом случае определение VaR подразумевает знание функции распределения доходности портфеля за выбранный интервал времени. Если стандартное отклонение как мера риска определяет "ширину" плотности распределения доходности портфеля, то VaR определяет конкретное значение потерь в стоимости портфеля, соответствующее заданному весу "хвоста" распределения.
Пример, поясняющий понятие и определение VaR, приведен на рис. 2.2.1. По оси абсцисс отложены изменения цен ликвидации портфеля в течение определенного периода времени, по оси ординат - частота появления этих изменений. Кривая на рисунке задает плотность распределения вероятностей прибылей и потерь для данного портфеля (часто не гауссовского распределения) и заданного периода поддержания позиций. Заштрихованная светлым область соответствует выбранному доверительному уровню 1 - р = 98,5% в том смысле, что ее площадь составляет 98,5% от общей площади под кривой; соответственно площадь затемненной области слева составляет 1,5% от общей площади под кривой. Таким образом, VaR представляет собой величину суммарных возможных потерь, отвечающих заданному доверительному уровню.
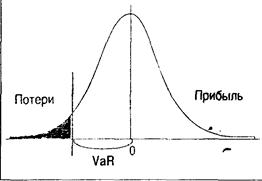
Рис.2.2.1.
Итак, для вычисления VaR необходимо определить ряд базовых элементов, непосредственно влияющих на его величину. В первую очередь это вероятностное распределение рыночных факторов, напрямую влияющих на изменения цен входящих в портфель активов. Понятно, что для его построения необходима некоторая статистика по поведению каждого из этих активов во времени. Если предположить, что логарифмы изменений цен активов подчиняются нормальному (гауссовскому) закону распределения с нулевым средним, то достаточно оценить только волатильность (здесь Volatility - среднеквадратическое отклонение приращения логарифма цены актива в единицу времени).
Однако на реальном российском финансовом рынке (впрочем, как и на многих зарубежных и международных рынках) предположение (гипотеза) о нормальности распределения, как правило, не выполняется.
После задания функций распределения рыночных факторов необходимо выбрать доверительный уровень, то есть вероятность, с которой наши потери не должны превышать VaR. Затем надо определить период поддержания позиций (holding period), на котором оцениваются потери. При некоторых упрощающих предположениях легко показать, что значение VaR портфеля пропорционально квадратному корню из периода поддержания позиций. Поэтому при принятии этих предположений или их достоверности достаточно вычислять только однодневную величину VaR. Тогда, например, четырехдневное значение VaR будет в два раза больше, а 25-дневное - в пять раз.
Кроме того, если в портфеле содержатся сложные производные финансовые инструменты (например, опционы), надо выбрать функцию их ценообразования в зависимости от параметров рынка. Наконец, необходимо определить корреляционные связи между различными рыночными факторами и составить матрицу ковариаций. Последнее представляется весьма важным.
Следует, однако, помнить, что любая числовая мера степени неопределенности является ограниченной - лишь само реальное распределение дает исчерпывающую характеристику риска. Поэтому в качестве такой меры риска выбор той или иной функции и числовых характеристик распределения должен производиться с учетом особенностей конкретной задачи управления рисками. Так, например, принимая доверительный уровень, скажем, 99%, мы должны подумать о последствиях "остального" 1% -будет ли это не слишком большой проигрыш порядка одного стандартного отклонения, или что-то типа мировых кризисов октября 1987 года (тогда индекс Доу-Джонса упал более чем на 800 пунктов) или 1997 года, "черного вторника" или кризиса августа 1998 года в России. В последних случаях необходимо увеличить доверительный интервал, например, до 99,9%-99,99%.
И, наконец, для расчета VaR необходимо знать стоимостную структуру портфеля (состав и цены финансовых инструментов).
Получение релевантной информации о составе портфеля - непростая задача. Некоторые крупные корпорации, имеющие в своем портфеле тысячи торгуемых на различных рынках инструментов и ведущие активные финансовые операции, сталкиваются с проблемой оперативного получения информации о текущей структуре портфеля.
Другая проблема состоит в выборе времени фиксации цен активов, образующих портфель. Торговые сессии на мировых рынках заканчиваются в разное время, что создает проблему: по каким ценам считать изменение стоимости портфеля? Обычно время фиксации выбирается как время закрытия торгов на рынке, где сосредоточены основные активы компании.
Итак, после того как выявлены все базовые элементы, следует обратиться непосредственно к процедуре вычисления Value-at-Risk.
Существуют три основных метода вычисления VaR: аналитический метод (иначе называемый вариационно-ковариационным методом, или методом ковариационных матриц), метод исторического моделирования (исторический метод, или метод исторических данных) и метод статистического моделирования (метод статистических испытаний или, иначе, метод Монте-Карло).
Основная идея аналитического метода заключается в выявлении рыночных факторов, влияющих на стоимость портфеля, и аппроксимации стоимости портфеля на основе этих факторов. То есть финансовые инструменты, составляющие портфель, разбиваются, насколько это возможно, на элементарные активы, такие, что изменение каждого зависит только от воздействия одного рыночного фактора. Например, многолетняя купонная облигация может рассматриваться как набор бескупонных облигаций с разными сроками погашения.
Портфель раскладывается на базисные активы (компоненты), от которых зависит его текущая (современная) стоимость (Present Value). Среднеквадратичное отклонение стоимости портфеля определяется среднеквадратическими отклонениями каждой из компонент и матрицей ковариаций. Наиболее известное воплощение этой модели - Risk-Metrics J.Р. Morgan.
Этот метод требует только оценки параметров распределения при явном допущении о виде распределения рыночных факторов. Обычно делают предположение о нормальном законе распределения каждого рыночного фактора. На основе данных прошлых периодов (далее исторических данных) вычисляются математические ожидания и дисперсии факторов, а также корреляции между ними. Если аппроксимация имеет линейный вид, то распределение доходности портфеля в целом также будет нормальным, и, зная параметры распределений рыночных факторов, можно определить параметры распределения всего портфеля.
Оценив стандартные отклонения логарифмов изменений цен для каждого из входящих в портфель активов, вычисляем VaR для них путем умножения стандартных отклонений на соответствующий доверительному уровню коэффициент. Полное вычисление VaR портфеля требует знания корреляционных связей между его элементами.
Аналитический метод может быть обобщен на портфель с произвольным числом различных активов - достаточно знать их волатильности и корреляции между ними. Волатильности важны при рассмотрении нелинейных инструментов. Корреляции между различными активами особенно важны при рассмотрении сложных портфелей - именно корреляция определяет характер неттирования прибылей/убытков между различными инструментами.
Серьезное преимущество этого метода состоит в том, что для большинства рыночных факторов все необходимые параметры нормального распределения хорошо известны. Отметим также, что оценка риска в рамках методологии VaR, полученная с помощью аналитического метода, совпадает с оценкой риска, предлагаемой современной портфельной теорией.
Аналитический метод прост в реализации и позволяет относительно быстро (возможно, даже в режиме реального времени) вычислять VaR практически на любых современных компьютерах. Но качество оценки ухудшается при увеличении в портфеле доли инструментов с нелинейными функциями выплат.
Кроме того, необходимость делать допущения о виде распределений для базовых активов является серьезным недостатком этого метода. Аналитический метод обладает также рядом не менее существенных недостатков. В частности, приходится опираться на весьма сомнительные гипотезы о нормальности распределения и стационарности нормального распределения, что делает метод мало пригодным для современных российских (и не только российских) условий. Метод неприменим для портфелей, состоящих из инструментов, стоимость которых зависит от базисных активов нелинейным образом, например, для портфелей, содержащих нелинейные финансовые инструменты типа опционов и так называемых кредитных деривативов (Credit Derivatives).
Резюмируя все вышесказанное по аналитическому методу, можно выделить основные положительные и отрицательные стороны применения аналитического метода для расчета VaR. Преимущества: простота и наглядность расчетов; возможность расчета совокупной величины VaR для линейных инструментов; доступность методических материалов. Недостатки: допущение о нормальном распределении; невозможность расчета VaR для нелинейных инструментов.
Следующий метод, который используется при вычислении VaR, - это метод исторического моделирования. Этот метод заключается в исследовании изменений стоимости портфеля за предыдущий исторический период. Исторические изменения стоимости активов используются для оценки изменения текущей стоимости портфеля. Определяются максимально возможные изменения стоимости портфеля для выбранного доверительного уровня.
Для вычисления VaR на определенный исторический период составляется база данных значений цен инструментов, входящих в портфель (или выделенных рыночных факторов, если портфель аппроксимируется). После этого надо вычислить изменения цен инструментов за промежуток времени, для которого рассчитывается VaR, и получить соответствующие значения изменений стоимости портфеля. Затем надо проранжировать полученные данные, построить гистограмму распределения изменений стоимости портфеля и найти значение VaR, соответствующее выбранному значению вероятности.
Этот метод является непараметрическим и основан на весьма понятном предположении о неизменности развития и стационарности рынка в ближайшем будущем. Выбирается период времени (например, 100 торговых дней), за который отслеживаются относительные изменения цен всех входящих в сегодняшний портфель активов. Затем для каждого из этих изменений вычисляется, насколько изменилась бы цена сегодняшнего портфеля, после чего полученные 100 чисел сортируются по убыванию. Взятое с обратным знаком число, соответствующее выбранному доверительному уровню (например, для уровня 99% необходимо взять число с номером 99), и будет представлять собой эмпирическую оценку VaR портфеля.
У исторического метода есть безусловные преимущества - он не требует серьезных упрощающих предположений и способен улавливать весьма неординарные события на рынке. Важные преимущества данного метода состоят также в том, что он свободен от предположений о виде распределения рыночных факторов портфеля, прост в осуществлении. При его использовании не возникает проблем с оценкой портфеля, содержащих опционы и подобные им инструменты.
К недостаткам обсуждаемого метода следует отнести то, что он требует проведения большой работы по сбору исторических данных и их обработке. Кроме того, оценка возможных изменений стоимости портфеля ограничена набором предыдущих исторических изменений. Типичная проблема при использовании данного метода состоит в отсутствии требуемого объема исторических данных. Чтобы получить более точную оценку VaR, необходимо использовать как можно больший объем данных, но использование слишком старых данных приводит к тому, что сегодняшний (и тем более будущий) риск будет оценен на основе данных, которые не соответствуют текущему состоянию рынка.
Таким образом, наиболее существенным недостатком исторического метода является его исключительная неустойчивость по отношению к выбору предыстории.
В самом деле, пусть портфель состоит только из одного фьючерса на доллар США. Пусть из доступных нам n дней периода предыстории в течение первых n/2 дней волатильность изменений цен фьючерса была равна 1%, а в течение последующих n/2 дней – в десять раз меньшее, чем при выборе всей доступной предыстории. Какое значение считать верным не понятно. Вопрос остается открытым, а ответ на него потребует дополнительных гипотез о текущем состоянии рынка.
Следующим на очереди является метод статистического моделирования (иначе метод Монте-Карло), который основан на моделировании случайных процессов с заданными характеристиками. Данный метод заключается в моделировании возможных изменений стоимости портфеля при некоторых предположениях. Выявляются основные рыночные факторы, влияющие на стоимость портфеля. Затем строится совместное распределение этих факторов каким-либо способом, например, с использованием исторических данных или данных, основанных на каком-либо сценарии развития экономики. После этого моделируется большое число возможных сценариев развития ситуации, а изменение портфеля считается для каждого результата моделирования. Далее строится гистограмма полученных данных и определяется значение VaR.
Таким образом, изменения стоимости портфеля моделируются на основе выбранных статистических параметров отдельных активов, входящих в состав портфеля.
В отличие от исторического моделирования в методе Монте-Карло изменения цен активов генерируются псевдослучайным образом в соответствии с заданными параметрами. Имитируемое распределение может быть в принципе любым, а число сценариев весьма большим (от нескольких десятков до сотен тысяч). В остальном этот метод почти аналогичен методу исторического моделирования.
Метод Монте-Карло является наиболее точным и надежным при рассмотрении нелинейных инструментов. Этот метод имеет еще несколько важных преимуществ. Он не использует конкретную модель определения параметров и может быть легко перенастроен в соответствии с экономическим прогнозом. Метод моделирует не конечную стоимость портфеля, а целые сценарии развития ситуаций, что позволяет отслеживать изменение стоимости портфеля в зависимости от пути развития ситуации.
Недостатки метода Монте-Карло – его медленная сходимость (это приводит к существенным затратам времени и вычислительных мощностей), сложность и трудоемкость расчетов.
Итак, метод Монте-Карло отличается высокой точностью и надежностью, пригоден практически для любых портфелей, но его применение требует качественной математической подготовки специалистов и достаточных компьютерных ресурсов для сложных вычислений.
Выбор одного из методов определения VaR зависит, прежде всего, от структуры портфеля, временных ограничений и технических возможностей, а также многих других условий и обстоятельств.
Поэтому, вообще говоря, сложно рекомендовать тот или иной метод вычисления VaR. Выбирая, какому из них отдать предпочтение, необходимо учитывать макро- и микроэкономическую ситуации, а также стратегические и тактические цели и задачи конкретной организации.
Конкретные модели расчетов VaR могут быть основаны на комбинации изложенных выше методов и их модификаций.
Выделим основные моменты данной главы, на которые нужно обратить внимание. Ожидаемая доходность служит мерой потенциального вознаграждения, связанного с портфелем. Стандартное отклонение рассматривается как мера риска портфеля. Ожидаемая доходность портфеля является средневзвешенной ожидаемой доходностью ценных бумаг, входящих в портфель. В качестве весов служат относительные пропорции ценных бумаг, входящих в портфель. Ковариация и корреляция измеряют степень согласованности изменений значений двух случайных переменных.
Одной из распространенных моделей по оценке рисков является VaR модель. VaR – величина максимально возможных потерь, такая, что потери в стоимости данного портфеля инвестора за определенный период времени с заданной вероятностью не превысят этой величины. Таким образом, VaR дает вероятностную оценку потенциальных убытков по портфелю в течение определенного периода при экспертно заданном доверительном уровне.
Похожие работы
... в последовательном и постепенном движении в направлении эффективного риск-менеджмента. При этом СУР необходима лизинговой компании для наиболее эффективной оценки и управления инвестиционными рисками, возникающими в деятельности компании. Разработка системы методов управления инвестиционными рисками невозможна без рассмотрения основных сложившихся методов управления рисками на каждом из этапов ...
... проблемные вопросы и предлагать выделение конкретных мероприятий (работ), направленные на устранение потенциальных рисков. 3.1.1 Указанная деятельность осуществляется на основе Плана стратегического развития Компании. Для исследования возможностей и целесообразности управления инвестиционными рисками по отдельным направлениям деятельности или отдельным лизинговым проектам в Компании организуются ...
... варианты развития внешней инвестиционной среды и уменьшить влияние негативных факторов на деятельность предприятия; • обеспечивает четкую взаимосвязь стратегического, тактического (текущего) и оперативного управления инвестиционной деятельностью предприятия; • отражает преимущества предприятия в конкурентном окружении; • определяет соответствующую политику инвестиционной деятельности в рамках ...
... отдельных показателей и весовые коэффициенты групп показателей должны периодически корректироваться экспертами. Только в этом случае возможна правильная оценка кредитоспособности заемщика и индивидуального кредитного риска банка. 2 УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ (НА ПРИМЕРЕ БАНКА “СЕВЕРНАЯ КАЗНА” ОАО) 2.1 Общая характеристика Банка “Северная казна” ОАО Банк «Северная казна» ОАО основан 09 ...
0 комментариев