Построение информационно-управляющей системы с элементами искусственного интеллекта

СУМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Кафедра автоматики и промышленной электроники

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

К курсовому проекту на тему: “ Построение информационно-управляющей системы с элементами искусственного интеллекта.”

По дисциплине: “Элементы систем автоматического контроля и управления.”

Проектировал:студент группы ПЭЗ-51 Симоненко А.В.

Проверил: Володченко Г.С.

Сумы 2000 г.

СОДЕРЖАНИЕ.

ВВЕДЕНИЕ.

1.СИНТЕЗ СИСТЕМЫ УПРАВЛЕНИЯ КВАЗИСТАЦИОНАРНЫМ ОБЪЕКТОМ.

Построение информационной управляющей системы с элементами самонастройки.

1.2 Построение логарифмических АЧХ и ФЧХ и нескорректированной системы

1.3. Построение желаемых ЛАЧХ и ФЧХ скорректированной квазистационарной системы.

1.4. Построение ЛАЧХ корректирующего звена системы.

2.СИНТЕЗ ИНФОРМАЦИОННО-ПАРАМЕТРИЧЕСКОЙ СИСТЕМЫ ИДЕНТИФИКАЦИИ НЕСТАЦИОНАРНОГО ОБЪЕКТА УПРАВЛЕНИЯ.

2.1. Выбор метода синтеза системы.

2.2. Поиск минимизированного функционала качества.

3.ПОСТРОЕНИЕ АДАПТИВНОЙ СИСТЕМЫ УПРАВЛЕНИЯ НЕСТАЦИОНАРНЫМ ДИНАМИЧЕСКИМ ОБЪЕКТОМ.

3.1. Синтез адаптивной системы управления нестационарным объектом с элементами искусственного интеллекта.

ЗАКЛЮЧЕНИЕ.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ.

ВВЕДЕНИЕ.

При современном уровне развития науки и техники все большее распространение получают информационно-управляющие системы с элементами искусственного интеллекта на производстве, в быту, военной технике, а также там , где присутствие человека невозможно.Их особенностью является наличие в самой системе подсистем анализа и контроля состояния как самой системы управления так и состояния объекта управления с целью своевременного принятия решения и реагирования на внешние воздействия и изменения в самой системе.

Системы автоматического контроля и управления должны обеспечить требуемую точность регулирования и устойчивость работы в широком диапазоне изменения параметров.

Если раньше теория автоматического управления носила в основном линейный и детерминированный характер, решаемость теоретических задач определялась простотой решения, которое стремились получить в виде замкнутой конечной формы, то в настоящее время решающее значение приобретает четкая аналитическая формулировка алгоритма решения задачи и реализация его с помощью ЭВМ.

1.СИНТЕЗ СИСТЕМЫ УПРАВЛЕНИЯ КВАЗИСТАЦИОНАРНЫМ ОБЪЕКТОМ

1.1Построение информационной управляющей системы с элементами самонастройки.

Для нестационарного динамического объекта управления, поведение которого описывается нестационарными дифференциальными уравнениями вида (1.1):

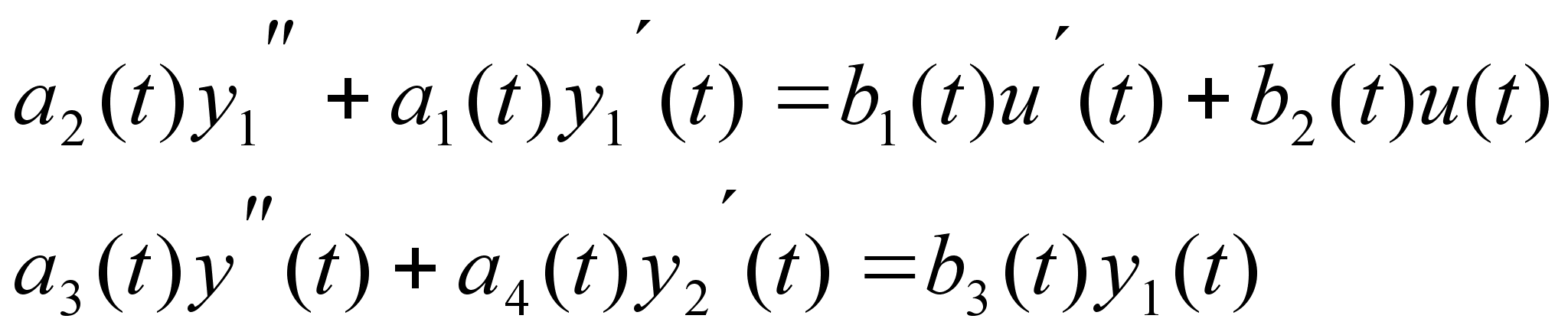
введем условие квазистационарности на интервале

(1.2)

(1.3)

Для решения задачи представим объект управления в пространстве состояний, разрешив систему (1.1) относительно старшей производной:

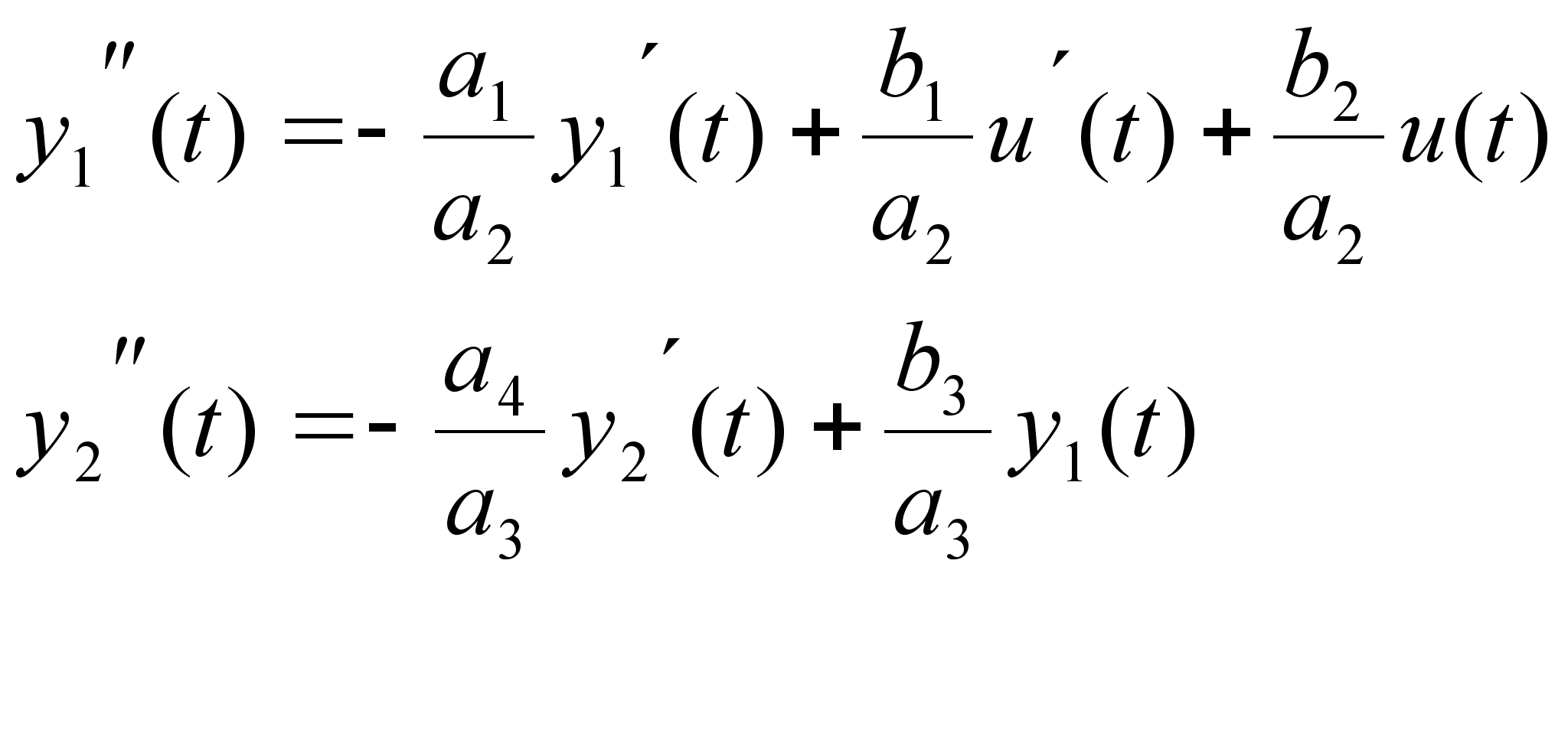
(1.4)

Полученная система уравнений описывает структуру объекта управления в пространстве состояний. Соответствующая структурная схема представлена на рисунке 1.

Y1’’(t)

Y1’(t)

U(t)

U(t)

U’(t)

Y1(t)

Y2’’(t)

Y2’(t)

Y2(t)

Рис.1

Представим схему переменных состояний в форме Коши. Для этого введем переобозначение через z.

Пусть (1.5) :

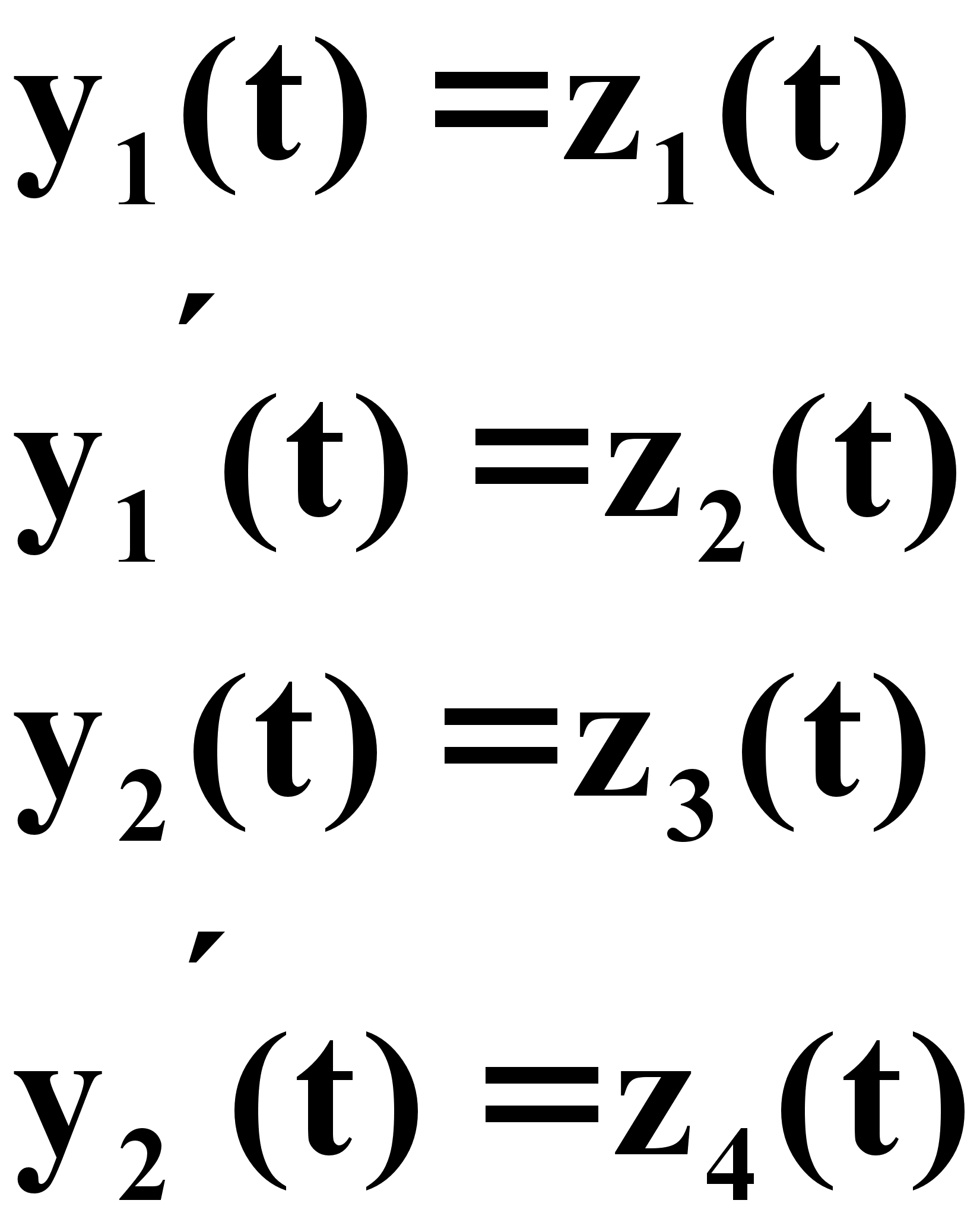
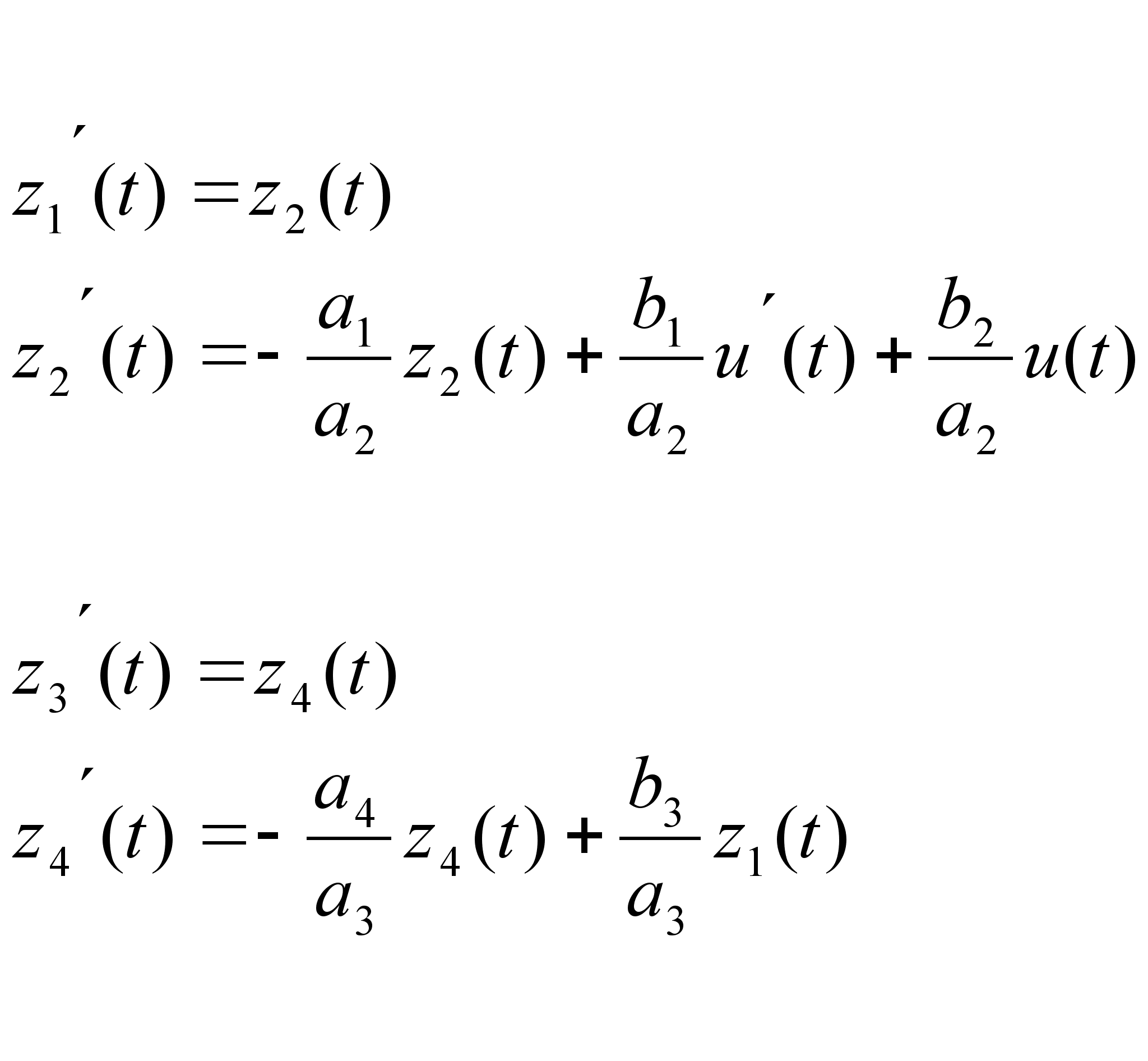
Система (1.5)-математическая модель объекта управления в форме Коши. Представим (1.5) в векторной форме:

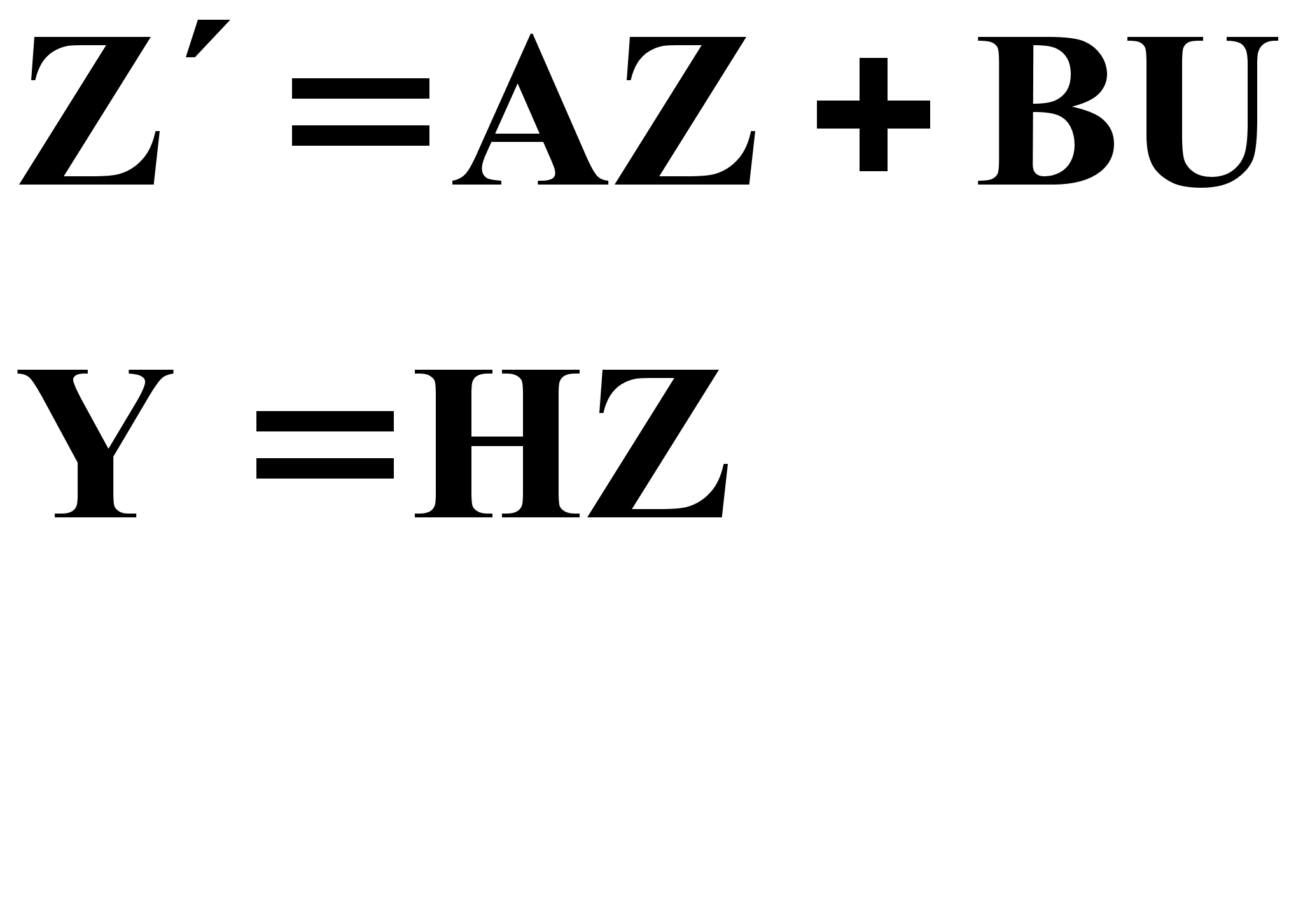(1.6)

где

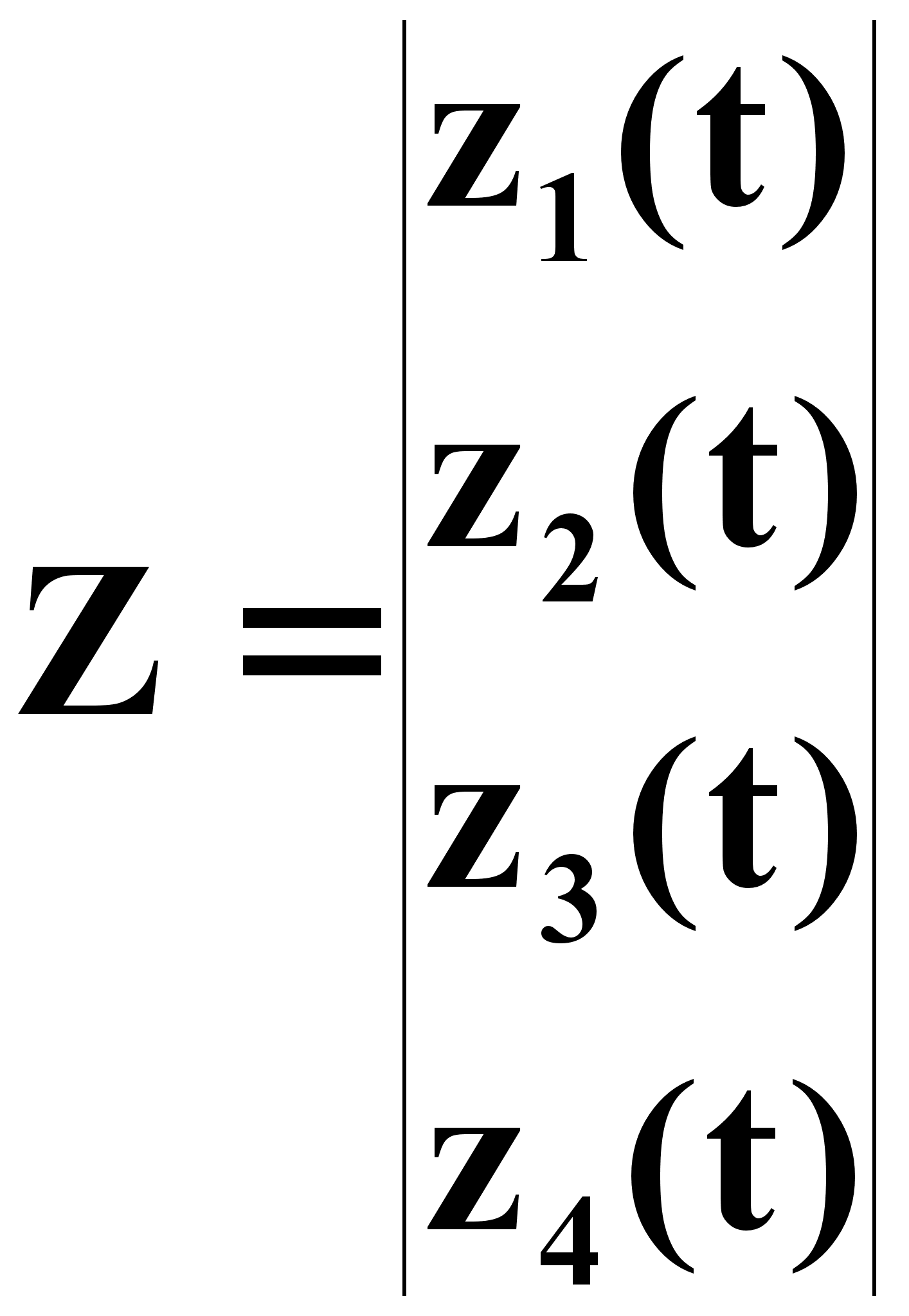вектор состояний (1.7)

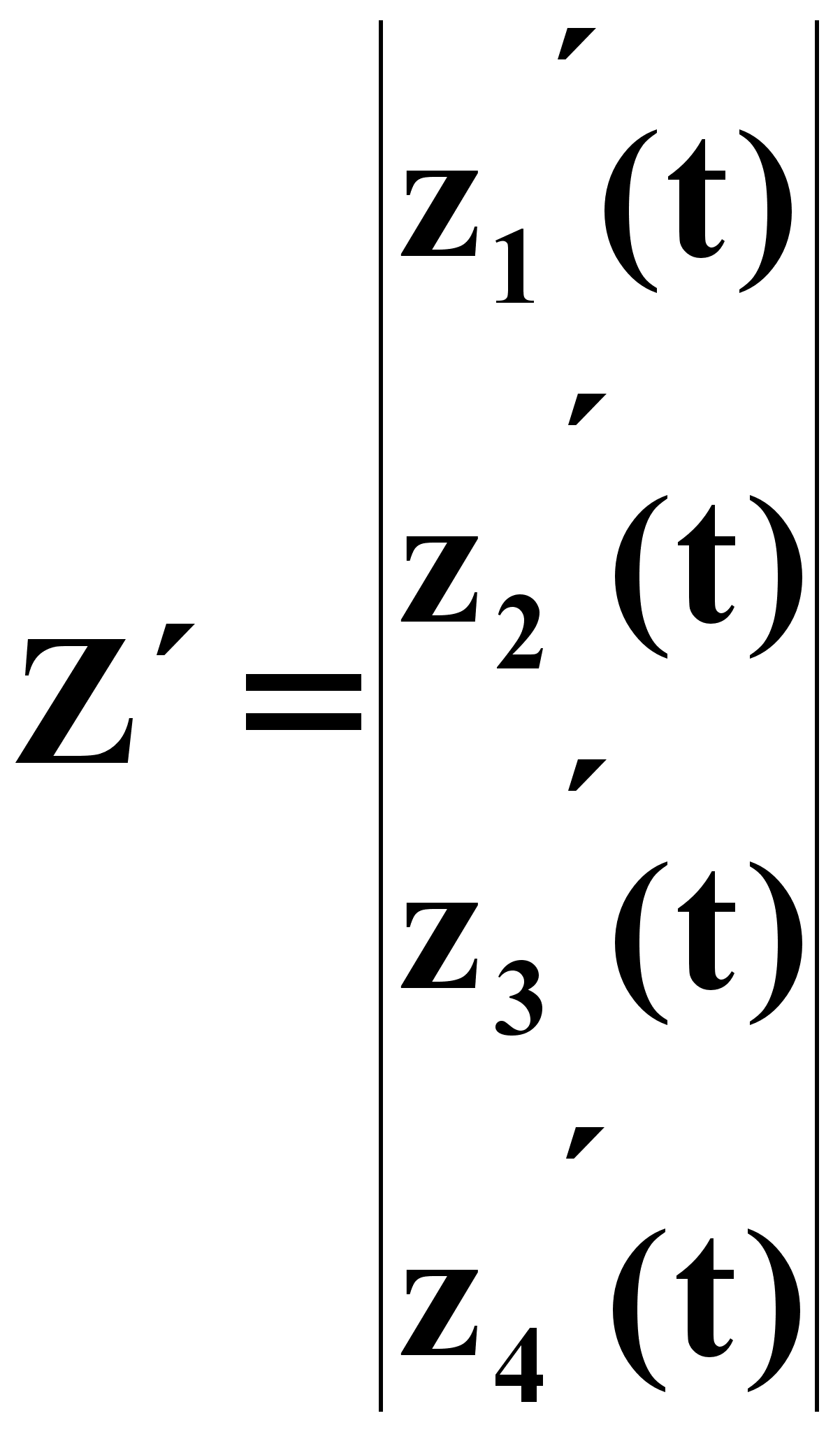производная вектора состояний (1.8)

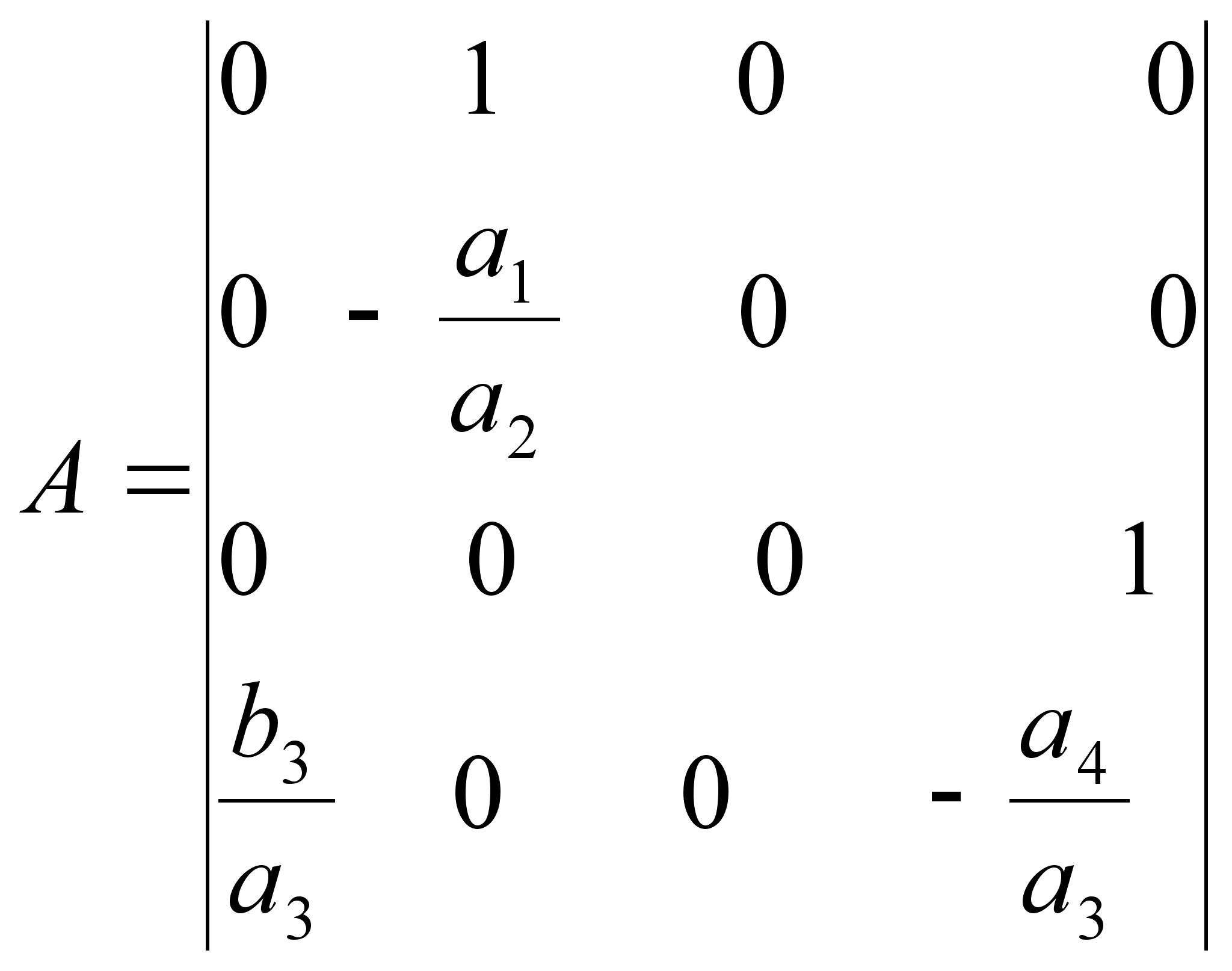динамическая матрица о/у (1.9)

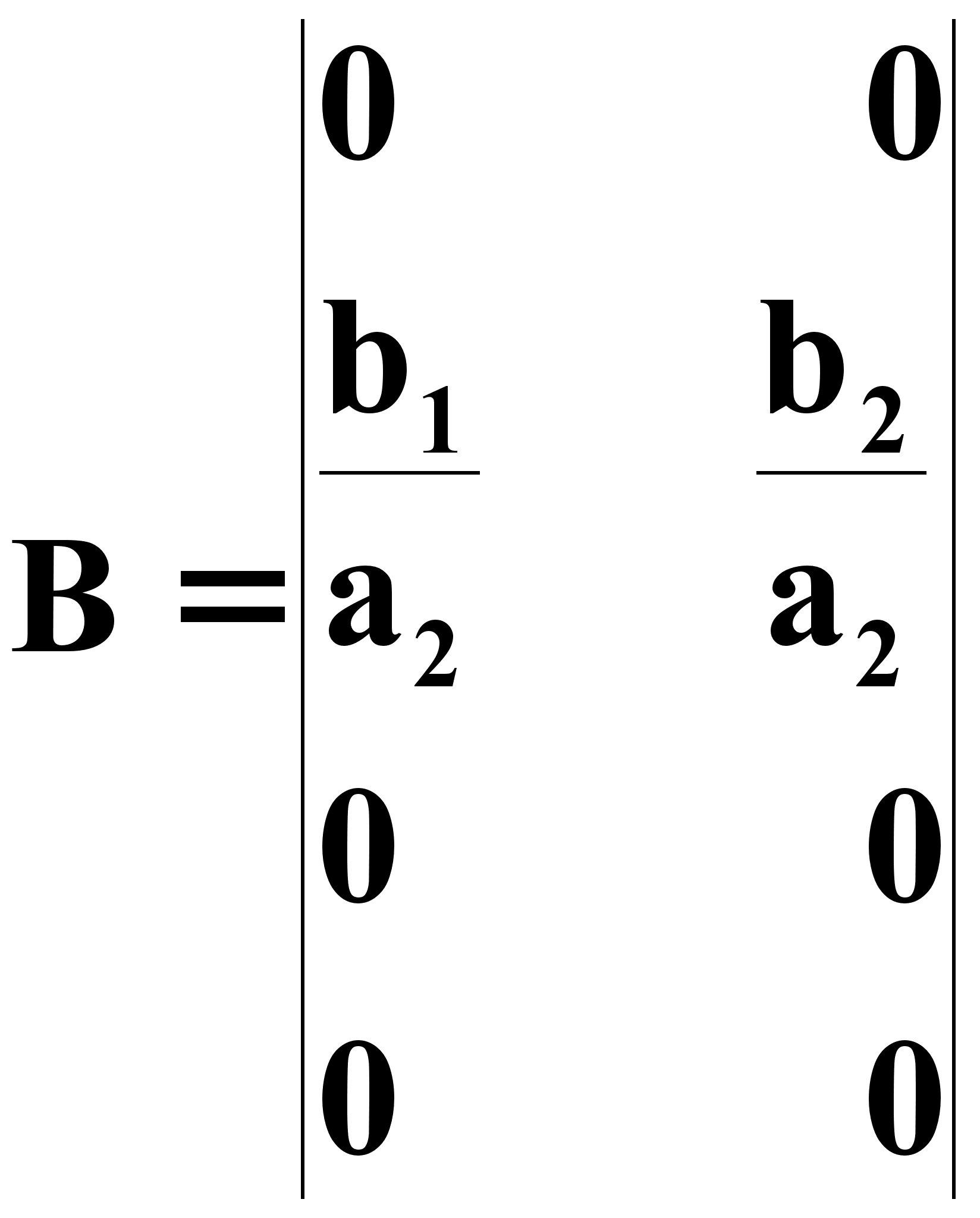матрица управления о/у (1.10)

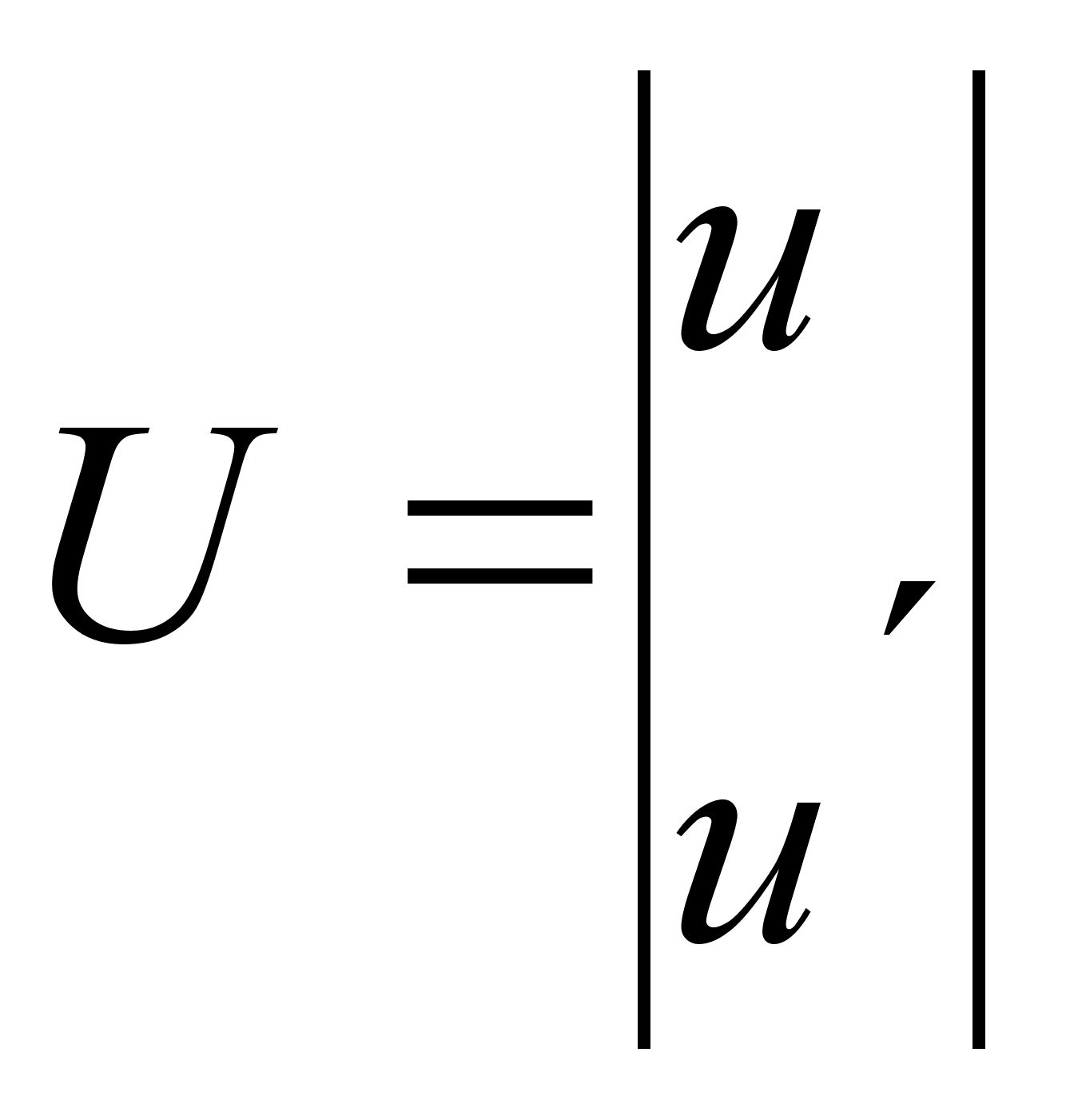вектор управляющих воздействий (1.11)

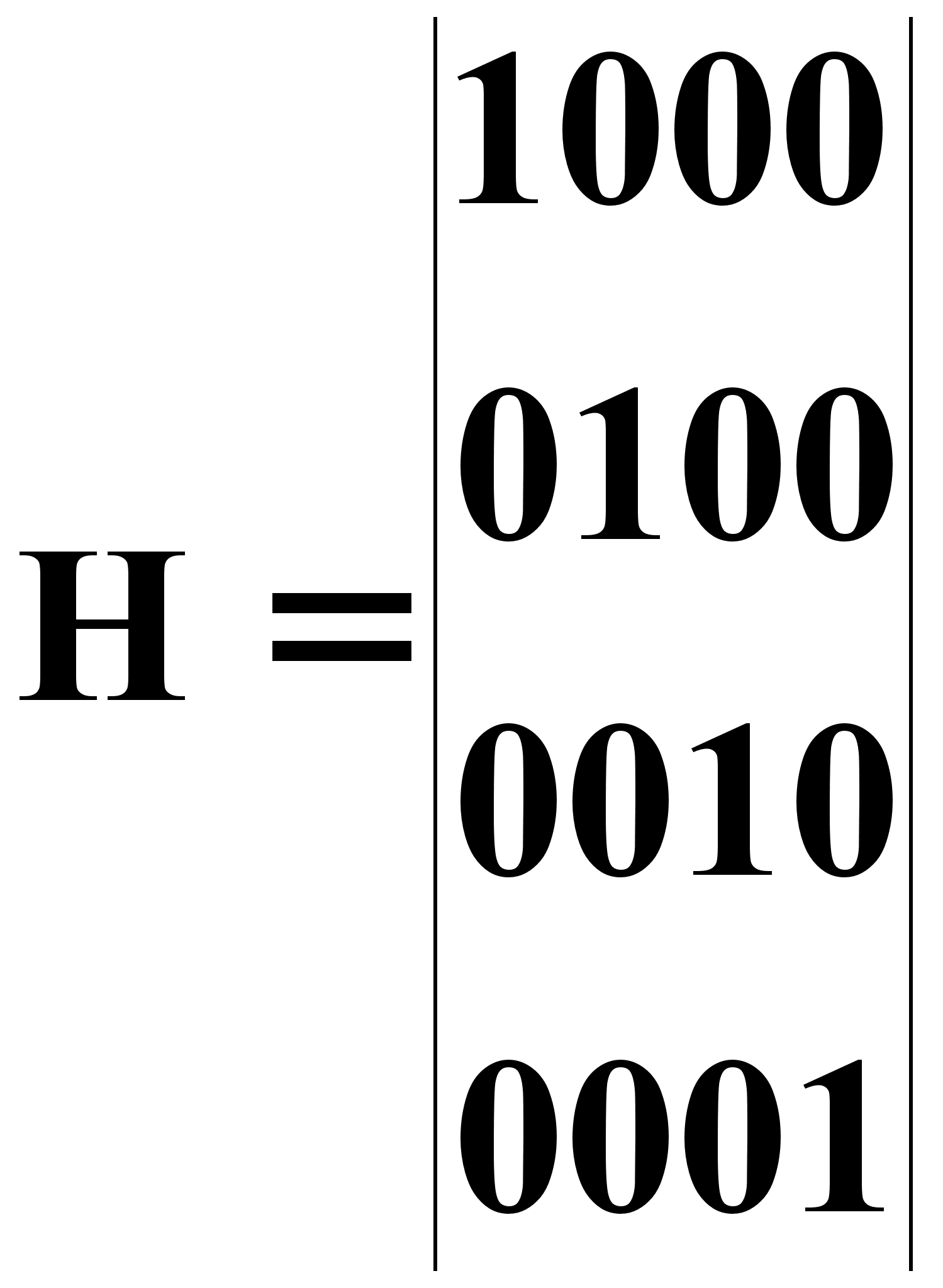матрица измерений (1.12)

Определяем переходную матрицу состояний в виде:

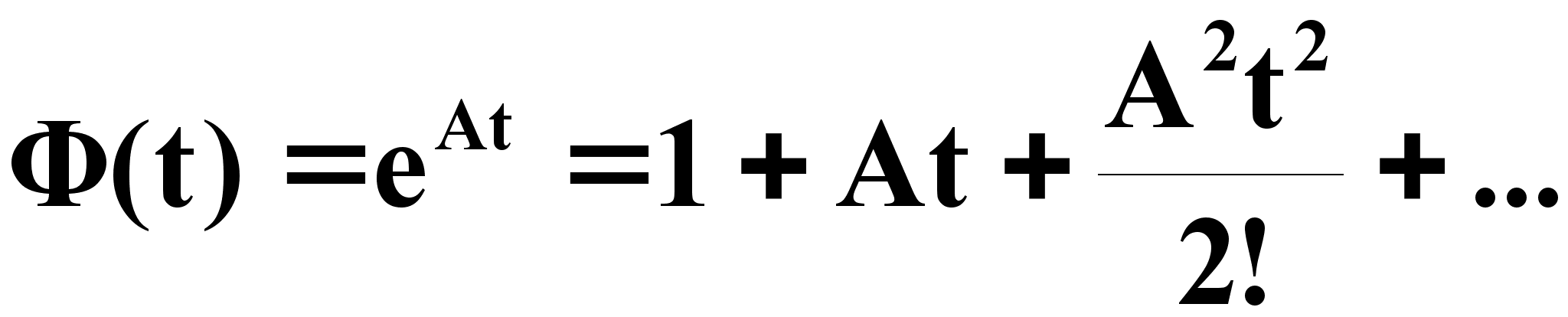
Находим передаточные функции звеньев системы управления, для чего представляем систему дифференциальных уравнений (1.1) в операторной форме:

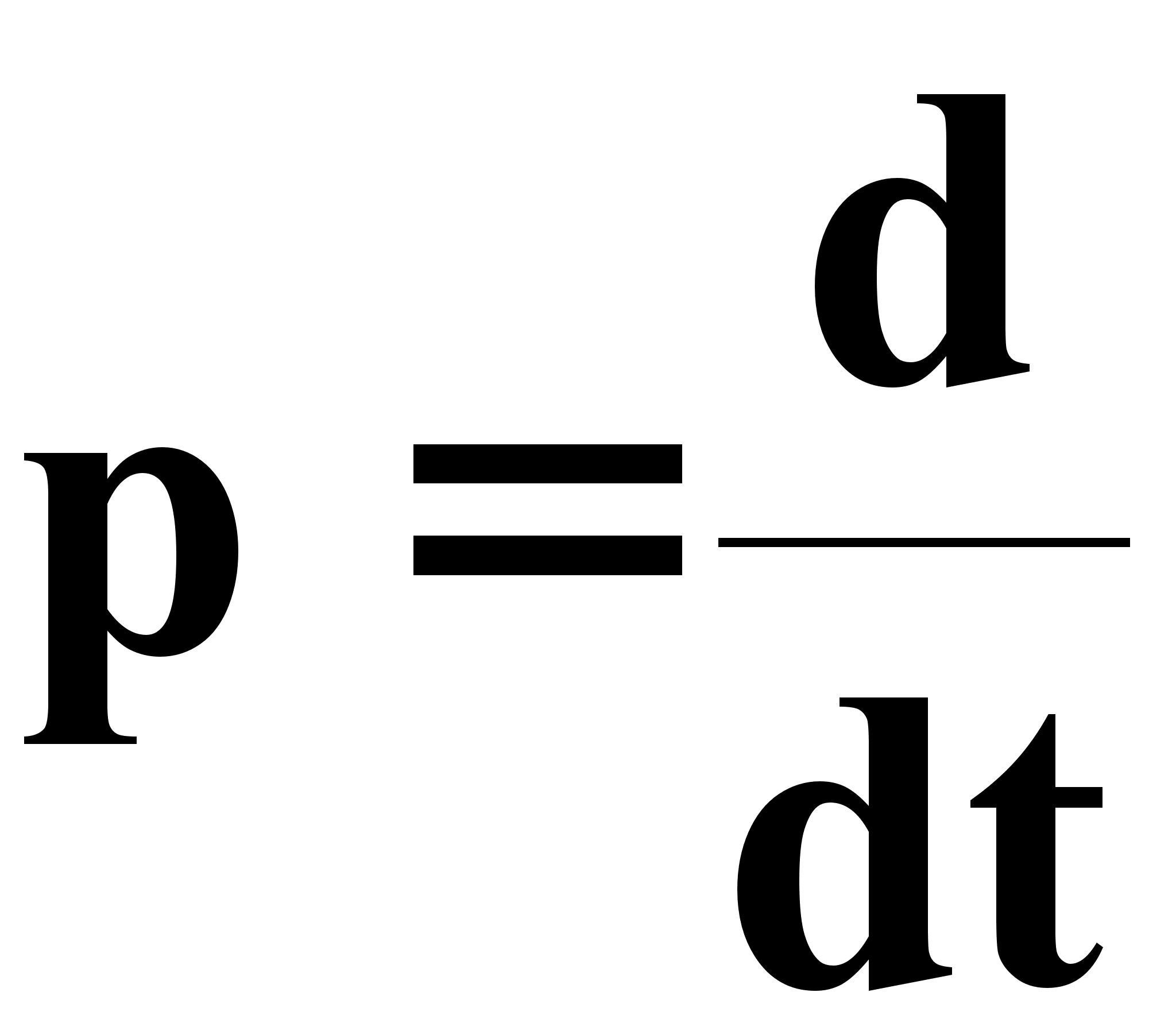(1.13)

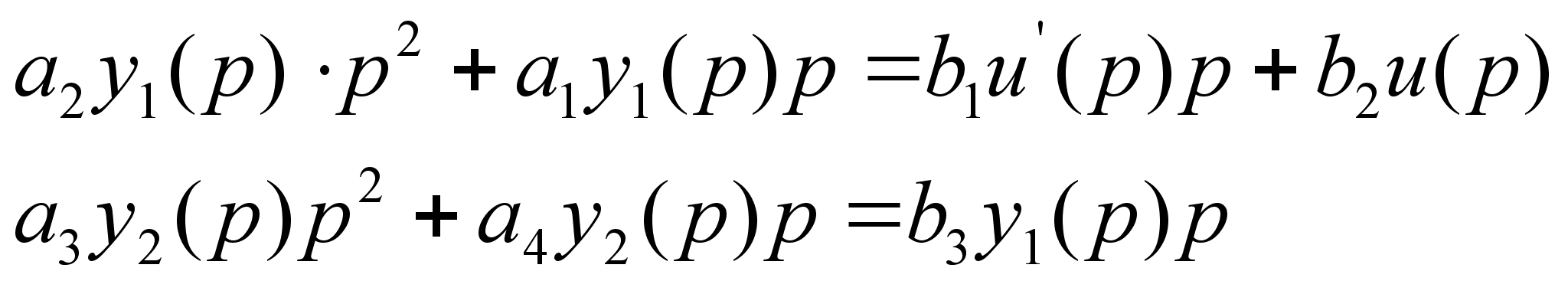
(1.14)

Вынесем общий множитель за скобки

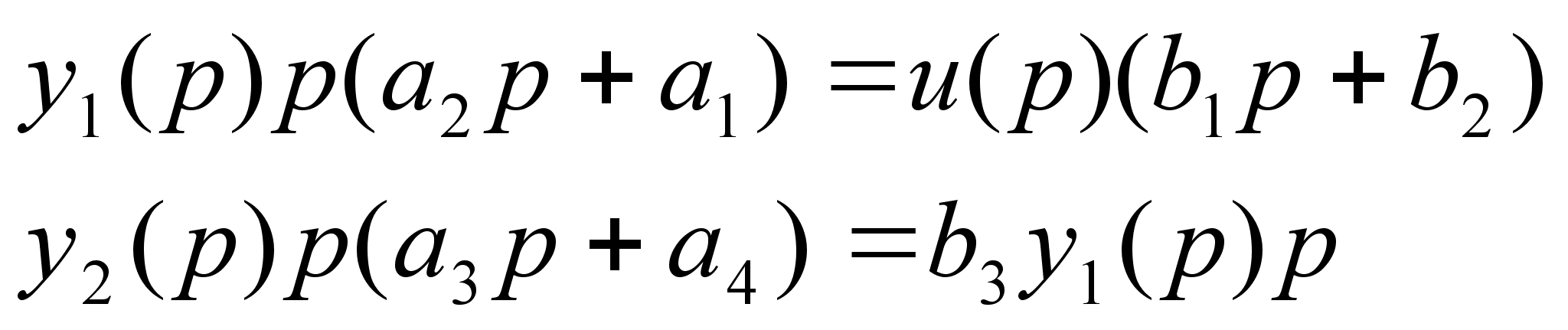(1.15)

Передаточная функция первого звена

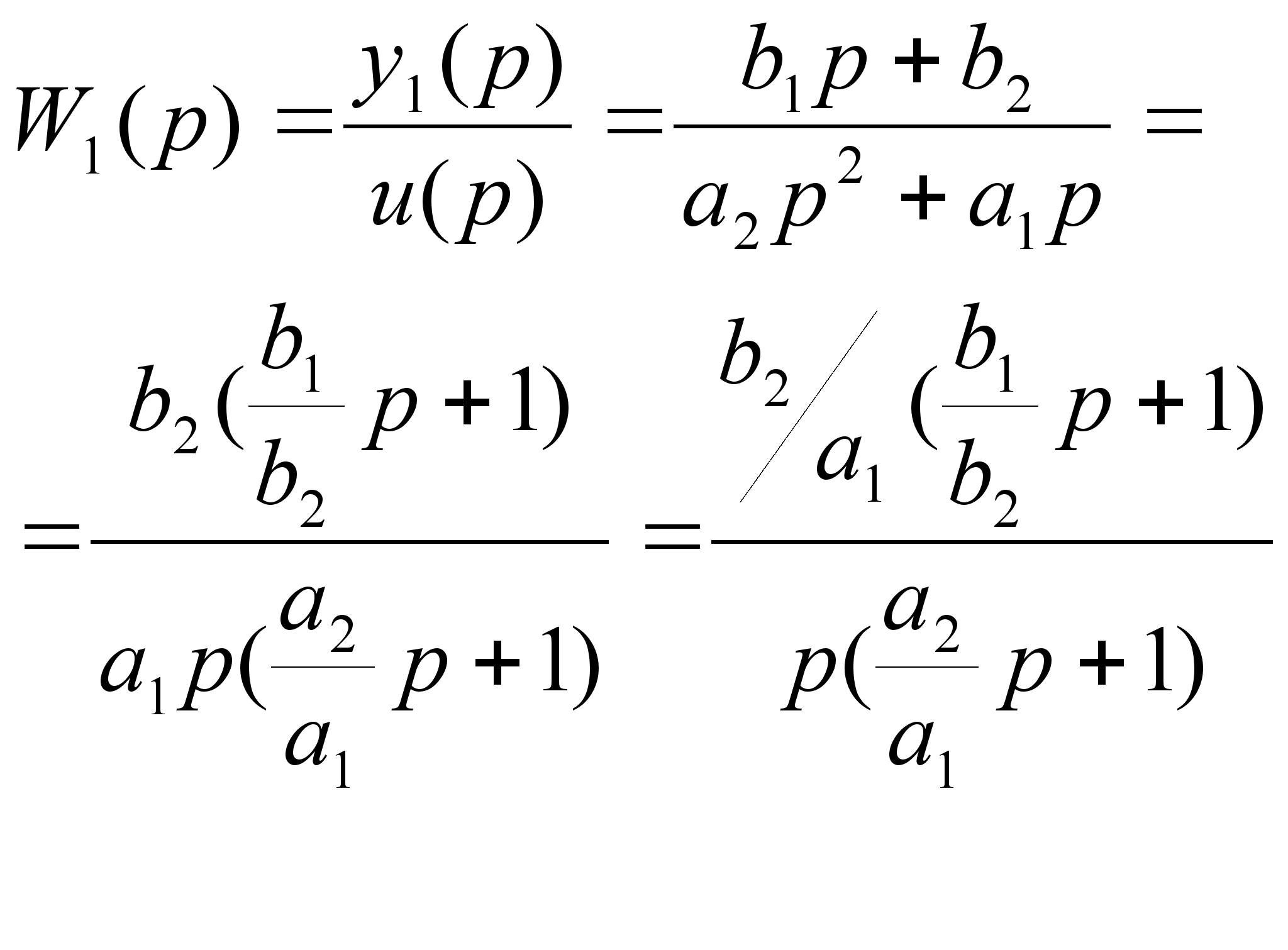
где

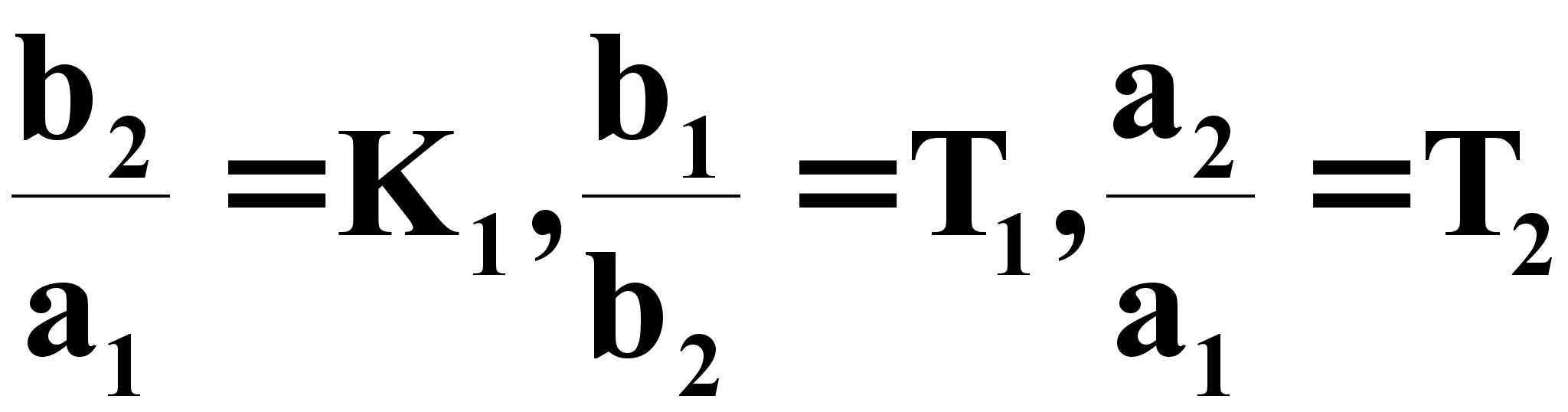
тогда

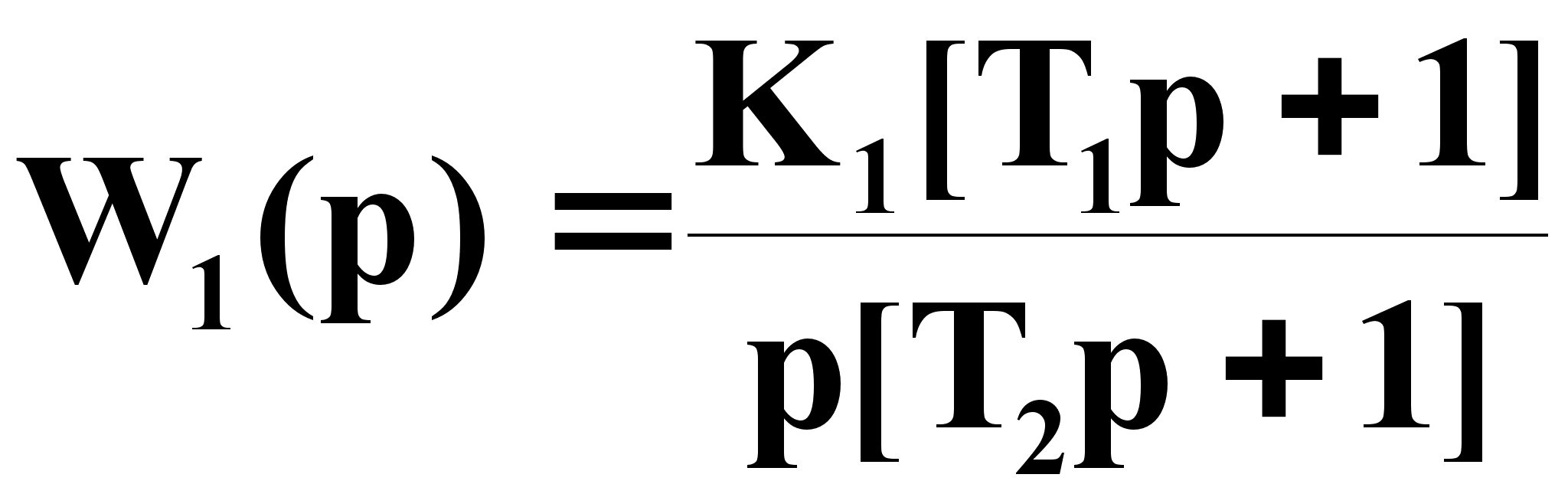(1.16)

Подставляем численные значения(см.т/з):

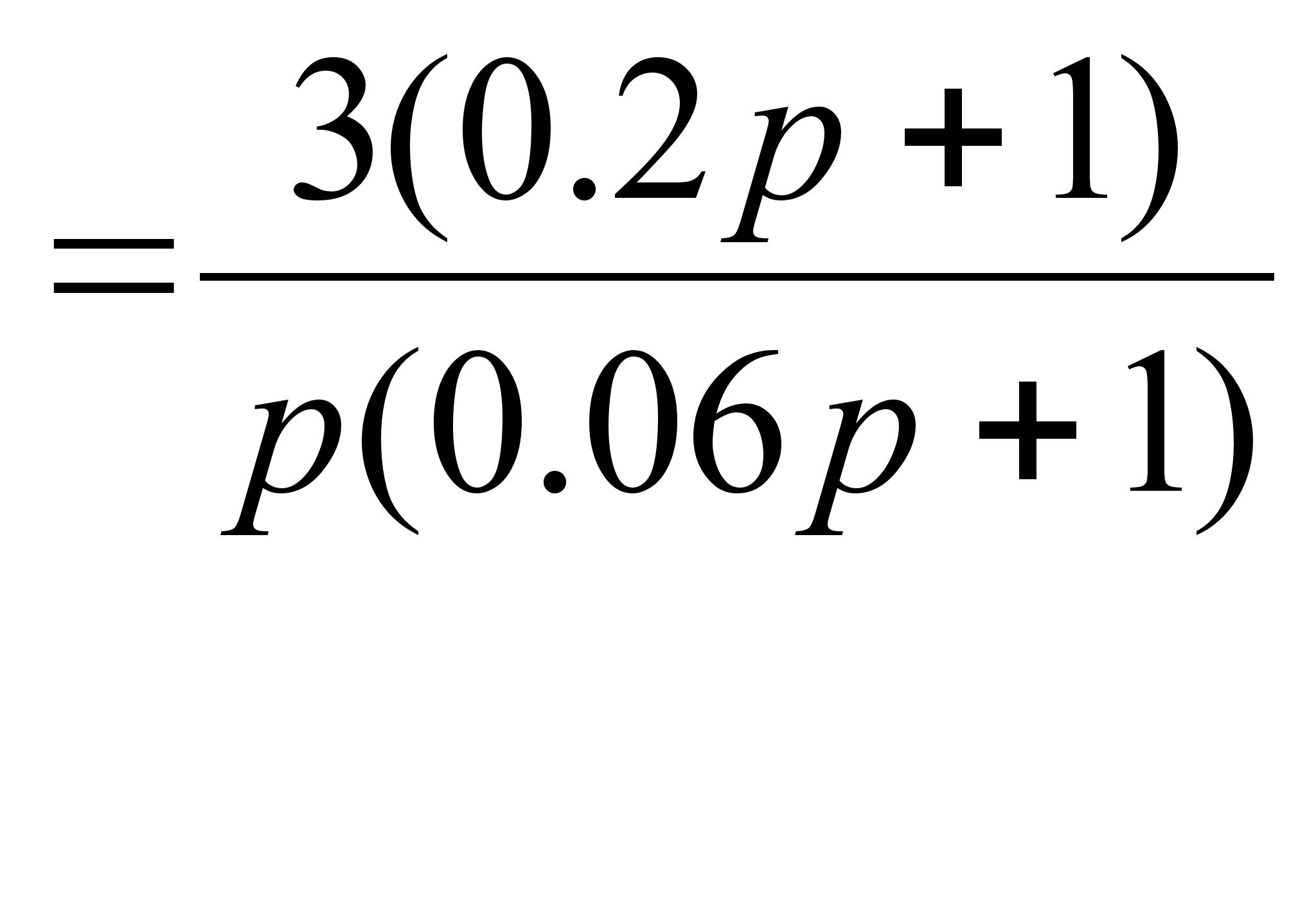
Передаточная функция второго звена:

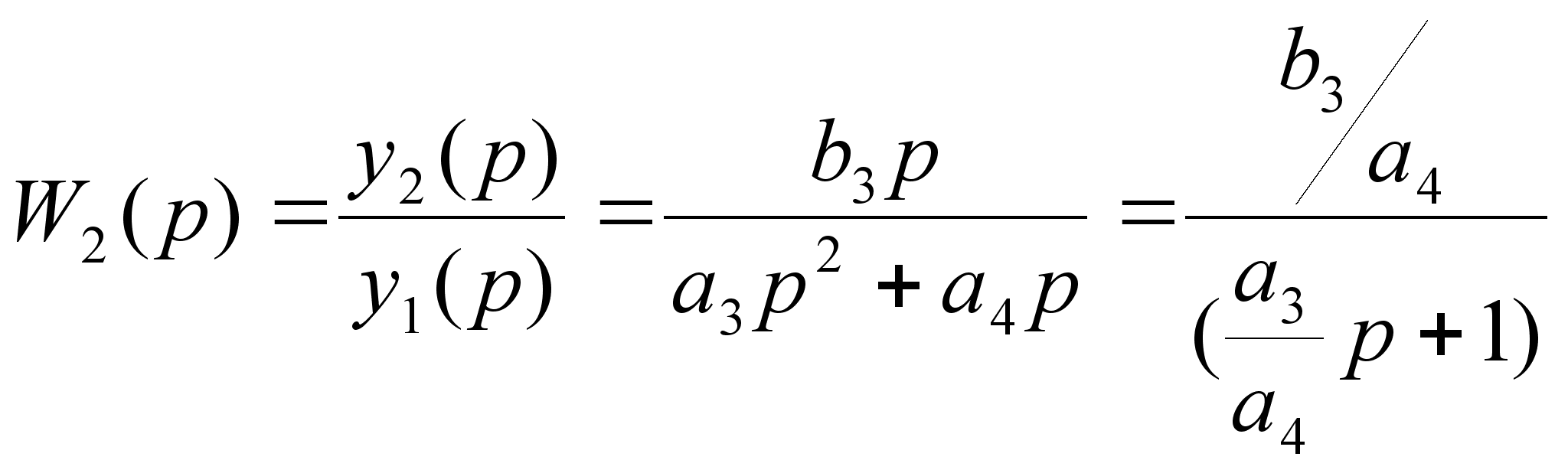
где

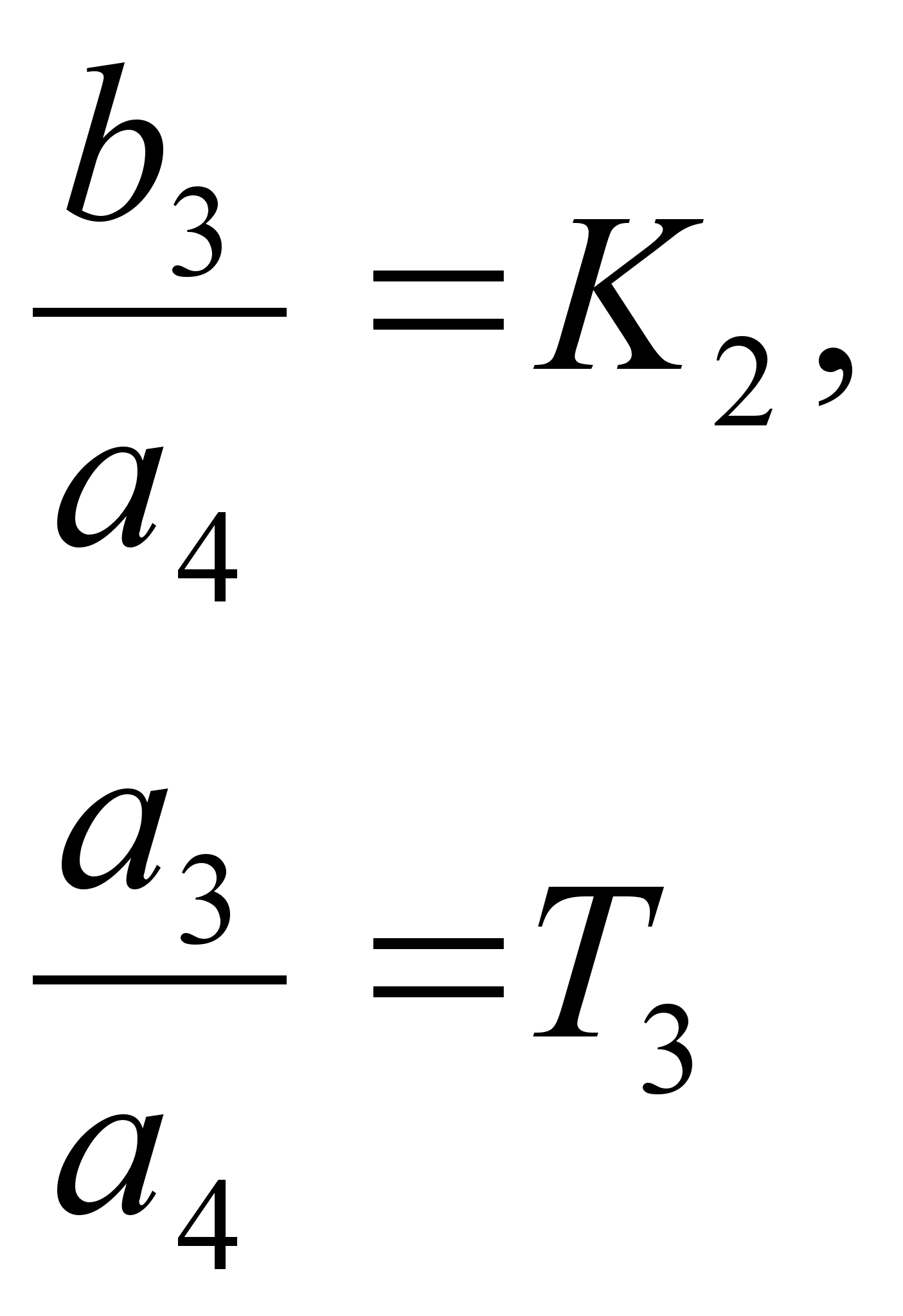
тогда

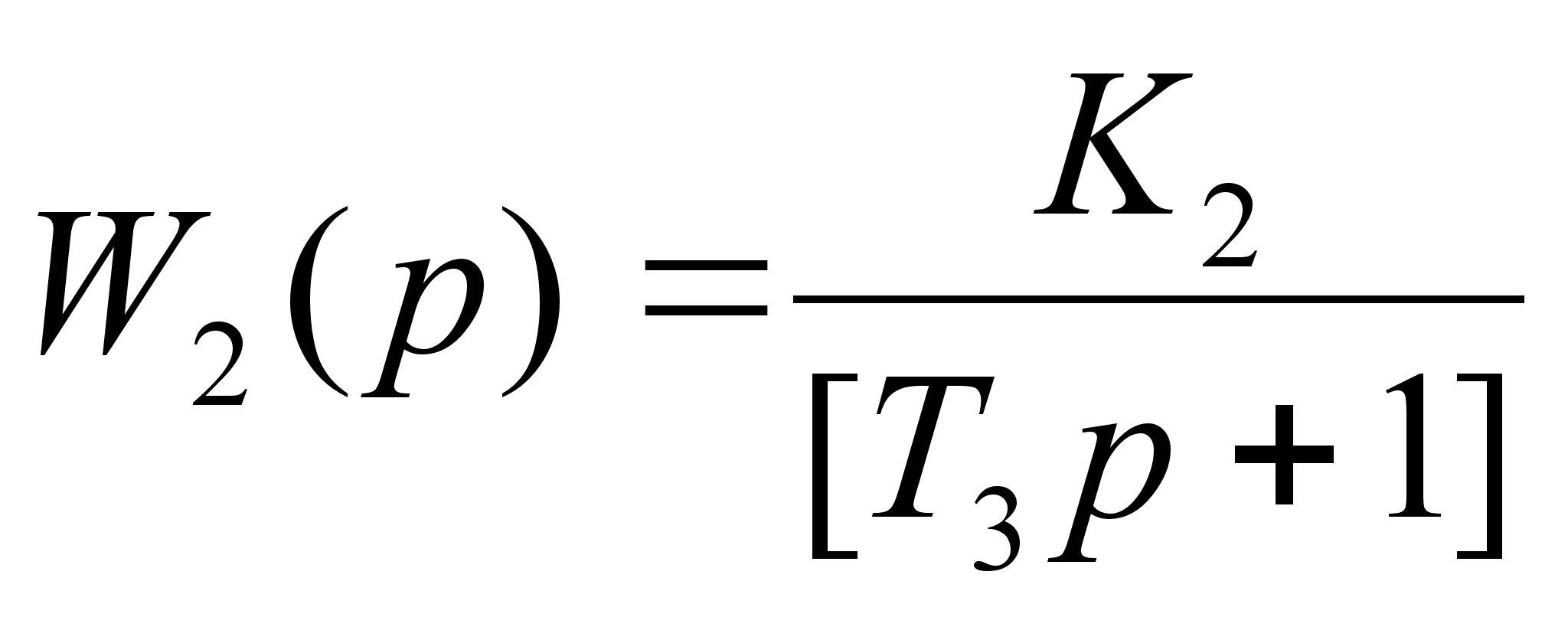(1.17)

Подставляем численные значения:

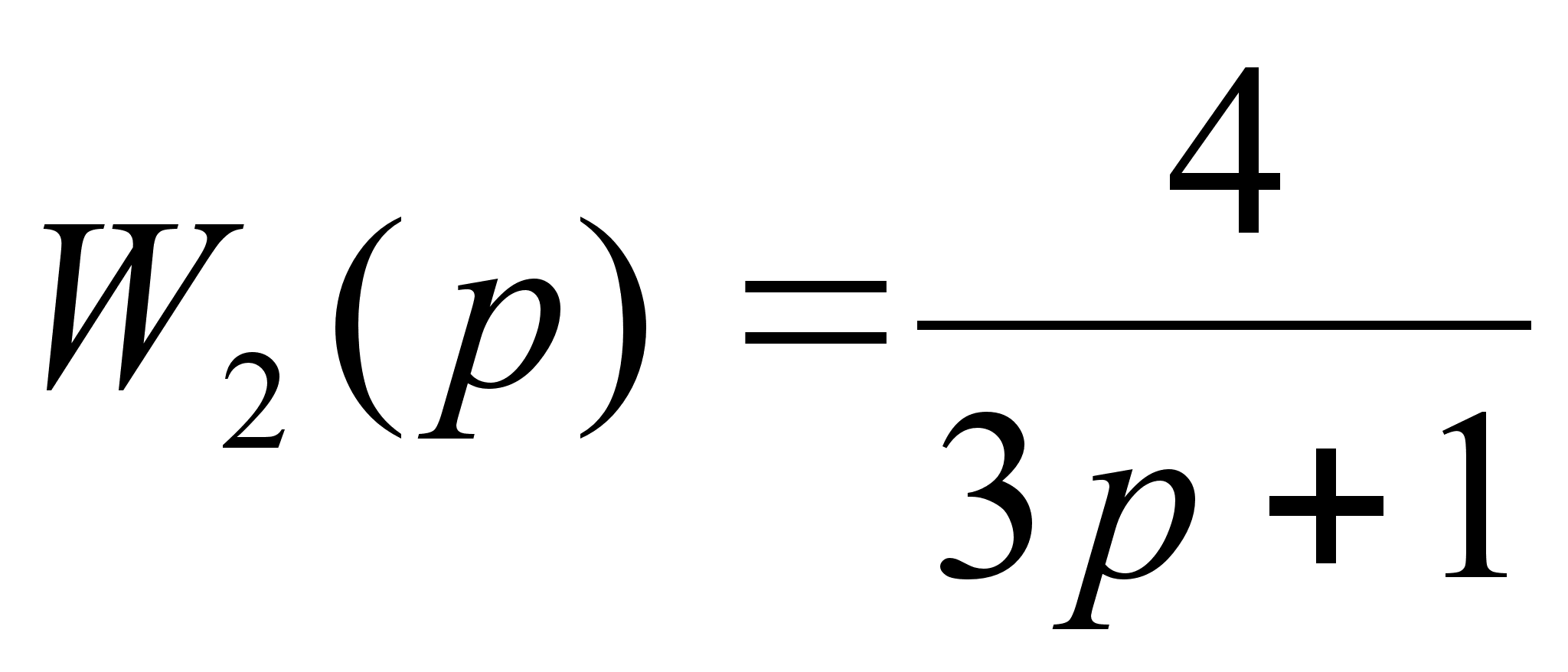
Используя заданный коэффициент ошибки по скорости, находим требуемый коэффициент усиления на низких частотах:

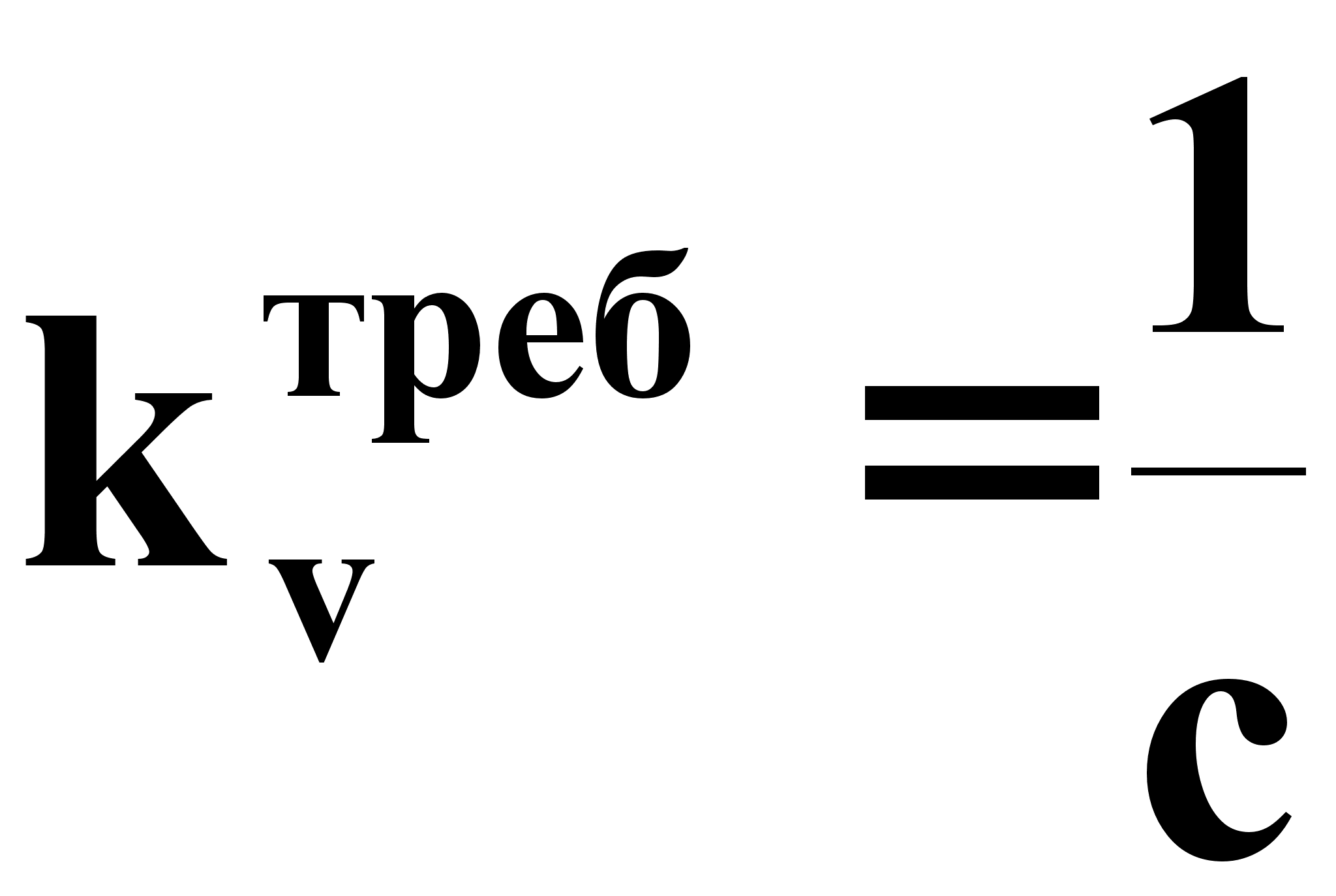(1.18)

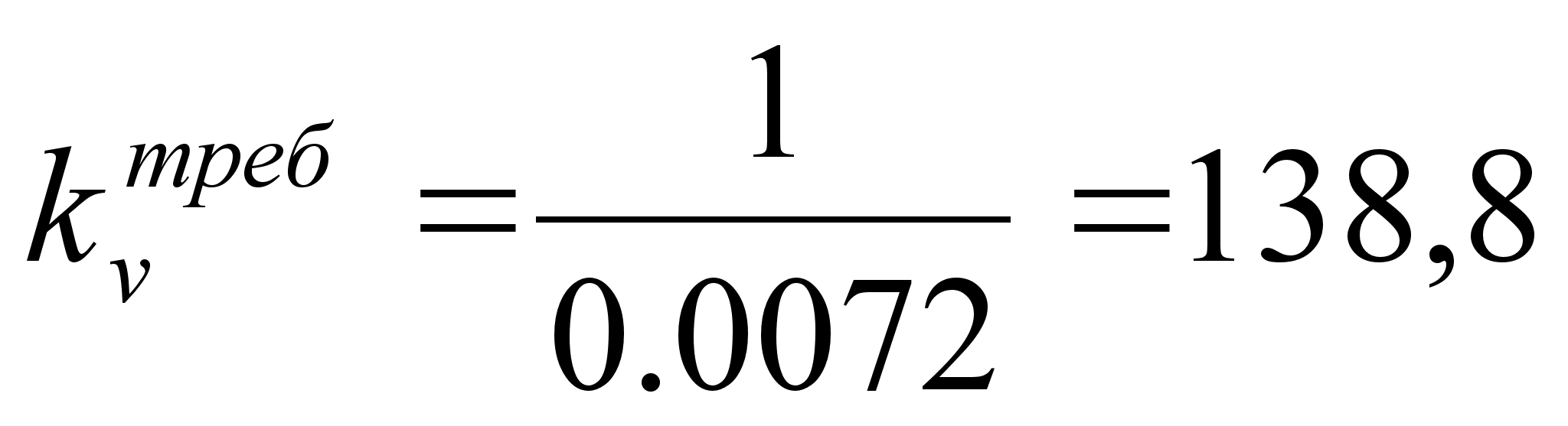
Для обеспечения требуемого коэффициента усиления вводим пропорциональное звено с коэффициентом усиления , равным

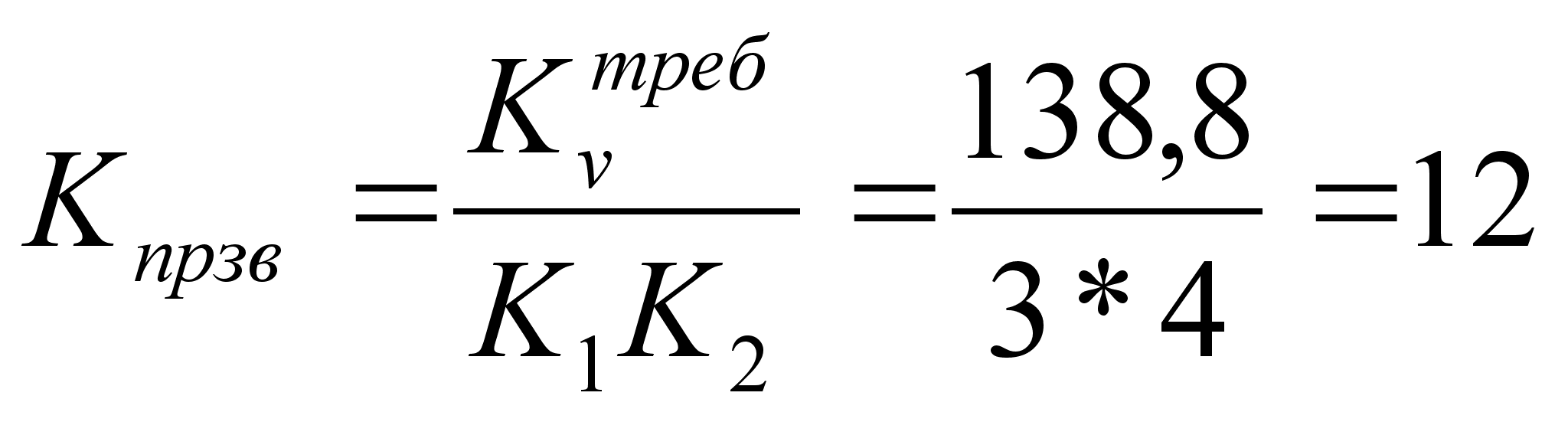
Передаточная функция системы численно равна:

(1.19)

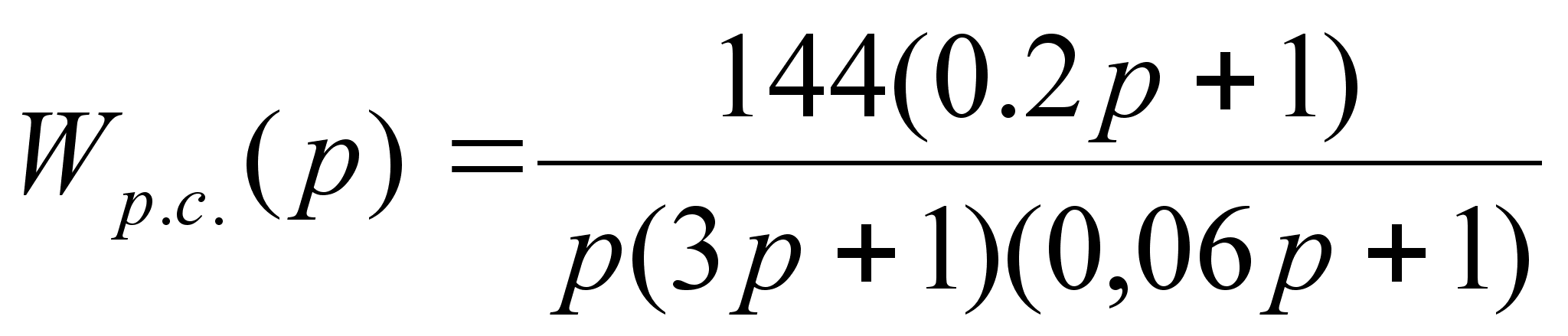
Построение логарифмических АЧХ и ФЧХ нескорректированной системы.

Заменив в выражении (1.19) , получим комплексную амплитудно-фазочастотную функцию разомкнутой системы:

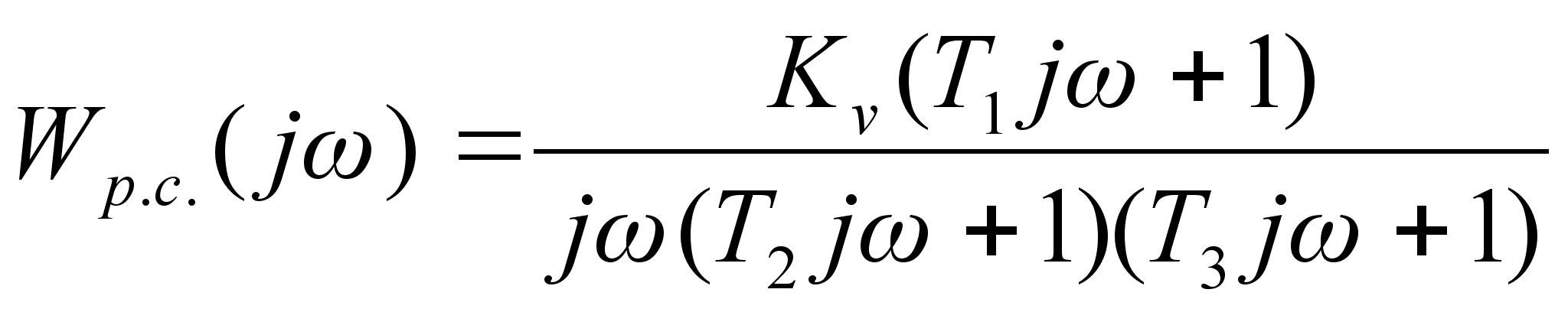(1.20)

Представим (1.20) в экспоненциальной форме:

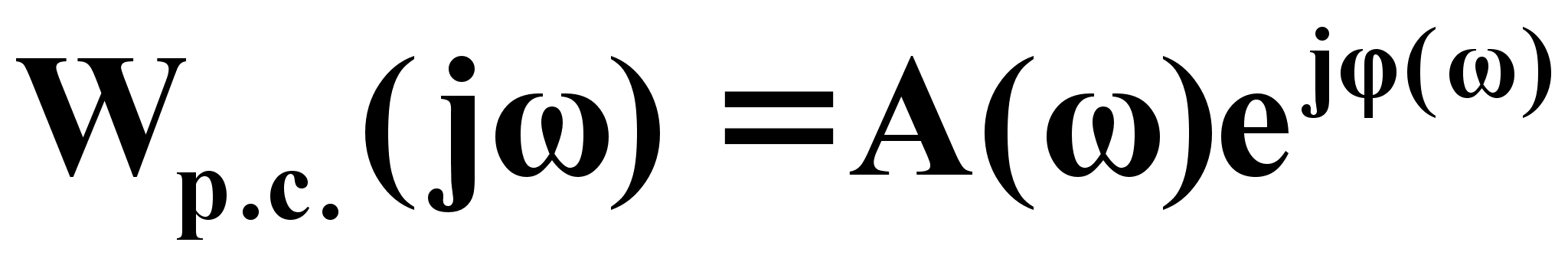(1.21)

Здесь

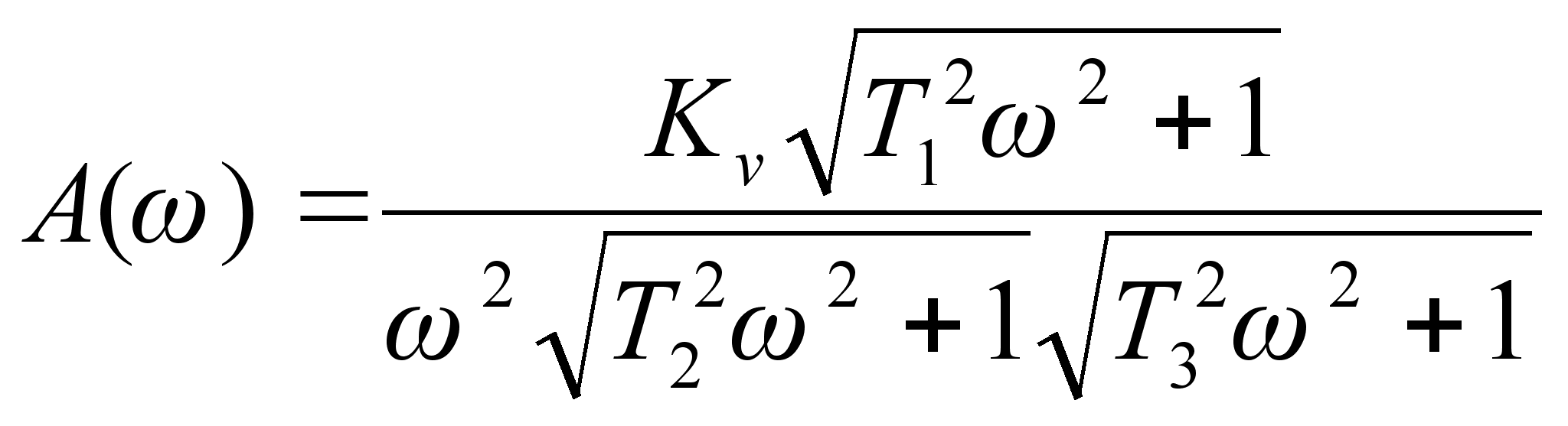(1.22)

(1.23)

Логарифмируем выражение (1.22):

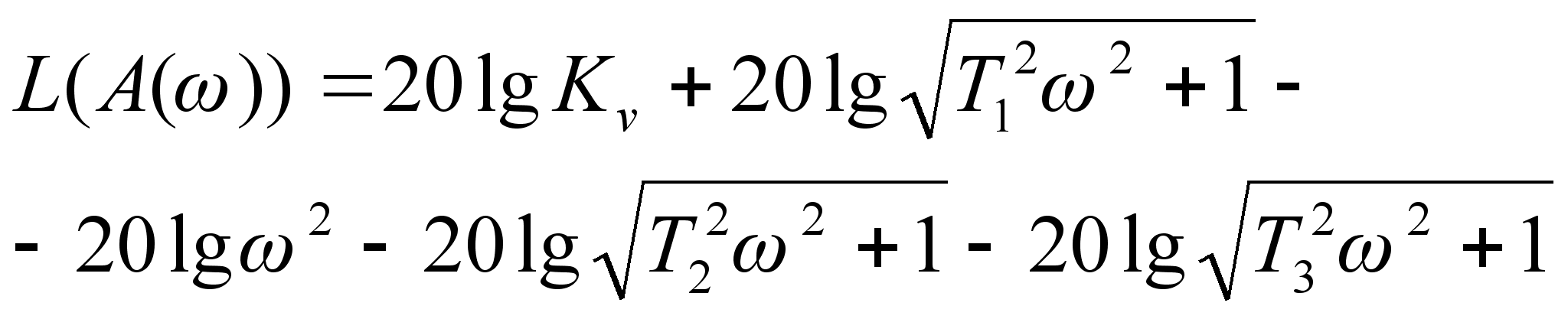(1.24)

Слагаемые 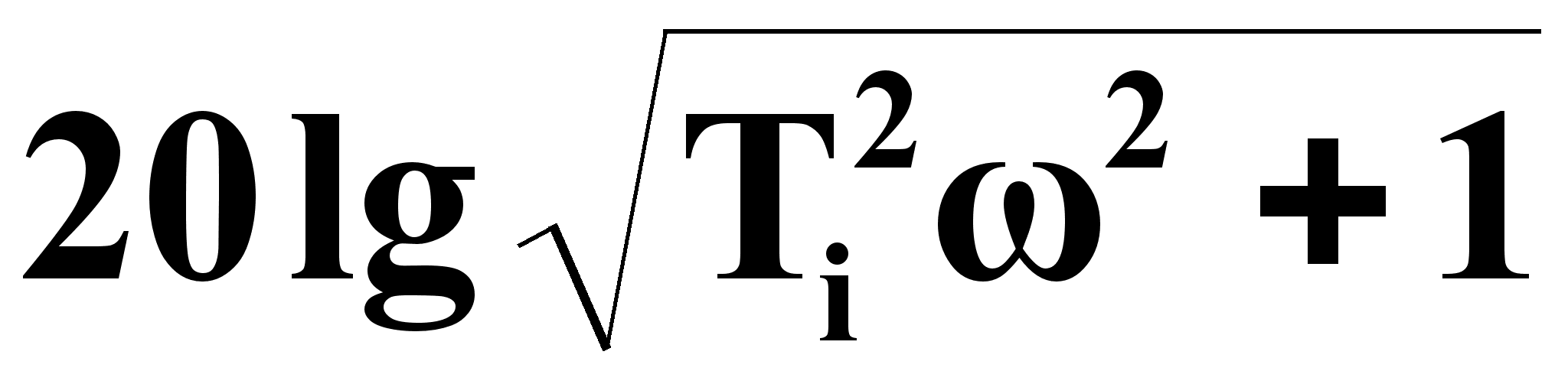на частотах

равны нулю, а на частотах принимают значения .

Соответственно, тогда логарифмическая амплитудно-частотная характеристика определяется выражением:

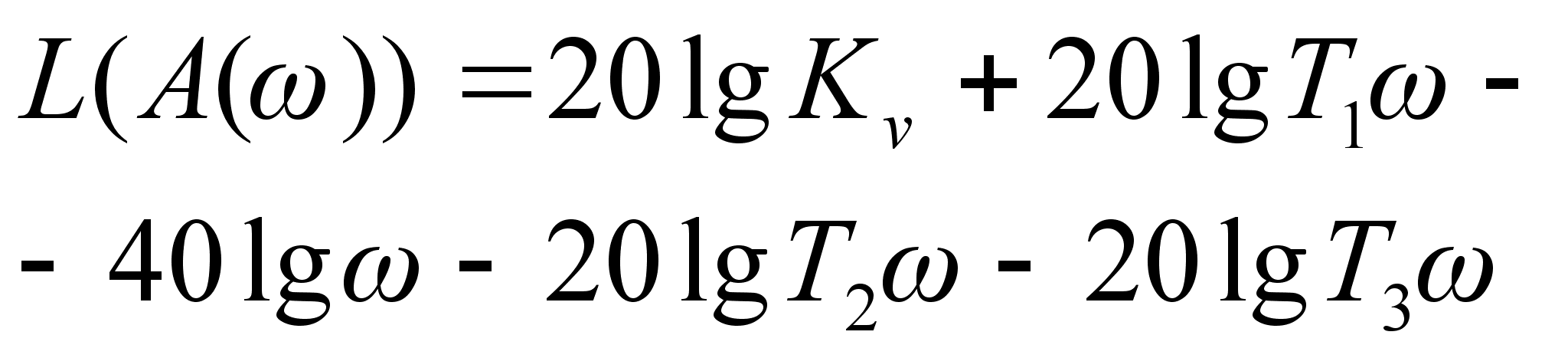(1.25)

Определим частоты сопряжения:

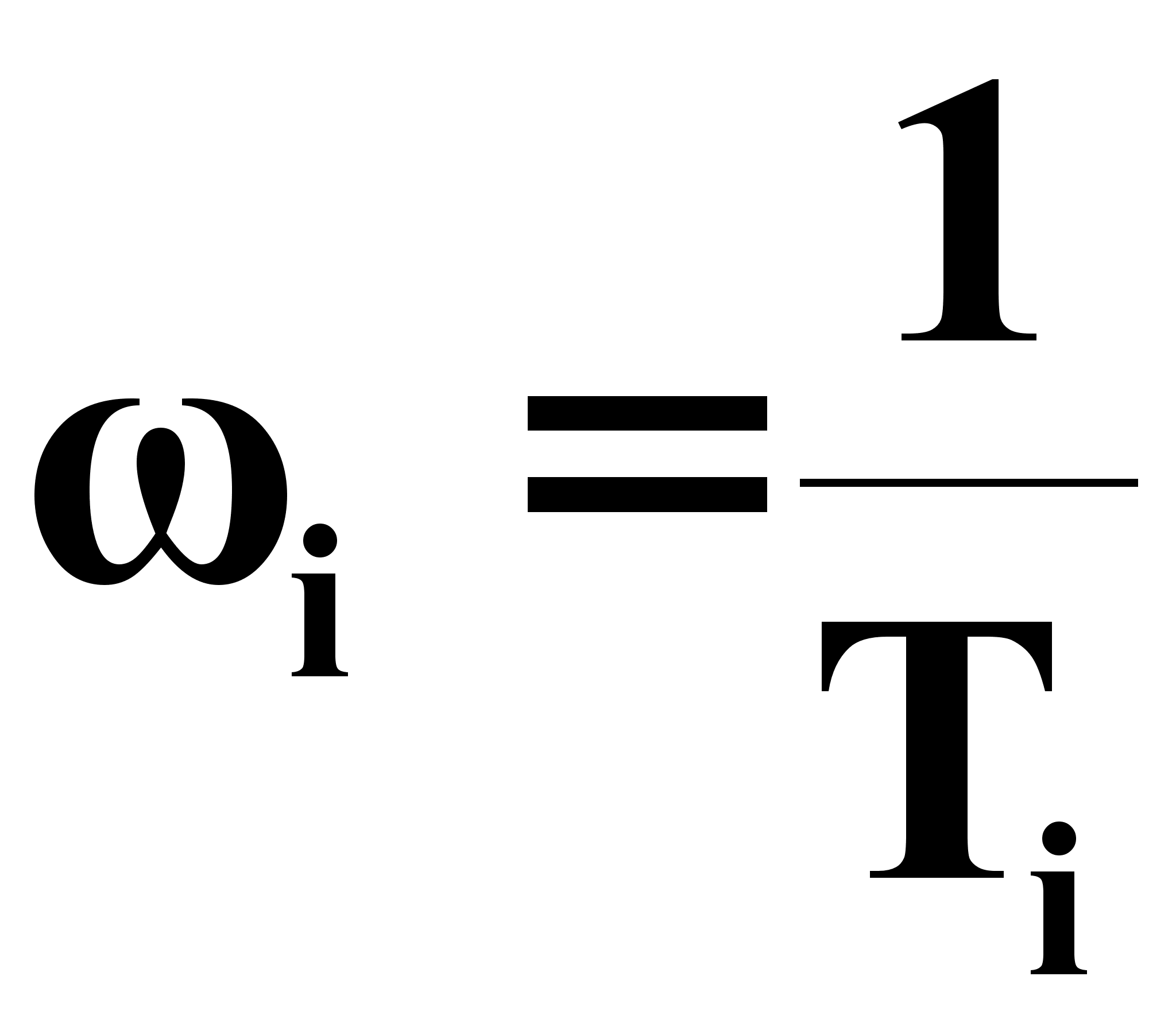(1.26)

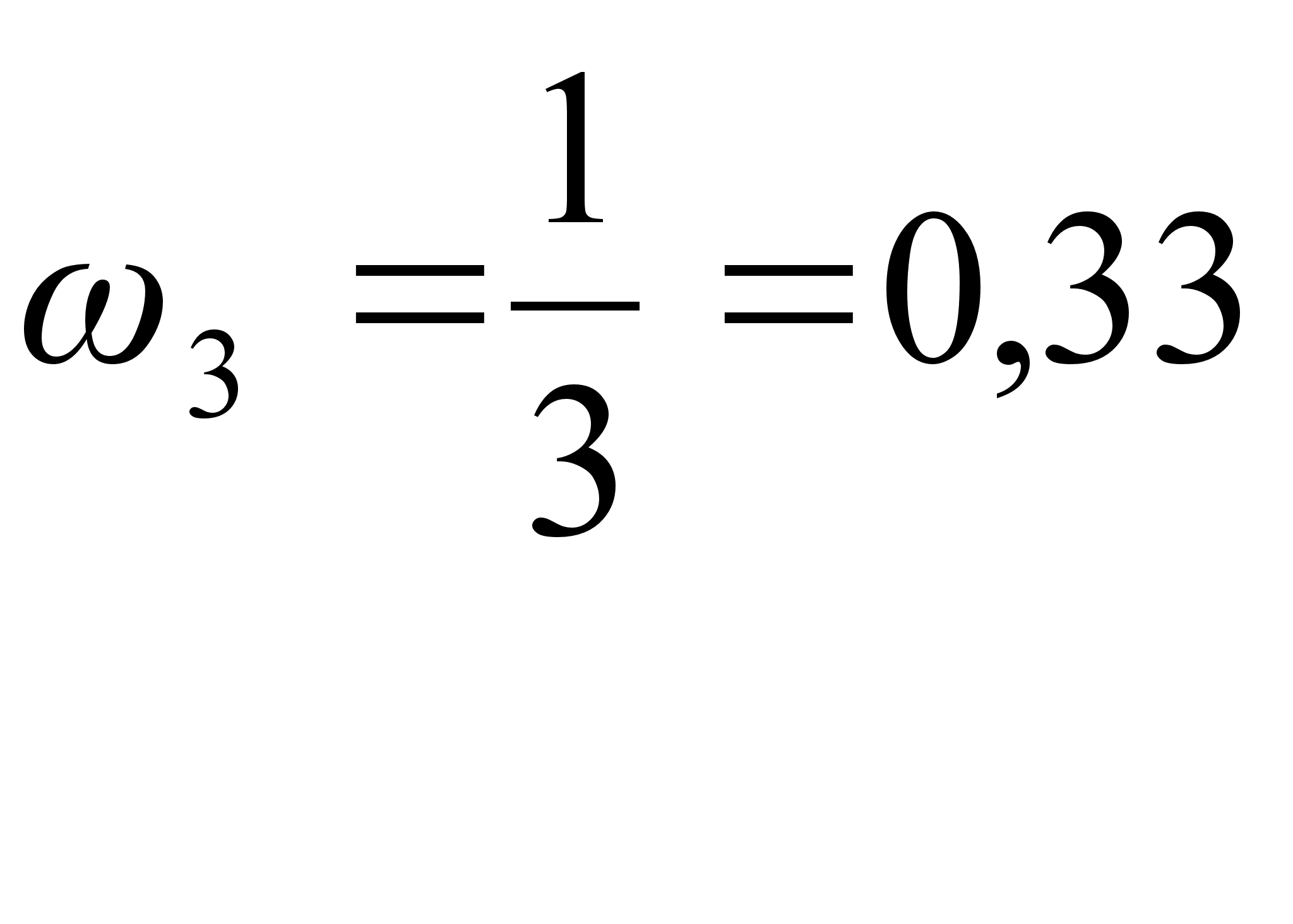
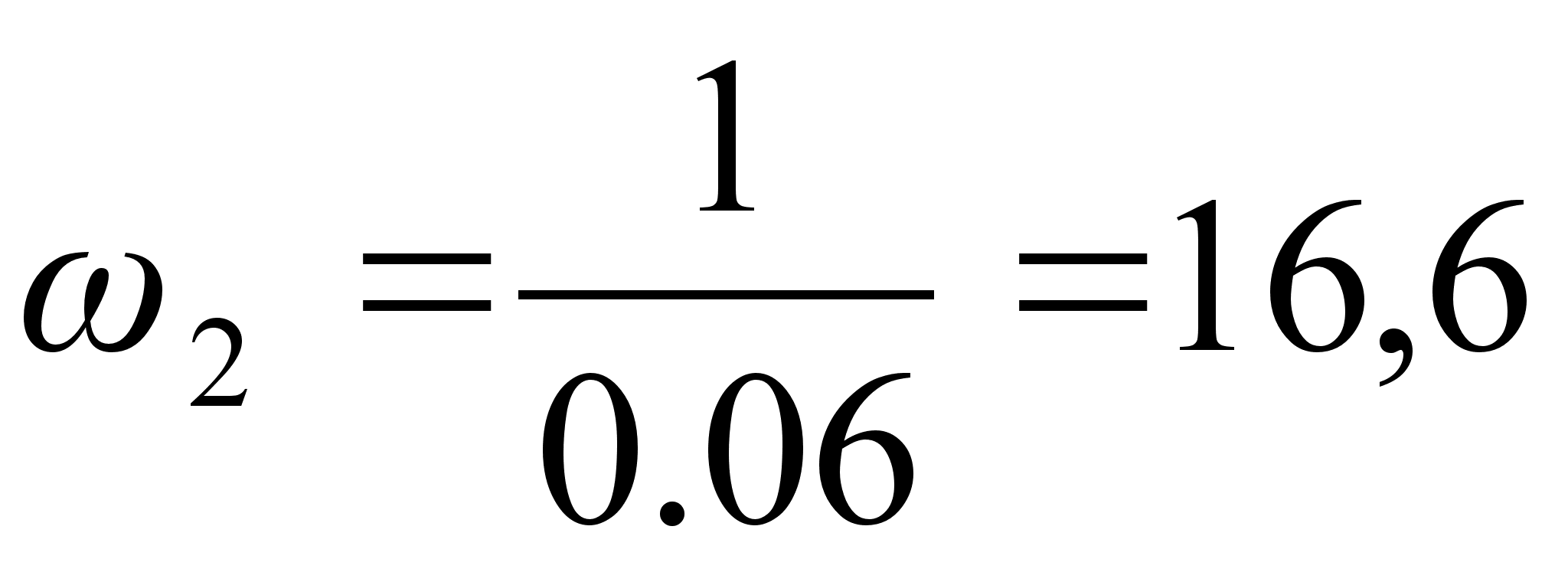
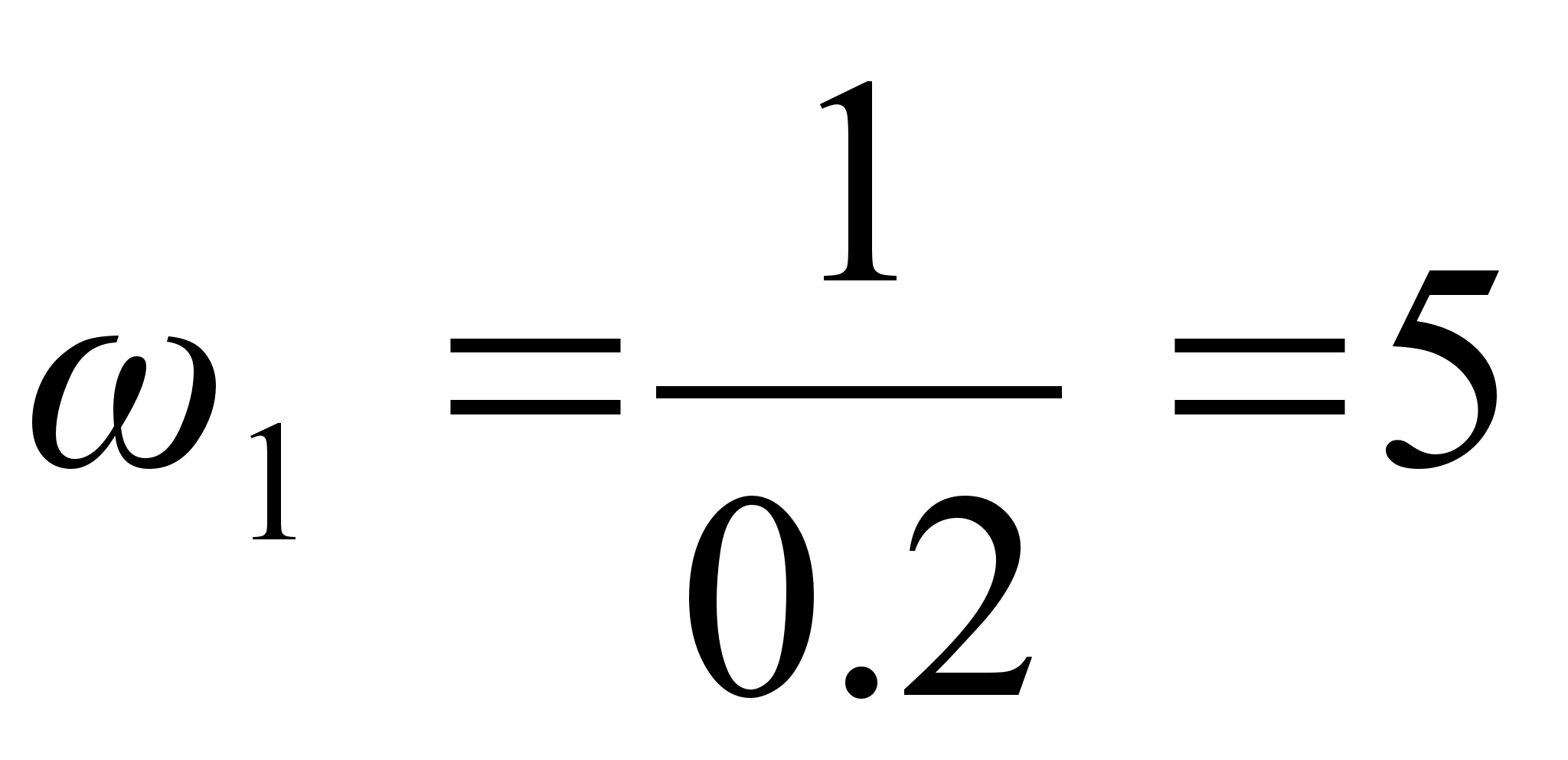
Для построения логарифмических частотных характеристик выбираем следующие масштабы:

-одна декада по оси абсцисс-10 см;

-10 дб по оси ординат-2 см;

-90° по оси ординат-4.5 см.

В этих масштабах откладываем:

-по оси частот-сопрягающие частоты;

-по оси ординат-значение

Через точку проводим прямую с наклоном -40 дб/дек, до частоты сопряжения

на частоте сопрягается следующая прямая с наклоном -20 дб/дек по отношению к предыдущей прямой .Эта прямая проводится до частоты сопряжения

на частоте сопрягается третья прямая с наклоном -20 дб/дек по отношению ко второй прямой.

Третья прямая проводится до частоты сопряжения

Полученная таким образом ломаная кривая представляет собой ЛАЧХ разомкнутой нескорректированной квазистационарной системы, первая прямая проходит с наклоном к оси частот-40 дб/дек;вторая-20 дб/дек;третья0 дб/дек;

четвертая-20 дб/дек.

Фазочастотная характеристика нескорректированной разомкнутой системы строится в тех же координатах согласно выражения (1.24) , где

-первое слагаемое -это прямая, проходящая параллельно оси частот на расстоянии ;

-второе-четвертое слагаемые-тангенсоиды с точками перегиба на частотах сопряжения; в области высоких частот асимптотически приближаются к , а при

Алгебраическая сумма ординат всех четырех характеристик дает фазочастотную характеристику нескорректированной разомкнутой системы..

Для определения запасов устойчивости не скорректированной системы по амплитуде и по фазе необходимо:

-точку пересечения суммарной ФЧХ с линией спроектировать на ЛАЧХ, тогда расстояние проекции этой точки до оси частот будет величиной запаса устойчивости по амплитуде в дб. Если же проекция этой точки окажется выше оси частот, то запаса устойчивости по амплитуде нет.

-проекция частоты среза на суммарную ФЧХ относительно линии определяет величину запаса устойчивости по фазе в градусах, если проекция точки находится выше линии .

Произведенные построения показывают, что рассматриваемая система неустойчива как по амплитуде, так и по фазе. С целью достижения заданных показателей качества строим корректирующее звено.

Похожие работы

Теория искусственного интеллекта

Скачать

139056

8

19

... промышленность и транспортировка нефтепродуктов, энергетика, металлургия, машиностроительная промышленность, медицина, прогнозирование и мониторинг и другие. В начале 60-х годов в рамках исследований по искусственному интеллекту (ИИ) сформировалось самостоятельное направление - экспертные системы (ЭС). В задачу этого направления входит исследование и разработка программ (устройств), использующих ...

Искусственный интеллект

Скачать

36231

4

5

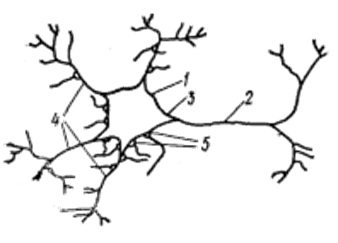
... возможностей ЭВМ и искусства программирования, то есть с тем комплексом научно-технических исследований, которые часто называют компьютерными науками. Второе направление искусственного интеллекта рассматривает данные о нейрофизиологических и психологических механизмах интеллектуальной деятельности и, в более широком плане, разумного поведения человека. Оно стремиться воспроизвести эти механизмы ...

История и тенденции развития искусственного интеллекта

Скачать

64295

0

0

... структуры. PROSPECTOR — экспертная система, созданная для содействия поиску коммерчески оправданных месторождений полезных ископаемых.   2. Перспективы и тенденции развития AI Сообщения об уникальных достижениях специалистов в области искусственного интеллекта (ИИ), суливших невиданные возможности, пропали со страниц научно-популярных изданий много лет назад. Эйфория, связанная с первыми ...

Информационные системы как интеллектуальный инструмент управления предприятием

Скачать

56464

2

2

... в корпоративной системе, обеспечение безопасности корпоративной деятельности – технологических регламентов, систем комплексной информационной безопасности, корпорация «Галактика». Корпоративная система «Галактика», также как и система «1С:Предприятие», – автоматизированная система управления предприятием, но отличие у них в том, что в системе «1С» каждая подсистема имеет свой пользовательский ...