Навигация
1. Очень экономичен.
2. При изменении параметров картинка будет меняться, т. е. каждая формула содержит не одну, а сотни картинок, что позволяет создавать двигающиеся изображение. Недостатком векторного способа является сложность некоторых формул для построения фотореалистичного изображения. Пример: рекламное изображение всё-таки до сих пор не создают полного эф
3. фекта реальности и больше похожи на мультипликацию, но развивающиеся компьютерные технологии очень скоро приведут к тому, что эти изображения будут полностью неотличимы от реальных. Это позволит создавать кинофильмы на компьютере.
Основные понятия и операции формальной логики.
Логика¾наука, которая с помощью формальных правил определяет истинность или ложность высказывания. При создании компьютеров его элементы получили название логических элементов.
Элементарные логические функции.
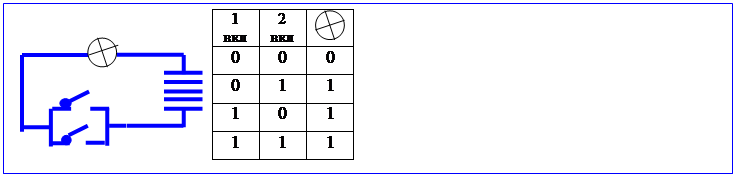
Это функции, которые могут принимать значение 0 или 1. Из трёх и, или, не. Наиболее просто смысл логических функций объясняется с помощью электронной системы выключателя. Функция И
|
П
П
П
|
П
88П 88
Функция ИЛИ
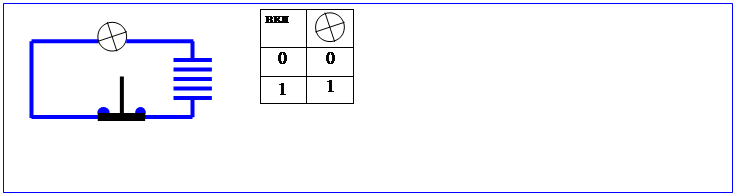
Функция НЕ
Помимо простых функций И, ИЛИ, НЕ существуют ещё так называемые сложные функции, то есть сочетание простых функций И, ИЛИ, НЕ.
Логические элементы компьютера.
Компьютер состоит из миллионов элементов, связанных между собой и взаимодействующих во время его работы. Каждый элемент выполняет какую-либо операцию над двоичным разрядом.
Машинные элементы делятся на логические, запоминающие и вспомогательные. Из логических элементов состоят операционные схемы, обеспечивающих выполнение арифметических и логических операций над цепочками двоичных разрядов¾машинными символами. Запоминающие элементы предназначаются для хранения информации. Вспомогательные элементы предназначаются для формирования стандартных сигналов и согласования работы операционных схем.
Переменные и функции, принимающие значение 0 или 1 носят название логических или булевских по имени английского математика и логика Джорджа Буля (1815-1864), является создателем современной символической логики. Подробным изучением булевских функций занимается область математической логики или исчислением высказываний. Каждому высказыванию в соответствии значение её функции, истинности, равное 1, когда высказывание истинно и 0, когда оно ложно.
Логическая функция И.
9
Логическая функция И от двух аргументов определяется таблицей.
 | |||
 | |||
Этим значением
обозначается
Конъюнкция
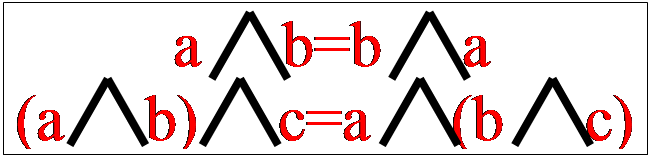
Легко видеть, что логическая функция И совпадает с произведением аргументов. Поэтому её называют также логическим умножением. Ещё одно название¾Конъюнкция. Нетрудно определить функцию И для любого конечного числа аргументов. Она равна 1 тогда и только тогда, когда все сомножители равны 1, как и должно быть для произведения. Логическое умножение подчиняется переместительному и сочетательному законам.
-2+3=3+2 Коммутативны 7-3=3-7 Не коммутативны
7*3=3*7
(3+2)+7=3+(2+7)
5+7=3+9
(3*7)*2=3*(7*2)
И
 |  |  |  | ||||||
 | |||||||||
Логическая функция ИЛИ
Логическая функция ИЛИ от двух аргументов определяется таблицей. Её называют логическим сложением или Дизъюнкцией. Следует помнить, что логическая сумма отличается от арифметической суммы. Логическая сумма нескольких слагаемых ровна 0 тогда и только тогда, когда все слагаемые равны 0. Эта операция также подчиняется переместительному и сочетательному законам.
Дизъюнкция
10
Логическая функция НЕ.
Логическая функция НЕ (отрицание) зависит от одного аргумента и определяется таблицей. Функция НЕ обозначается горизонтальной чертой над аргументом или особым знаком.
Логические выражения и их образование.
Подобно арифметическим операциям, логические операции имеют различное «Старшинство», что отражается на порядке их выполнения в выражениях, содержащих символы различных операций: прежде всего выполняются операции НЕ, затем И и только потом ИЛИ. Здесь наблюдается полная аналогия с алгебраическими выражениями. При вычислении по формуле а2*b2+c2 сначала выполняется возведение в степень, затем умножение и тол ько потом сложение аналогично формуле.
Сначала выполняются отрицания, затем конъюнкция, а потом дизъюнкция. В тех случаях, когда нужно изменить этот порядок применяются круглые скобки. Правила их применения ничем не отличаются от правил применения скобок в алгебраической формуле.
Логические выражения и их преобразование.
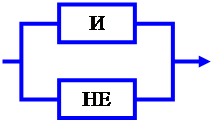
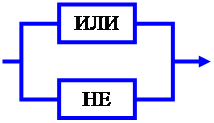
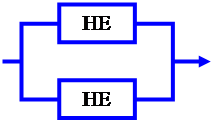
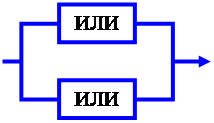
Любую функцию трёх и более аргументов можно представить формулой, в которой в которой фигурируют элементарные логические функции. Например, функция три аргумента представленная таблицей.
| Аргументы | Функ. | ||
| а | b | c | z |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
|
| 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
1 | ||||||
 | ||||||
 | ||||||
 | ||||||
 | ||||||
 | ||||||
 | ||||||
 | ||||||
 | ||||||
 | ||||||
 |  | |||||
|
| b | c | d | - | ||
|
| 0 | 0 | 0 | 0 | ||
|
| 0 | 0 | 1 | 0 | ||
|
| 0 | 1 | 0 | 0 | ||
| 0 | 0 | 1 | 1 | 0 | ||
|
| 1 | 0 | 0 | 0 | ||
| 0 | 1 | 0 | 1 | 0 | ||
| 0 | 1 | 1 | 0 | 0 | ||
|
| 1 | 1 | 1 | 0 | ||
| 1 | 0 | 0 | 0 | 0 | ||
| 1 | 0 | 0 | 1 | 0 | ||
| 0 | 1 | 0 | 0 | ||
| 1 | 1 | 0 | 0 | 0 | ||
|
| 1 | 0 | 1 | 0 | ||
| 1 | 1 | 1 | 0 | 0 | ||
|
| 1 | 1 | 1 | 1 |
a
0
0
0
0
1
1 |  | ||
Преобразование информации.
Преобразованием или перекодированием информации называют её запись с помощью других знаков. Пример:
Перевести с одного языка на другой, записать устную речь, чтение вслух, описание словами какого-либо рисунка, экранизации романа и др. Проблема, которая при этом возникает:
Иногда происходит потеря части информации из-за несоответствия кодов (при переводе с русского языка на английский невозможна точность перевода из-за отсутствия эквивалентов, т. е. в русском языке есть слова непереводимые на английский).
Наиболее точное преобразование информации происходит при перекодирование на уровне элементов информации. Например, азбука Морзе, в которой каждому знаку соответствует сочетание точек и тире. На таком принципе построено применение телеграфных кодов, кодировка в компьютере. Для того, чтобы унифицировать (сделать) одинаковое кодирование на всех компьютерах была принята таблица кодов ASCLL-код. Пример:
ASCLL-код ¾ буква А-41, а-61, О-30, 1-31.
Всего возможно закодировать 256 разных символов. Можно ввести любой из этих символов, даже если его нет на клавиатуре, нажав на клавишу ALT и удерживая её набрать на числовой клавиатуре ASCLL –код символа.
Шифрование.
Шифрование это частный случай кодирования, при котором обеспечивается невозможность прочтения информации теми, кто не владеет ключом к расшифровке. Шифровать можно как текстовую, так и любую другую информацию, т. е. изображение, звук, видео. Шифруют специальную военную информацию, государственную информацию, коммерческую информацию, а также частную.
Способы шифрования:
Похожие работы
... , одни из которых осуществляют финансово-хозяйственную деятельность, другие осуществляют управление этой деятельностью. 2. Прямые и обратные потоки хозяйственной информации. Понятие и схема функционирования экономической информационной системы, информационный процесс экономического агента В рамках системы управления циркулируют информационные потоки, они могут быть как прямые и обратные. ...
... , связанный с формированием представлений о системно-информационном подходе к анализу окружающего мира, о роли информации в управлении, специфике самоуправляемых систем, общей закономерности информационных процессов в системах различной природы. Основой мировоззрения, главным его компонентом является научная картина мира, рассматриваемая как высший уровень систематизации и обобщения научных ...
... этих трёх условий приводит прежде всего к тому, что система становится информационно обособленной, у системы (субъекта) формируется своё семантическое пространство, сфера внутренних информационных процессов. Это основное инвариантное свойство любого субъекта. Понятие “семантического поля”, введенное В.В. Налимовым [4-7], предполагает соотнесение смыслов с числовой осью — линейным континуумом ...
... исключительно велика. Без него, без обмена информацией между людьми было бы невозможным возникновение и развитие общества. 1. Информационные процессы как ядро информационной теории 1.1. Понятие и классификация информационных процессов Процессы, связанные с поиском, хранением, передачей, обработкой и использованием информации, называются информационными процессами. Теперь остановимся ...
0 комментариев